[백준] 7812번 : 중앙 트리

🔗 문제 링크

https://www.acmicpc.net/problem/7812

---

✍️ 문제 풀이

해당 문제는 트리 자료구조 형식의 문제이다. 모든 정점에서 한 번씩 DFS를 돌려 다른 정점까지 이르는 비용 합을 구할 수 있지만, 이 경우 정점 개수가 많아지면 시간 초과가 발생할 수 밖에 없다. 때문에 DP를 사용하여 중복되는 과정을 저장해가며 풀어야 한다.

1) 각 노드 v에 대한 pair(인접 노드, v와 인접 노드 간 거리)들의 벡터를 저장하는 벡터 edges,

각 노드 v에 대한 tuple(인접 노드, 인접 노드를 루트로 하는 서브트리에 있는 모든 노드들과 현재 노드 사이 거리의 총합, 인접 노드 서브트리의 노드 개수)를 저장하는 벡터를 저장하는 벡터 dp를 선언한다.

그리고 각 노드 v의 인접 노드를 루트로 하는 서브트리에 대한 데이터가 dp에서 어떤 인덱스에 저장되어 있는지 저장하는 벡터 dpIndex를 선언한다.

2) 데이터를 입력 받아 각 노드에 어떤 노드가 인접해있는지, 그 노드와 거리는 얼마인지 edges에 저장하고, 이 때 인접 노드 개수만큼 각 노드에 대한 dpIndex의 크기도 늘려주며 -1로 초기화한다.

3) 각 노드에서 시작하는 DFS()를 돌려 각 노드부터 다른 노드들까지의 거리 합을 구한다.

• 현재 노드와 인접한 노드들을 차례대로 확인하며 방문하지 않은 노드로 진출한다.
  • 만약 인접 노드에 대한 데이터가 dp에 저장되어있지 않은 경우 (== dpIndex 값이 -1일 때)
    • 거리를 누적시키고, 인접 노드로 시작하는 DFS()를 실행한다.
    • 현재 노드에 대한 인접 노드 데이터 [인접노드 번호, (인접 노드를 루트로 하는 서브트리에 있는 모든 노드들과 v 사이 거리의 총합) - (현재 노드까지 누적 거리 * 인접노드 서브트리의 노드 개수), 인접노드 서브트리의 노드 개수]를 dp에 저장한다.
    • 인접노드 데이터가 dp의 어떤 인덱스에 저장되어있는지 dpIndex에 저장한다.
  • 인접 노드에 대한 데이터가 이미 dp에 저장되어 있는 경우
    • dp에 저장되어있는 데이터를 꺼내서 거리에 누적시킨다.

4) 위 DFS()가 끝나면 나오는 각 노드부터 다른 노드들까지의 거리 합 중 가장 작은 값을 출력한다.

---

🔎 부가 설명

글로 쓰니 이해가 잘 안 되는 것 같아서 문제에 있는 예시에 대해 그림으로 나타내보겠다.

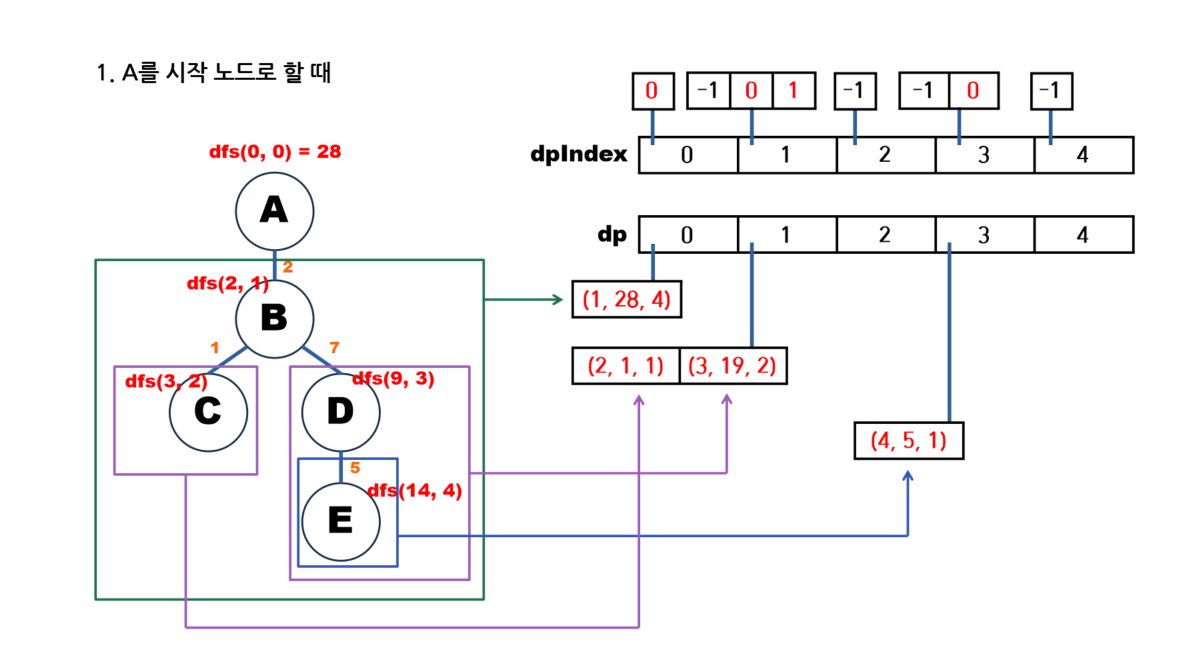
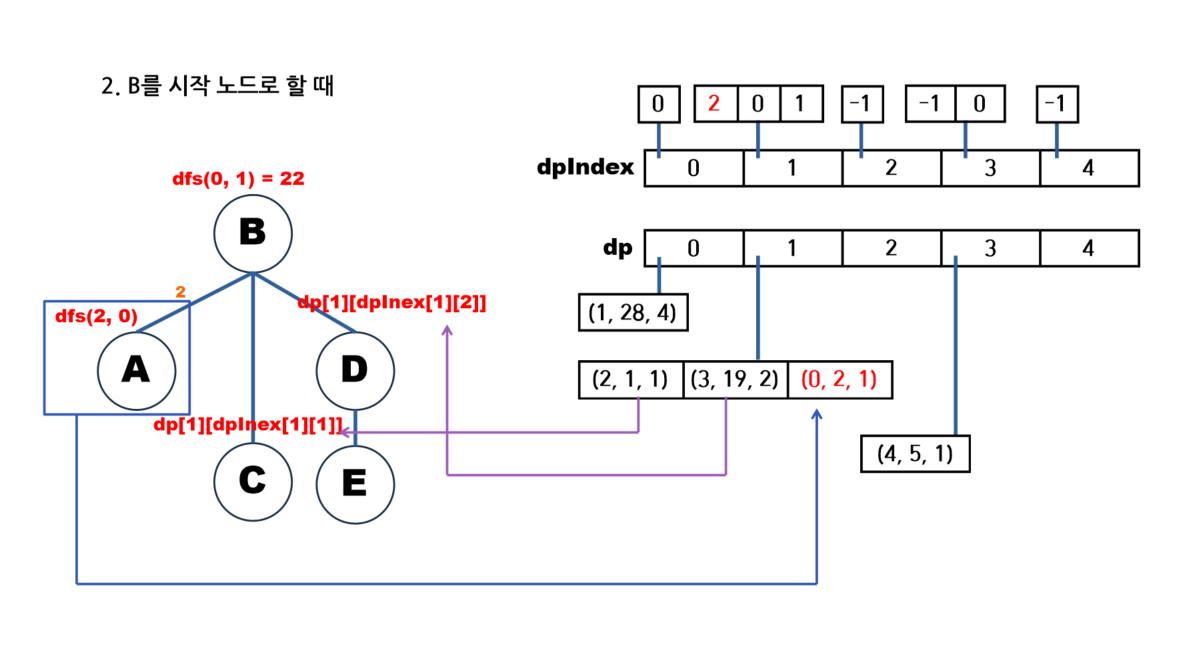
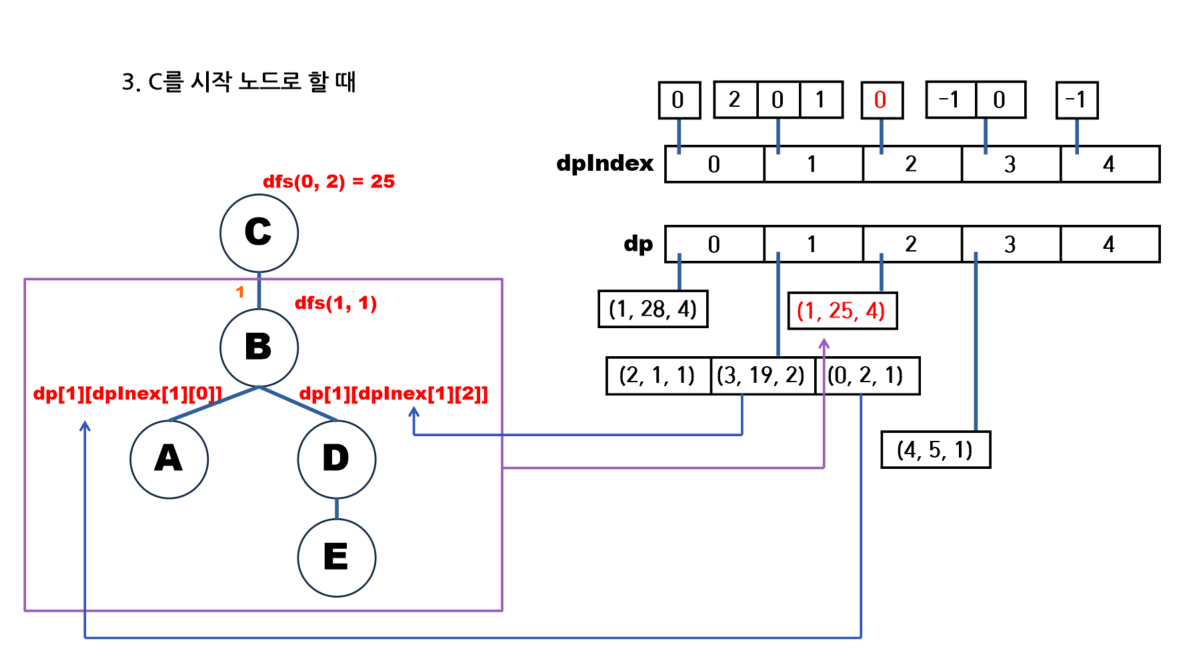
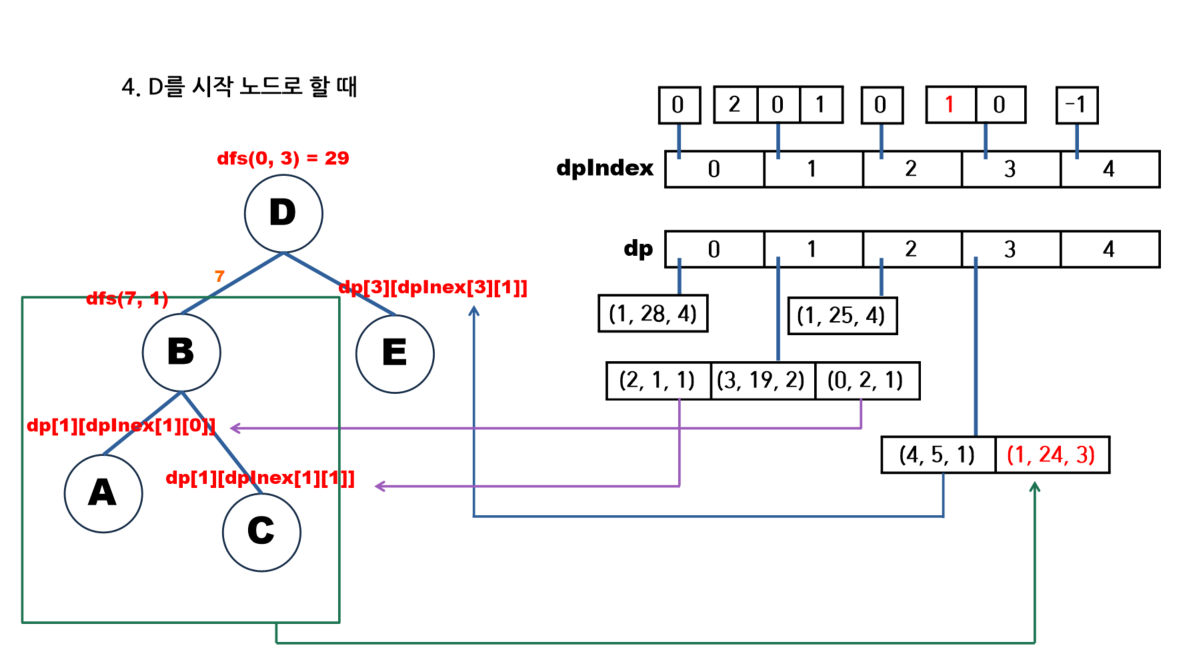
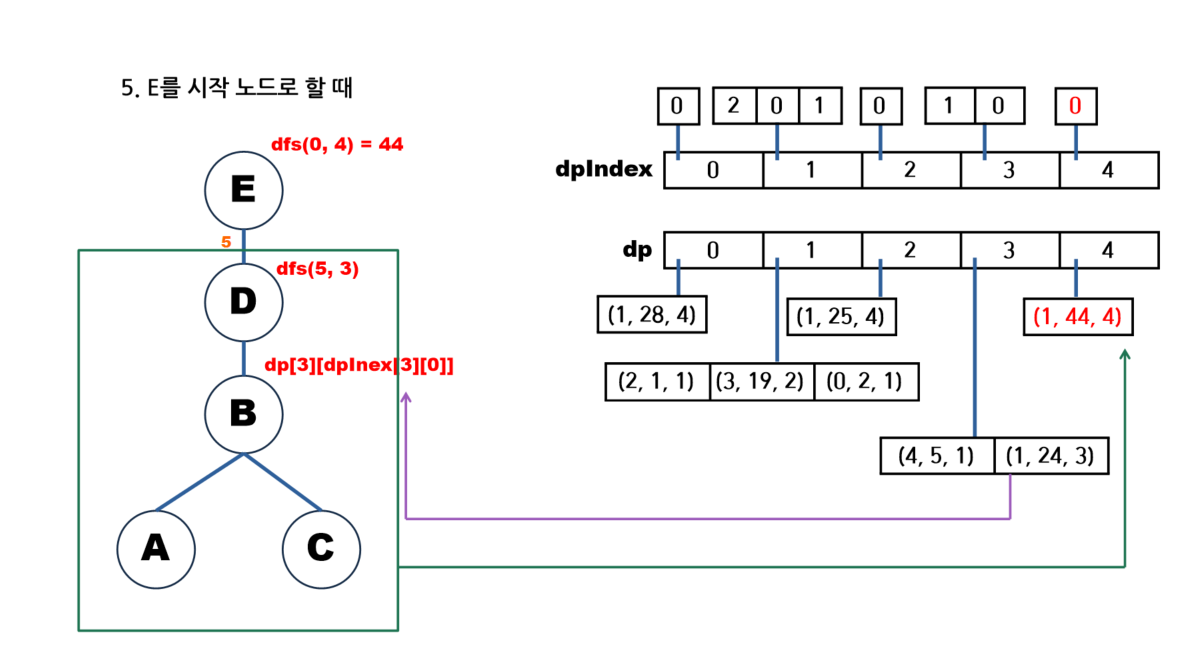
🖥️ 풀이 코드

#include <iostream>
#include <vector>
#include <algorithm>
#include <tuple>

using namespace std;
typedef pair<int, int> pii;
typedef pair<long long, int> pli;
typedef tuple<int, long long, int> tili;

vector<vector<pii>> edges;   // 각 노드 v에 대해 (인접 노드, v와의 거리)를 저장하는 pair들의 벡터들을 저장하는 벡터
vector<vector<tili>> dp;     // 각 노드 v에 대해 (인접 노드, 인접 노드를 루트로 하는 서브트리에 있는 모든 노드들과 v 사이 거리의 총합, v 아래로 존재하는 노드 개수)
vector<vector<int>> dpIndex;
vector<bool> visited;

int n, a, b, w;
long long minDist;

pli DFS(long long distance, int currentNode)
{
    long long result = distance;
    int nodeCount = 0;
    visited[currentNode] = true;

    for (int i = 0; i < edges[currentNode].size(); i++)
    {
        int childNode = edges[currentNode][i].first;

        if (visited[childNode] == false)
        {
            visited[childNode] = true;
            if (dpIndex[currentNode][i] == -1)
            {
                pli tmp = DFS(distance + edges[currentNode][i].second, childNode);
                result += tmp.first;
                nodeCount += tmp.second + 1;
                dp[currentNode].push_back(tili(childNode, tmp.first - ((long long)tmp.second + 1) * distance, tmp.second + 1));
                dpIndex[currentNode][i] = dp[currentNode].size() - 1;
            }
            else
            {
                tili dpData = dp[currentNode][dpIndex[currentNode][i]];
                nodeCount += get<2>(dpData);
                result += get<1>(dpData) + (long long)get<2>(dpData) * distance;
            }
            visited[childNode] = false;
        }
    }
    return pli(result, nodeCount);
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(); cout.tie();

    while (true)
    {
        cin >> n;
        if (n == 0)
            return 0;

        edges.clear();
        edges.resize(n);
        dp.clear();
        dp.resize(n);
        visited.clear();
        visited.assign(n, false);
        dpIndex.clear();
        dpIndex.resize(n);

        for (int i = 0; i < n - 1; i++)
        {
            cin >> a >> b >> w;

            edges[a].push_back(pii(b, w));
            edges[b].push_back(pii(a, w));
            dpIndex[a].push_back(-1);
            dpIndex[b].push_back(-1);
        }

        minDist = DFS(0, 0).first;
        for (int i = 0; i < n; i++)
        {
            long long dfs = DFS(0, i).first;

            if (dfs < minDist)
                minDist = dfs;

            visited.assign(n, false);
        }
        cout << minDist << '\n';
    }
}