[백준] 11054번 : 가장 긴 바이토닉 부분 수열

🔗 문제 링크

https://www.acmicpc.net/problem/11054

✍️ 문제 풀이

해당 문제는 다이나믹 프로그래밍 문제로, LIS 문제를 응용하여 푸는 문제이다.
최장 바이토닉 부분 수열은 특정 인덱스에서의 최장 증가 수열과 최장 감소 수열을 합친 것의 최대값이라고 볼 수 있다.
ex. 수열 {50 10 20 30 25 20}의 최장 바이토닉 부분 수열은

• 인덱스 4에서의 최장 증가 수열인 {10 20 30}
• 인덱스 4에서의 최장 감소 수열인 {30 25 20}
• 위 둘을 합친 {10 20 30 25 20} 이 최장 바이토닉 부분 수열이 된다.

1) nums에 수열을 입력받아 저장하고, nums2에 입력 받은 수열을 역순으로 저장한다.

2) 배열 dp1, dp2를 선언하고, 각각을 차례대로 갱신한다.

• dp1[i] : i 번째 수까지 있을 때, 수열의 부분 수열 중 최장 증가 수열의 길이
• dp2[i] : i 번째 수까지 있을 때, 역순 수열의 부분 수열 중 최장 증가 수열의 길이
  == 수열의 부분 수열 중 최장 감소 수열의 길이
  

3) i가 0 ~ n일 때

• (dp1[i]와 dp2[n - i + 1]의 합 - 1)을 구해 maxValue와 비교한다.

  • -1을 해주는 이유 : 가운데 수가 중복되어 더해지기 때문이다.
    ex. 인덱스 i에서의 최장 증가 부분 수열이 {10 20 30} 이고, 최장 감소 부분 수열이 {30 25 20} 일 때 최장 바이토닉 부분 수열은 {10 20 30 25 20}인데, 이 때 30이 중복되기 때문에 1을 빼준다.

• 만약 위 수가 maxValue보다 크다면 maxValue를 위 수로 갱신한다.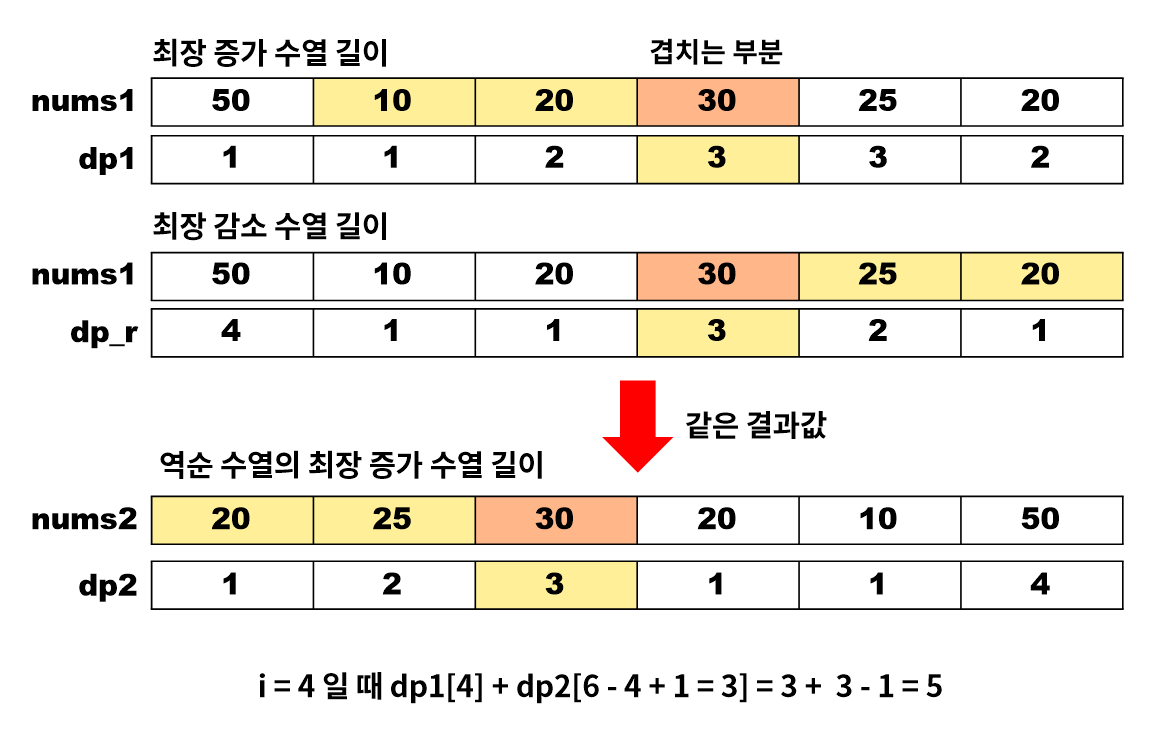

  

4) 최종적으로 maxValue에 최장 바이토닉 부분 수열의 길이가 저장된다.

🖥️ 풀이 코드

#include <iostream>
#include <algorithm>
using namespace std;

int nums[1001];
int nums2[1001];
int dp1[1001];		
int dp2[1001];

int solution(int n)
{
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j < i; j++)
		{
			if (nums[i] > nums[j] && dp1[j] + 1 > dp1[i])
				dp1[i] = dp1[j] + 1;

			if (nums2[i] > nums2[j] && dp2[j] + 1 > dp2[i])
				dp2[i] = dp2[j] + 1;
		}
	}

	int maxValue = 0;
	for (int i = 0; i <= n; i++)
	{
		int sum = dp1[i] + dp2[n - i + 1] - 1;
		if (maxValue < sum)
			maxValue = sum;
	}
	return maxValue;
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);

	int n;
	cin >> n;

	for (int i = 1; i <= n; i++)
	{
		cin >> nums[i];
		nums2[n - i + 1] = nums[i];
		dp1[i] = 1;
		dp2[i] = 1;
	}

	cout << solution(n);
}