[5주차]
TIL
차량 모델 - 종방향 모델
-
등판 성능 (Dynamic Axle Load)
-
가속 성능 (Acceleration)
-
제동 성능 (Braking)
-
주행 저항 (Driving Resistance)
차량 모델 - 횡방향 모델
-
저속 선회 (Kinematic bicycle model)
-
배경 지식 (비관성좌표계, 클로소이드 도로모델, 최소제곱해 (fitting), Tire force)
-
(정상상태) 고속 선회 (Dynamic bicycle model - tire slip angle 존재)
차량 제어
-
종방향 제어 (ACC: Speed control, Spacing control)
-
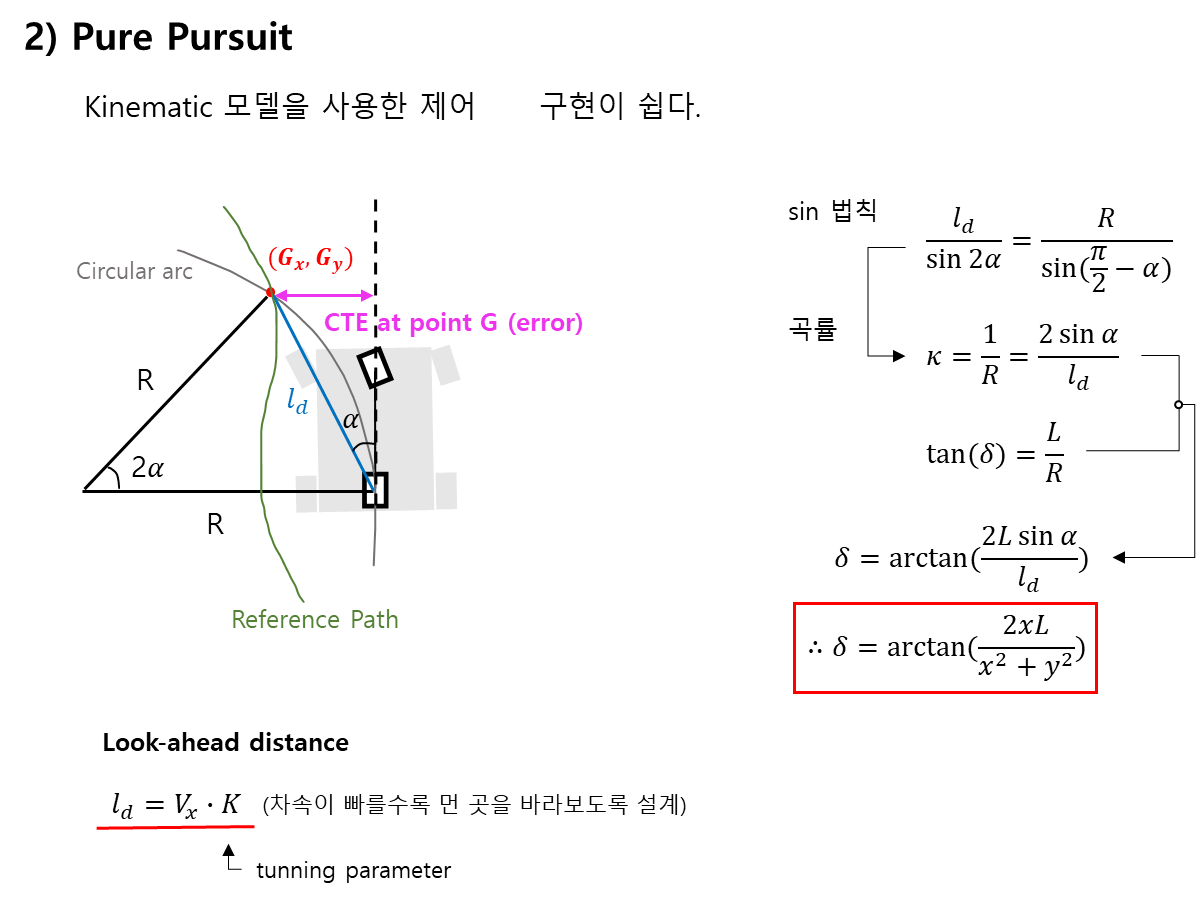
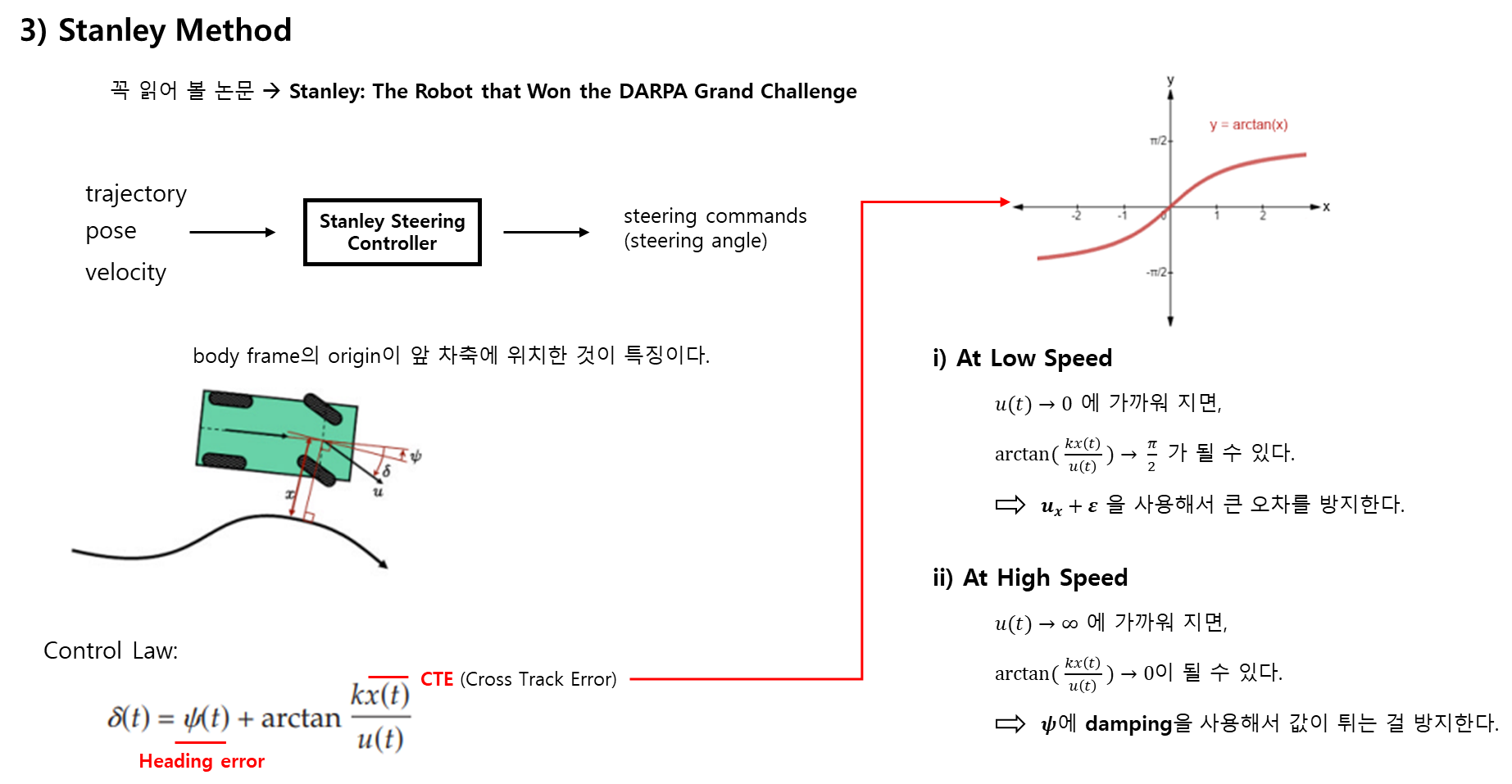
횡방향 제어 (Error term dynamic model, Pure pursuite, Stanley method)
5주차 skill set
1) Longitudinal Vehicle Modeling
2) Lateral Vehicle Dynamics
3) Vehicle Control (longitudinal & lateral)
학습내용
[1] Longitudinal Vehicle model
1. Dynamic Axle Load
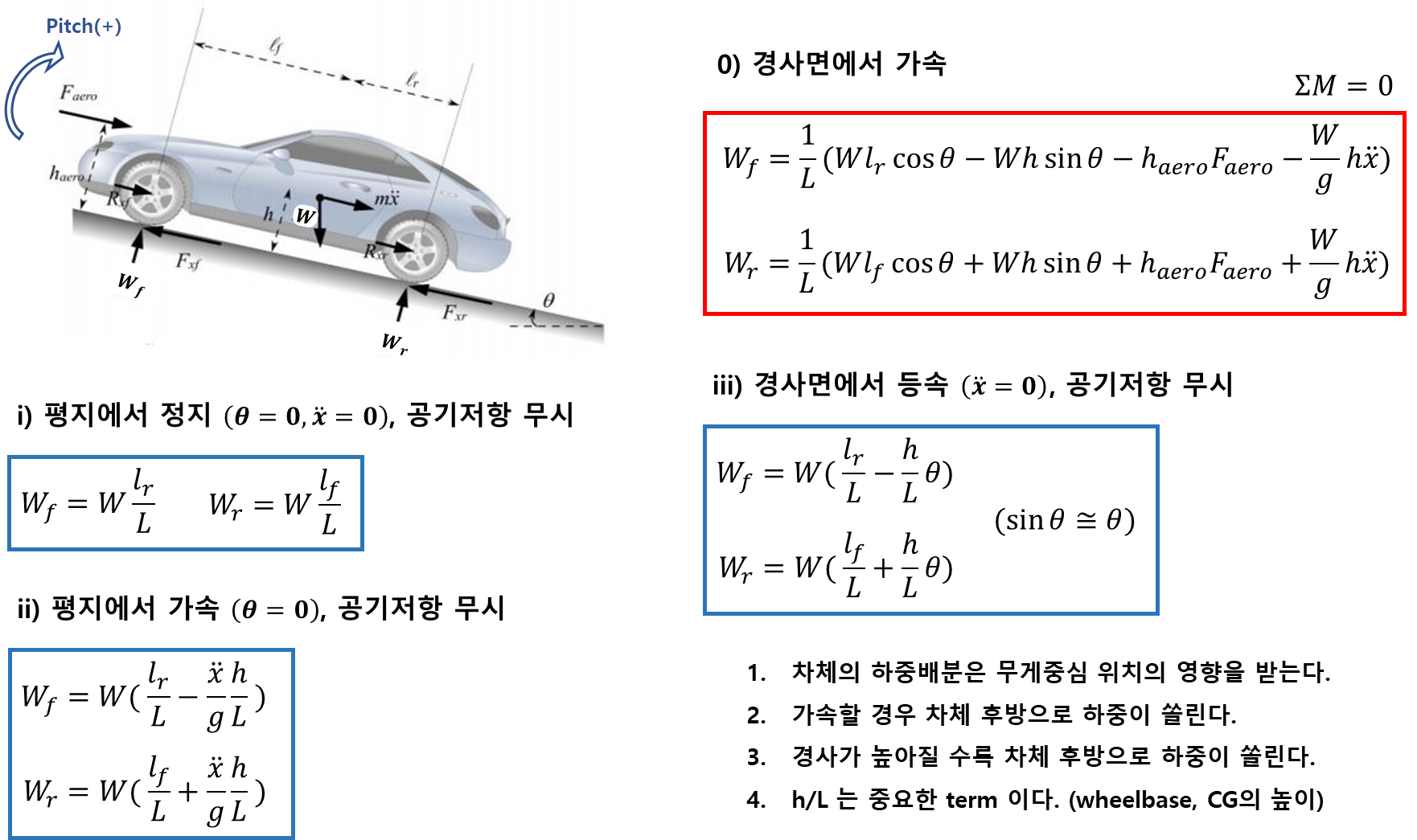
- 이 모델은 longitudinal model에서 가속 및 제동 성능을 표현하고 이해하는데 사용된다.
2. Acceleration
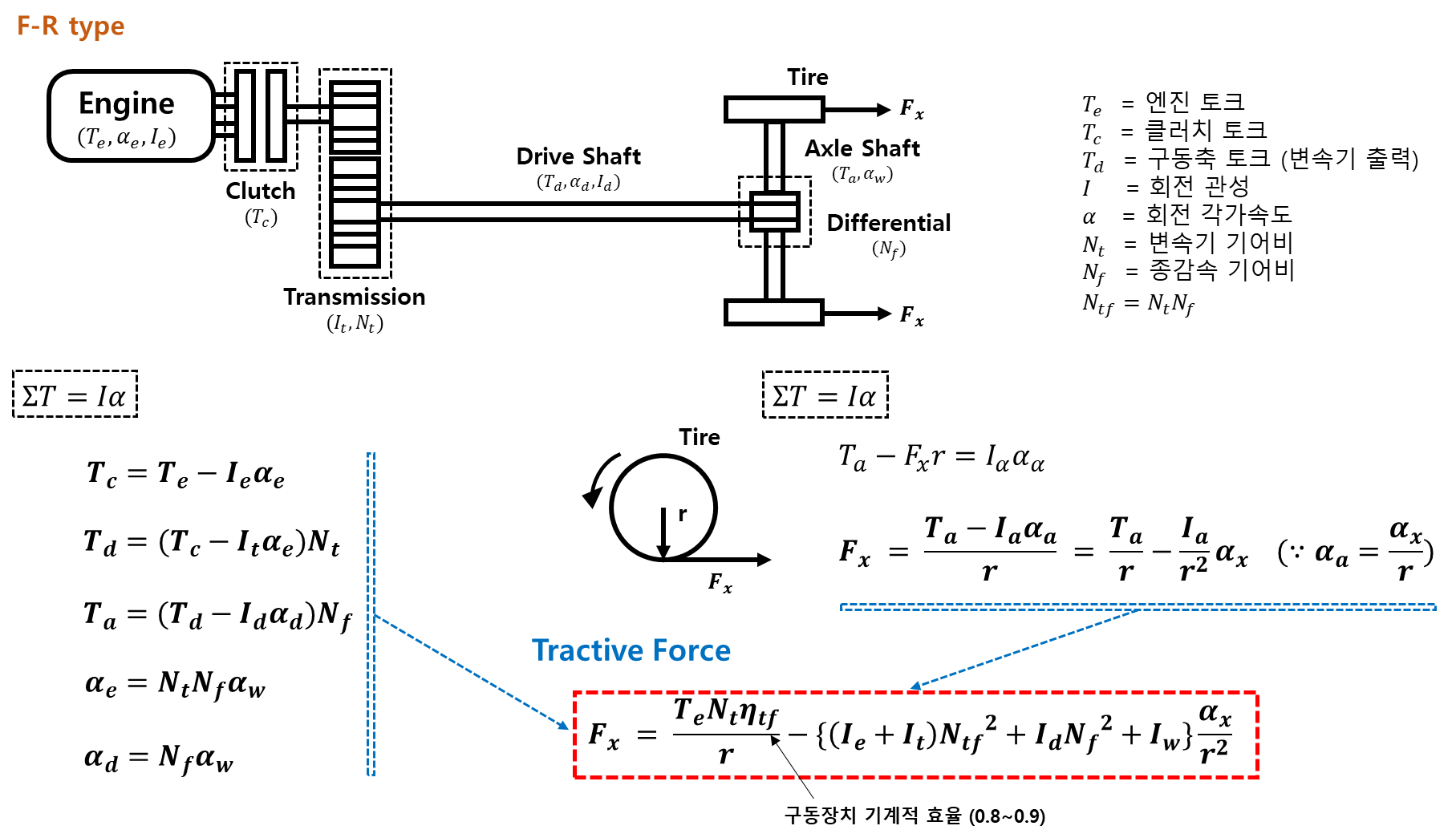
-
Traction Force의 첫 번째 항은 "(엔진토크) x (기어비) x (기계적효율) / 타이어 반경" 이다.
- 타이어가 작을수록, 엔진 토크와 기어비가 클 수록 차량의 추진력이 좋다는 것을 알 수 있다.
-
두 번째 항은 동력 전달 과정에서 회전 관성으로 인해 발생하는 동력 손실이다.
- 이를 감소시키기 위해 각 요소별 질량을 줄이는 등 회전 관성을 최소화 해야하지만, 쉽지 않다.
- 여기서 타이어의 반지름이 제곱 항으로 들어가 있어, 타이어가 너무 작으면 오히려 추진력에 부정적인 영향을 끼친다는 것을 알 수 있다.
-
하지만 가장 중요한 것은 Traction Force는 당연히 타이어의 마찰력을 넘을 수 없다는 것이다. F_xf <= μW_f , F_xr <= μW_r
-
이외에 dynamic axle load model 에서 회전 관성을 분리하여 고려했을 때의 유효 질량(Effective mass), 수동 및 자동 변속(MT/AT)에서 Nt에 따른 엔진 최대 출력 곡선 등에 대한 추가적인 내용은 필요하면 학습 하는 걸로~
3. Braking
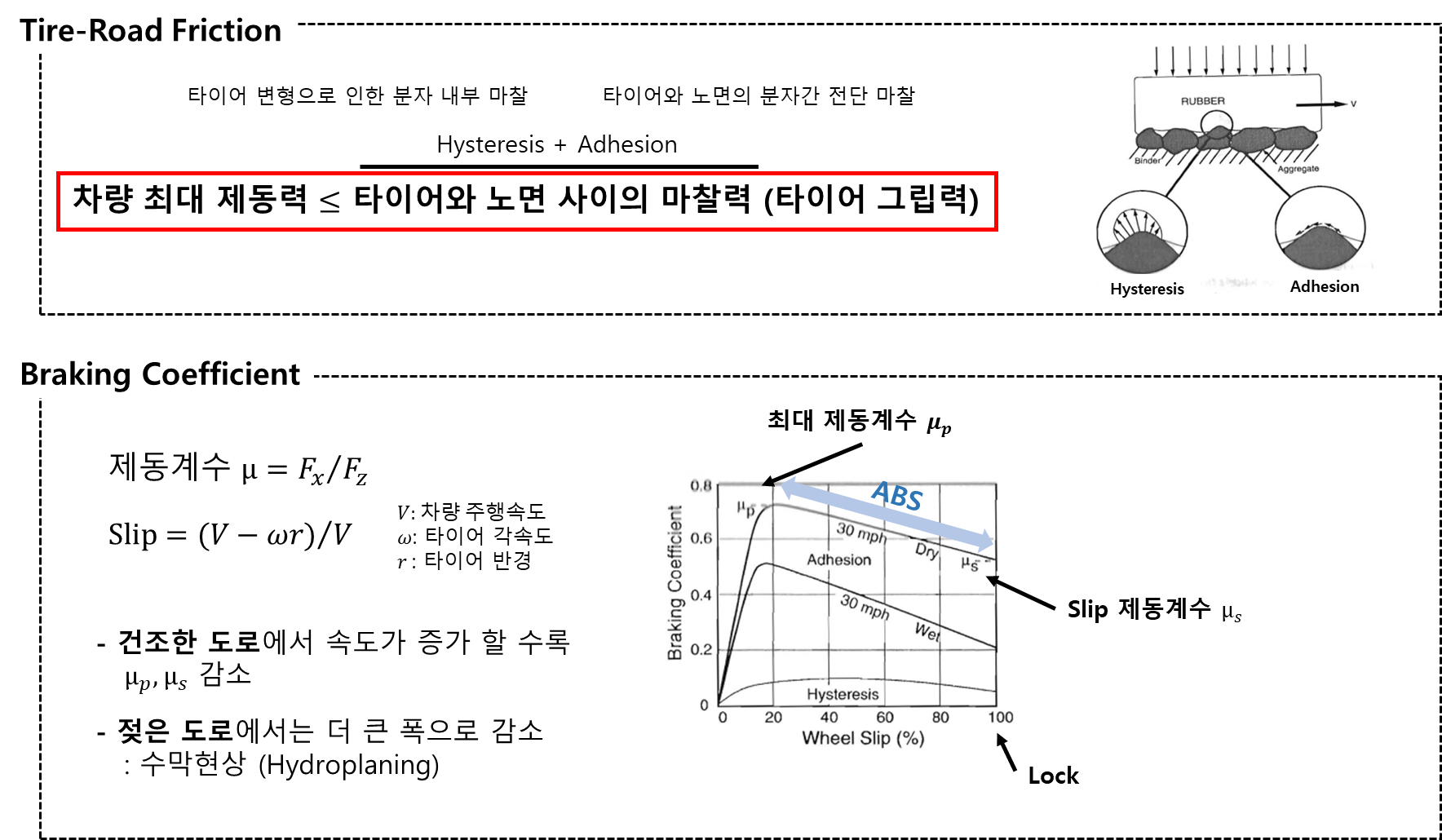
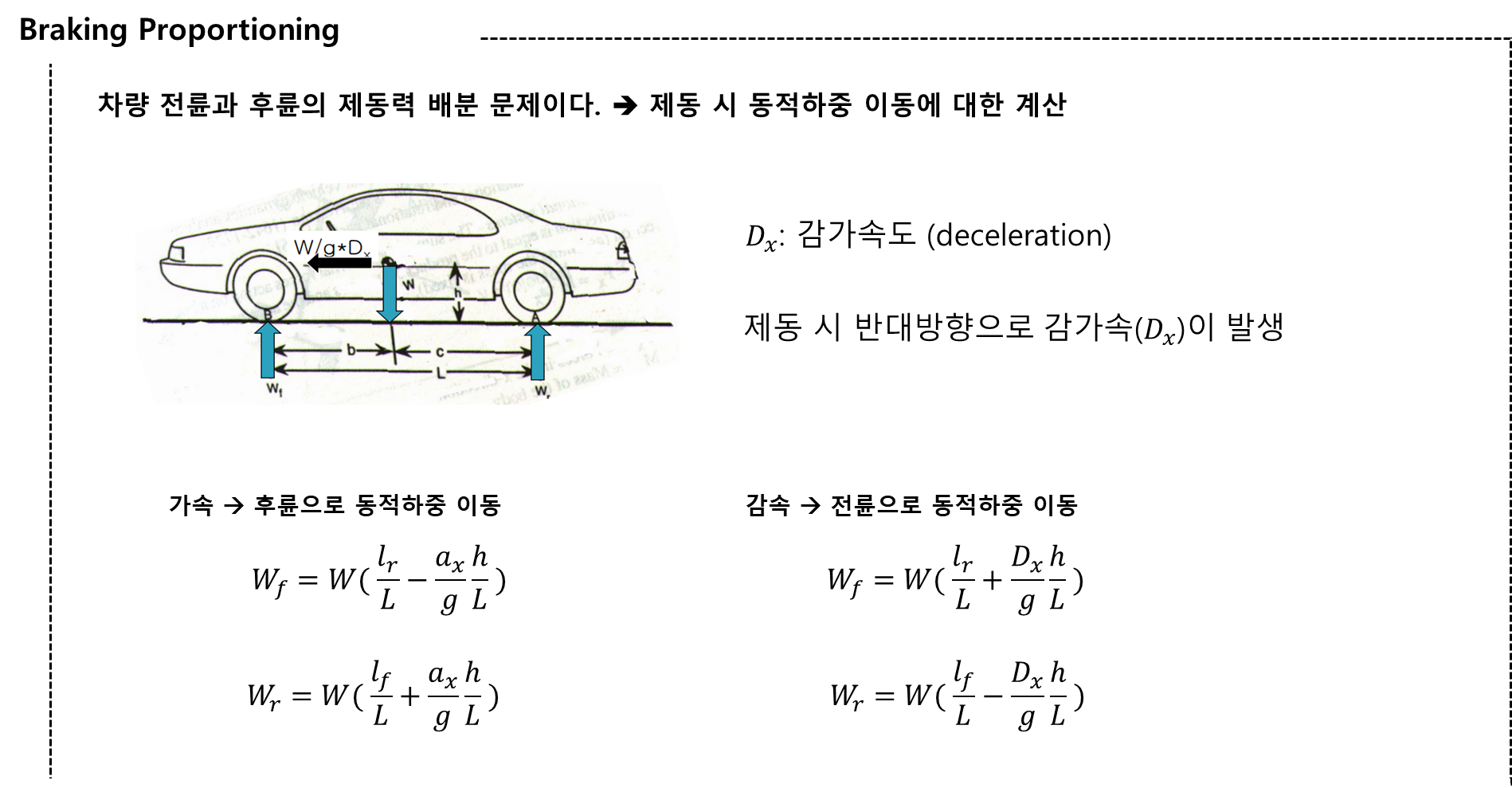
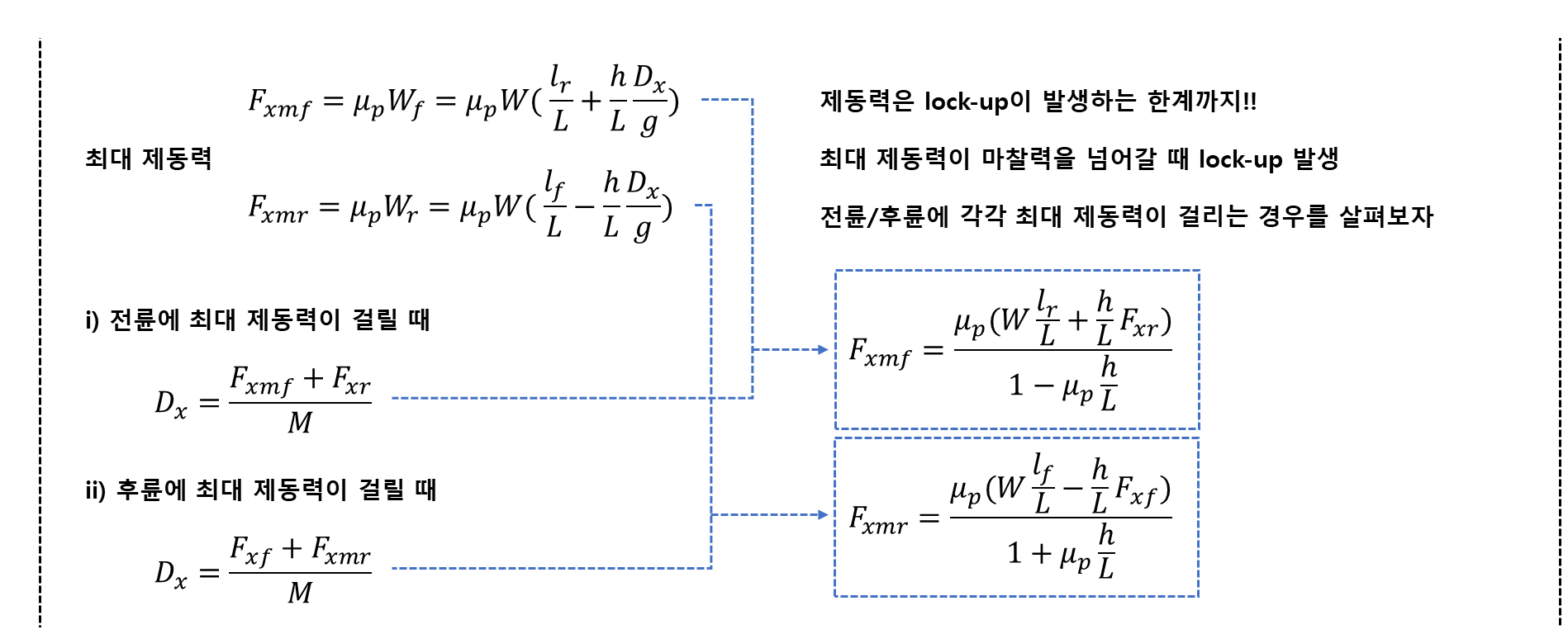
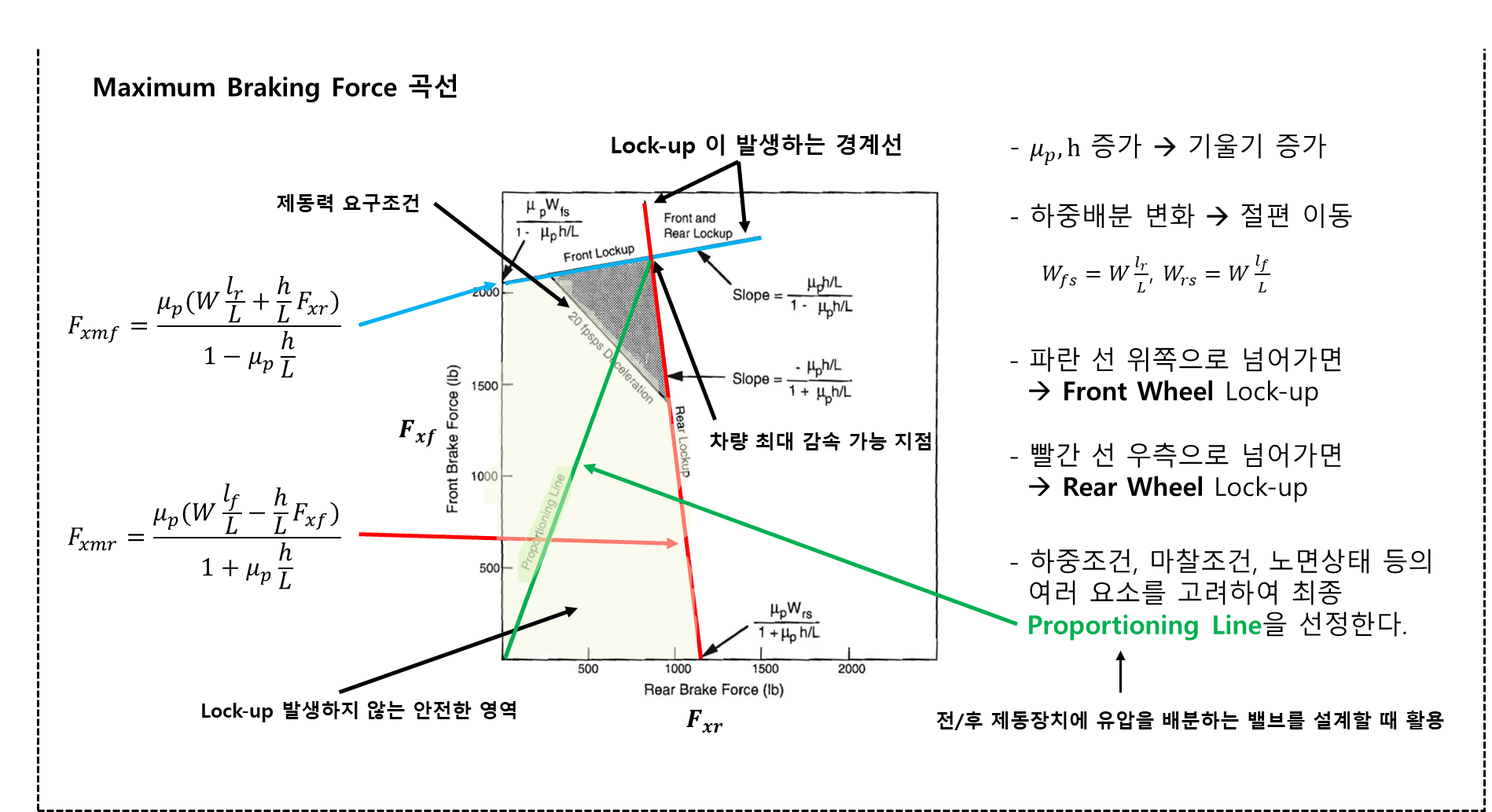
4. Driving Resistance
-
주행 저항 파트에서는 수학적 수식을 정리하지 않겠다. (시간이 너무 ... 크흠)
-
추후 필요하면 공부 할 수 있도록!
1) 구름저항 (Rolloing resistance)
-
자동차가 수평 노면 위를 굴러갈 때 받는 저항
-
타이어를 변형시키는 저항
-
노면을 변형시키는 저항
-
F_n (수직력), e (pneumatic trail)이 클수록, r_dyn (타이어 동하중 반지름) 이 작을수록 구름저항은 커진다.
-
공기압이 너무 적으면 타이어 동하중 반지름이 작겠지? => 구름저항 크겠지?
-
2) 공기저항 (Aero resistance)
-
주행 저항의 주요 요소
-
공기역학은 항력, 양력, 모멘트(roll, pitch, yaw), 소음에 영향을 미친다.
-
공기역학은 너무 어렵다.
3) 그 밖에...
-
기울기저항 (경사면에서 타이어 마찰력으로 인해 결정)
-
가속저항 (가속시 회전하는 부분의 질량으로 인해 발생하는 손실)
-
견인저항 (트레일러?)
등등 있는데 공기저항이 가장 크리티컬한 부분인 것 같다.
[2] Lateral Vehicle model
1. Kinematic Bicycle Model (저속선회 시)
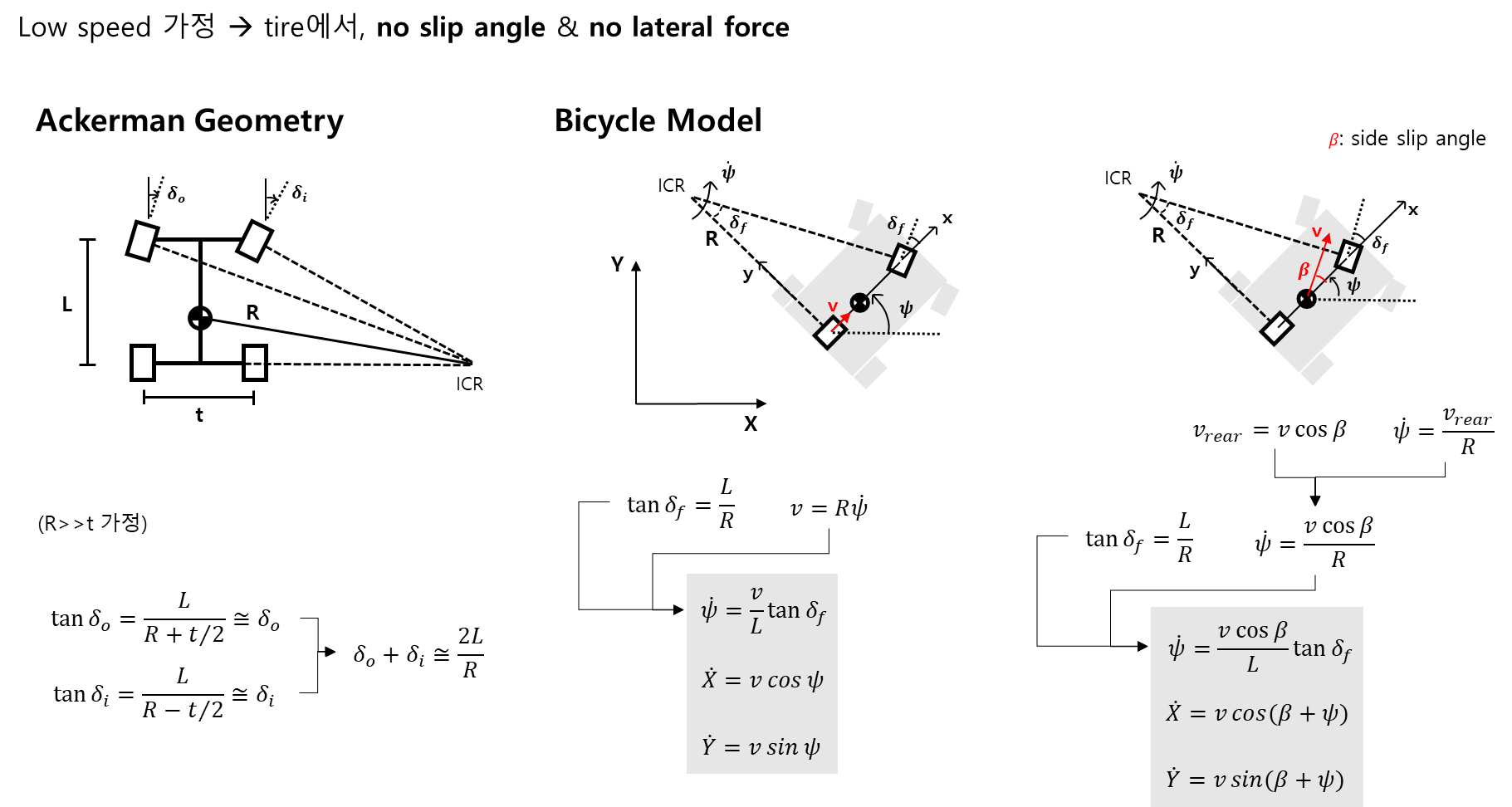
-
여기서 configuration (X_dot, Y_dot, psi_dot)은 관성 좌표계이다.
-
Kinematic Model은 단순 기하학적 형상을 기반으로 한 모델이기 때문에 간단하다.
하지만 요구사항이 높은 제어를 하기에는 정확성과 신뢰도가 높지 않다는 한계가 있다.
2. Before getting into Dynamic Model
- Kinematic Model과 달리 복잡하지만 정확하고 요구사항이 높은 제어가 가능한 차량의 Dynamic Model을 이해하기 위해 미리 짚고 넘어가야 할 개념들이 있다.
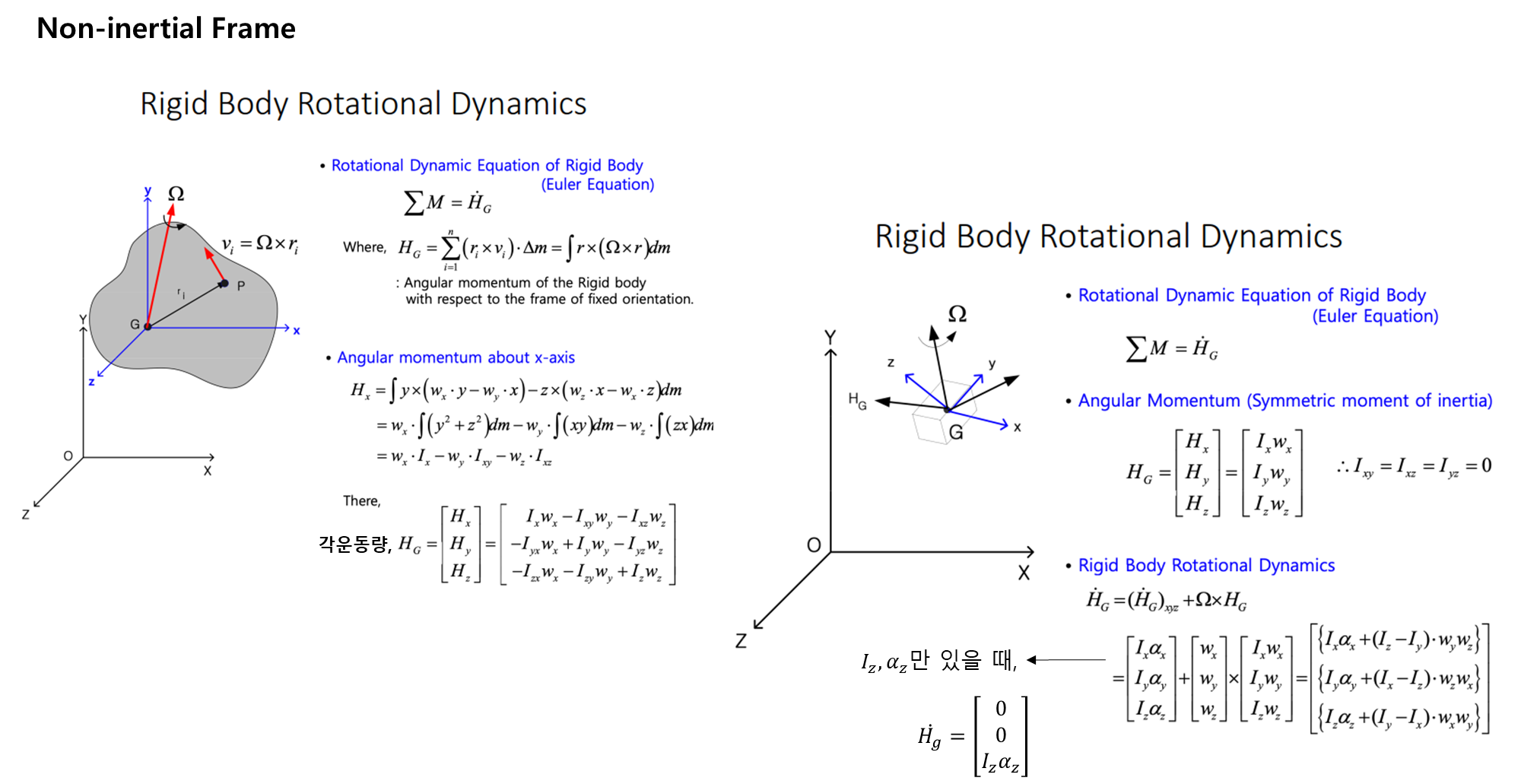
1) 비관성 좌표계
-
질점의 운동
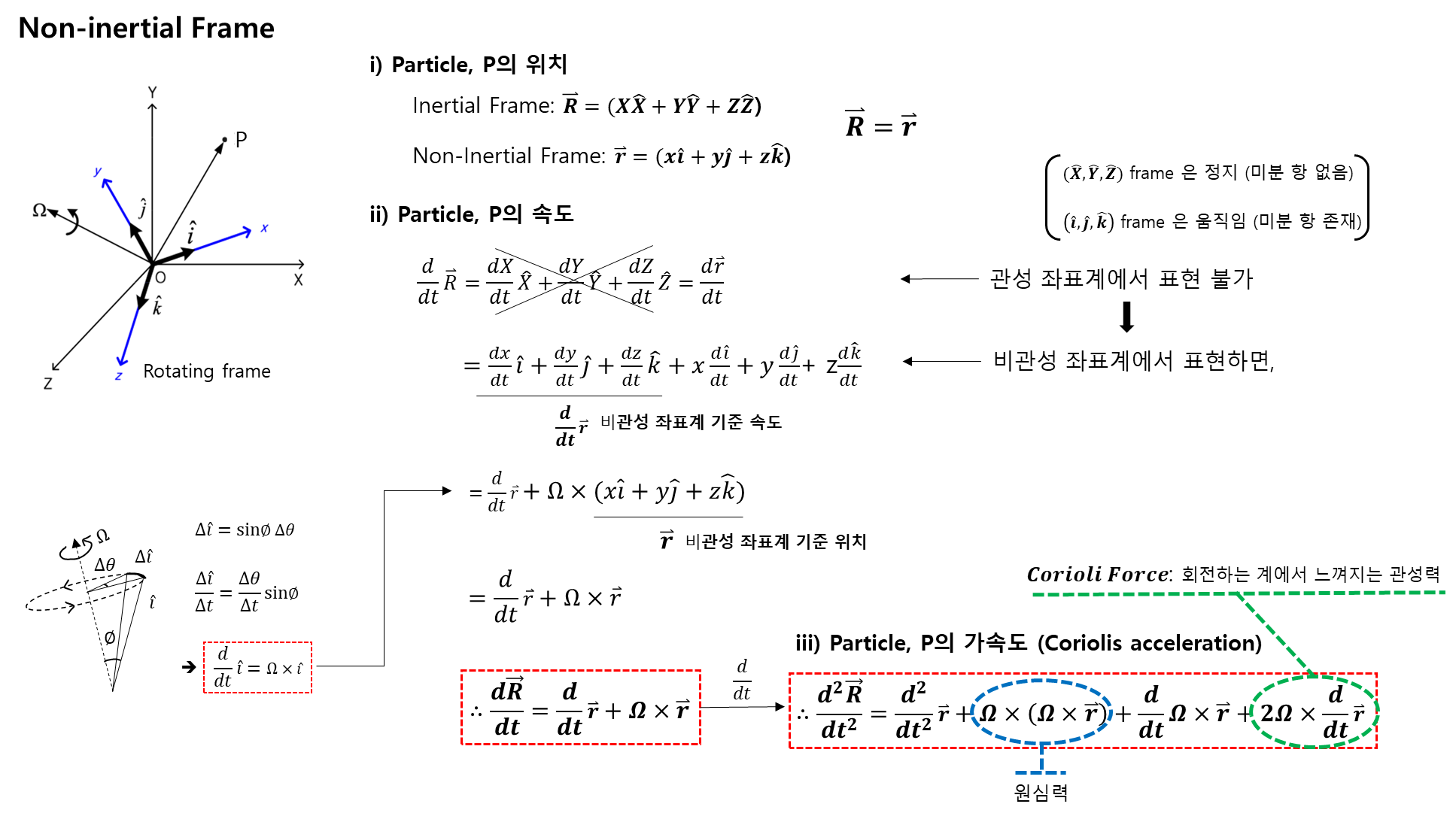
- 관성 좌표계의 속도 및 가속도는 비관성 좌표계의 속도와 위치로 표현된다.
-
강체의 운동

2) Clothoid & 3th-order Polynomial
-
Clothoid: 도로의 완화곡선으로 가장 많이 사용되는 모델로서 곡선의 길이에 따라 곡률이 변하는 곡선이다.
-
곡률과 곡선 길이가 비례하다. 즉, 회전 반경과 곡선 길이는 반비례하다.
(RL=C) -
아래 파란색 직선 영역에서 초록색 곡선 영역으로 넘어가는 중간에 위치한 빨간 선이 Clothoid 라고 한다.
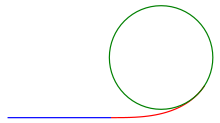
-
곡선을 부드럽게 이어주기 위해 사용된다고 한다.
-
매개변수를 이용한 표현 식이 있는데 필요하면 찾아보자~
-
-
클로소이드라는 차선 모델을 사용하는 건 알겠는데, 클로소이드는 최소 3차식으로 전개된다.
=> 센서로 부터 들어온 데이터로 최적의 차선을 3차 곡선으로 표현할 수 있을까?
=> 최소제곱(Least Square)법을 활용하여 데이터를 fitting한다. -
클로소이드 곡선을 y=C3x^3 + C2x^2 + C1x + C0 의 3차식으로 두었을 때,
- 1번 미분 dy/dx = theta (Heading of Path) / 2nd-order
- 2번 미분 d^2y/(dx)^2 = kappa = 1/R (Curverture of Path) / 1st-order
- 3번 미분 d^3y/(dx)^3 (Cureverture Derivative) / Constant
3) Fitting


4) Tire Force
-
저속구간이 아닌 실제 주행 시 타이어에 slip이 발생한다.
-
Tire-Slip으로 인해 차량의 body frame 기준 y축으로의 Lateral Force가 발생하고, 이들은 서로 비례한다.
-
F_y = C_alpha x alpha
-
F_y와 slip angle은 Cornering Stiffness라는 비례상수를 취한다.
-
이 둘의 관계를 나타내는 그래프는 실험적으로 얻어진다.
-
-
Magic Formula Tire Model
-
Lateral Force와 Cornering Stiffness의 비례관계를 나타낸 그래프이다.
-
추후 Lateral Dynamic Model을 유도하는데 사용된다.
-
여기까지 차량의 Dynamic Model을 이해하기 위한 사전 지식을 짧게 알아보았다.
3. State Equation of 2 DOF Bicycle Model
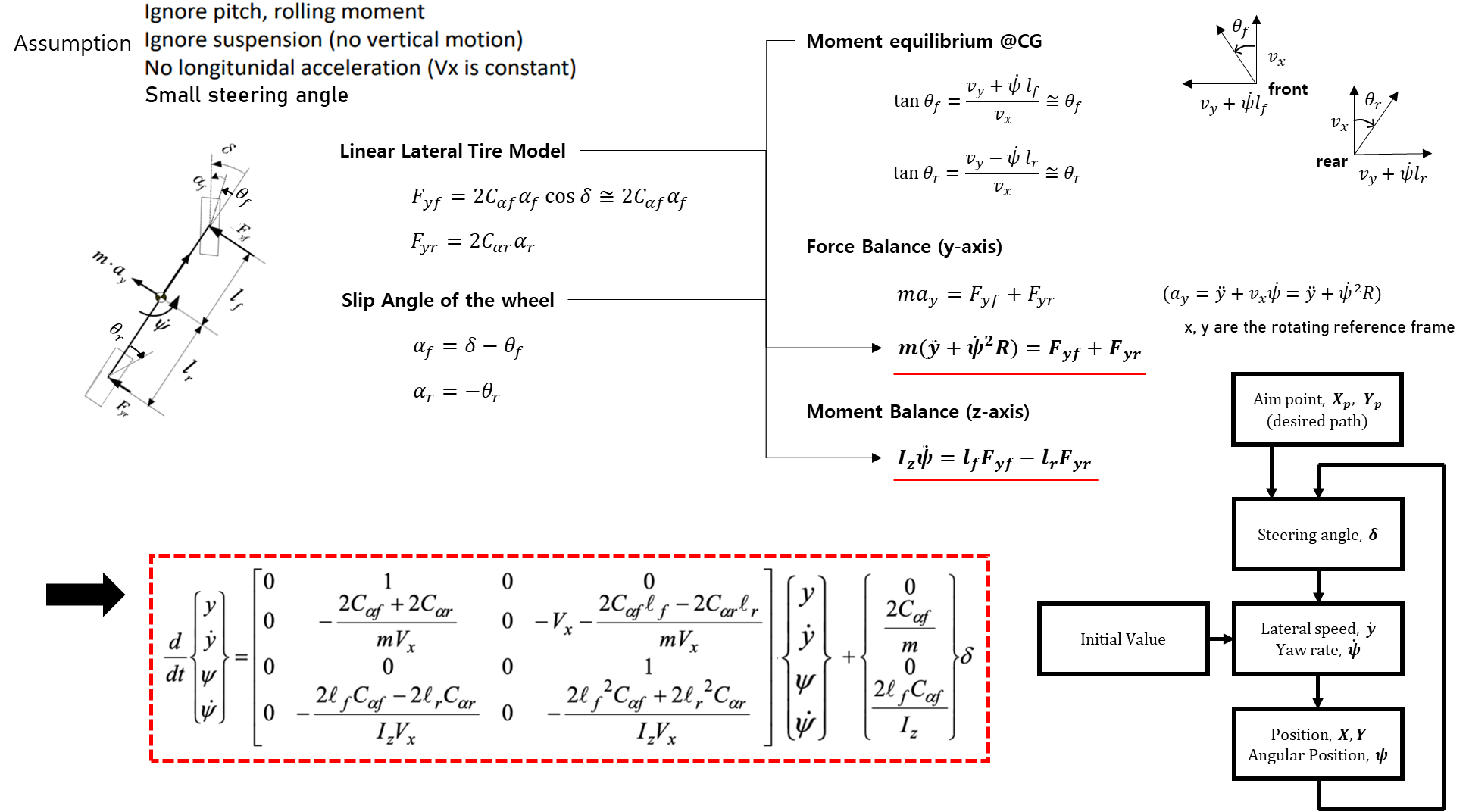
[3] Vehicle Control
1. Longitudinal Control
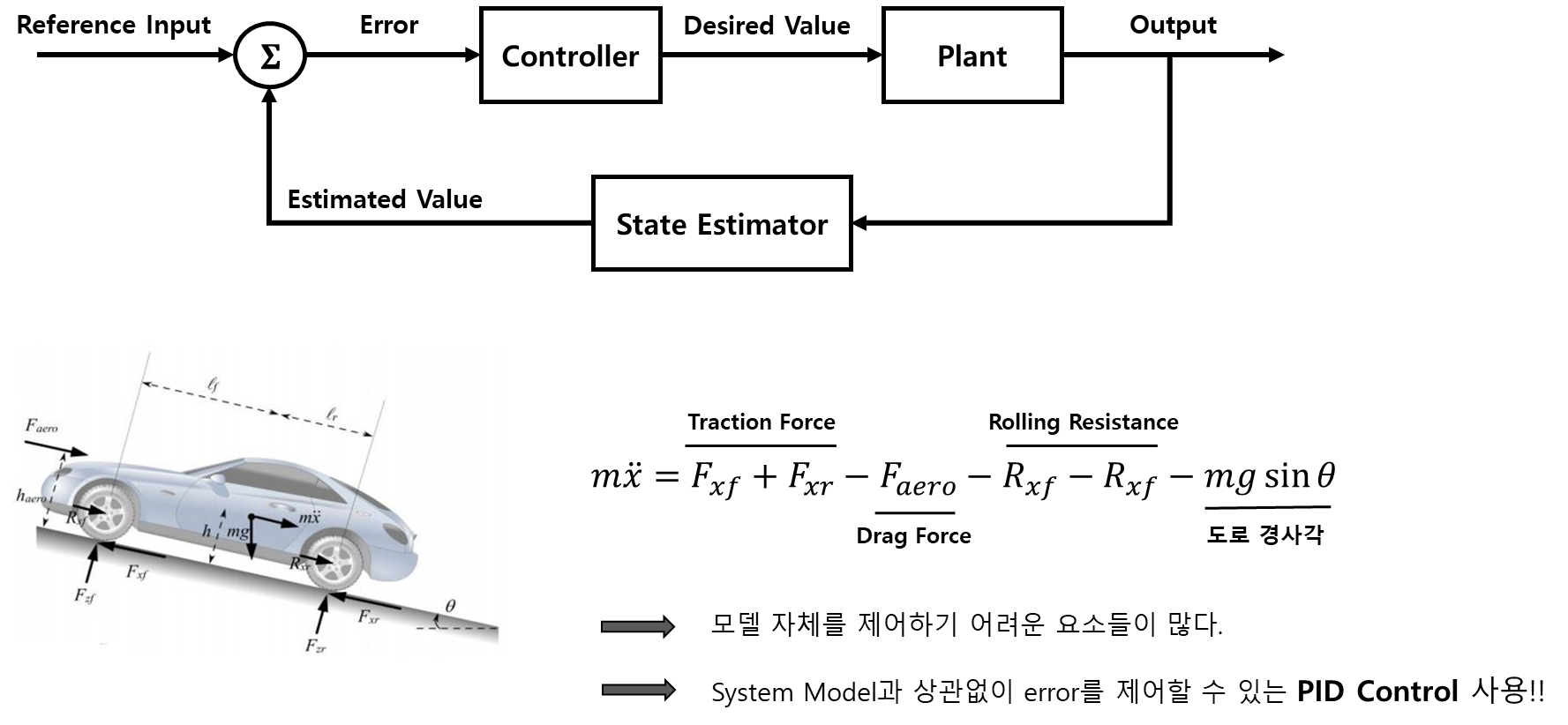

- speed control과 spaceing control을 결정하는 maneuver planning 시스템을 설계하는게 어렵다고 한다.
2. Lateral Control
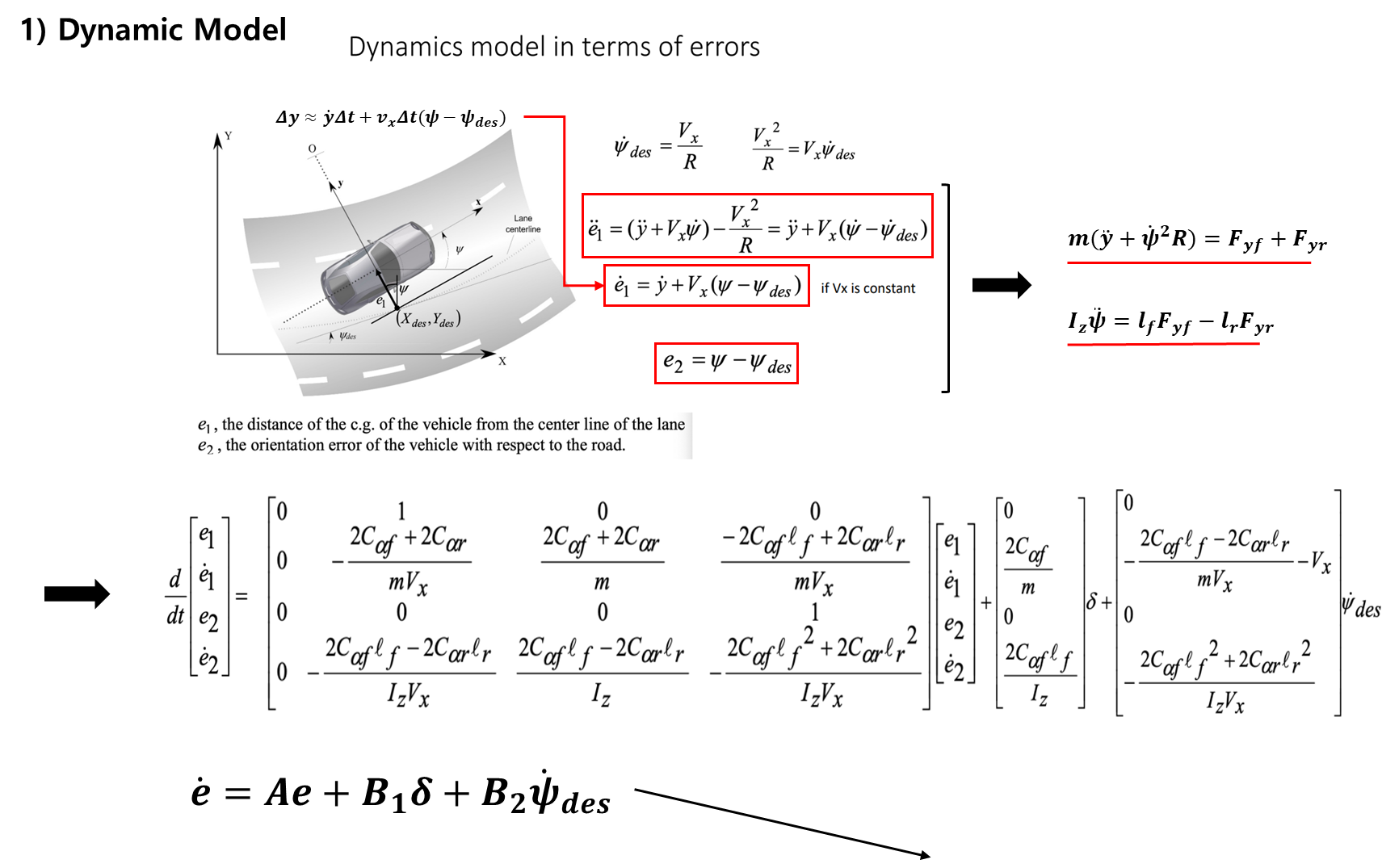
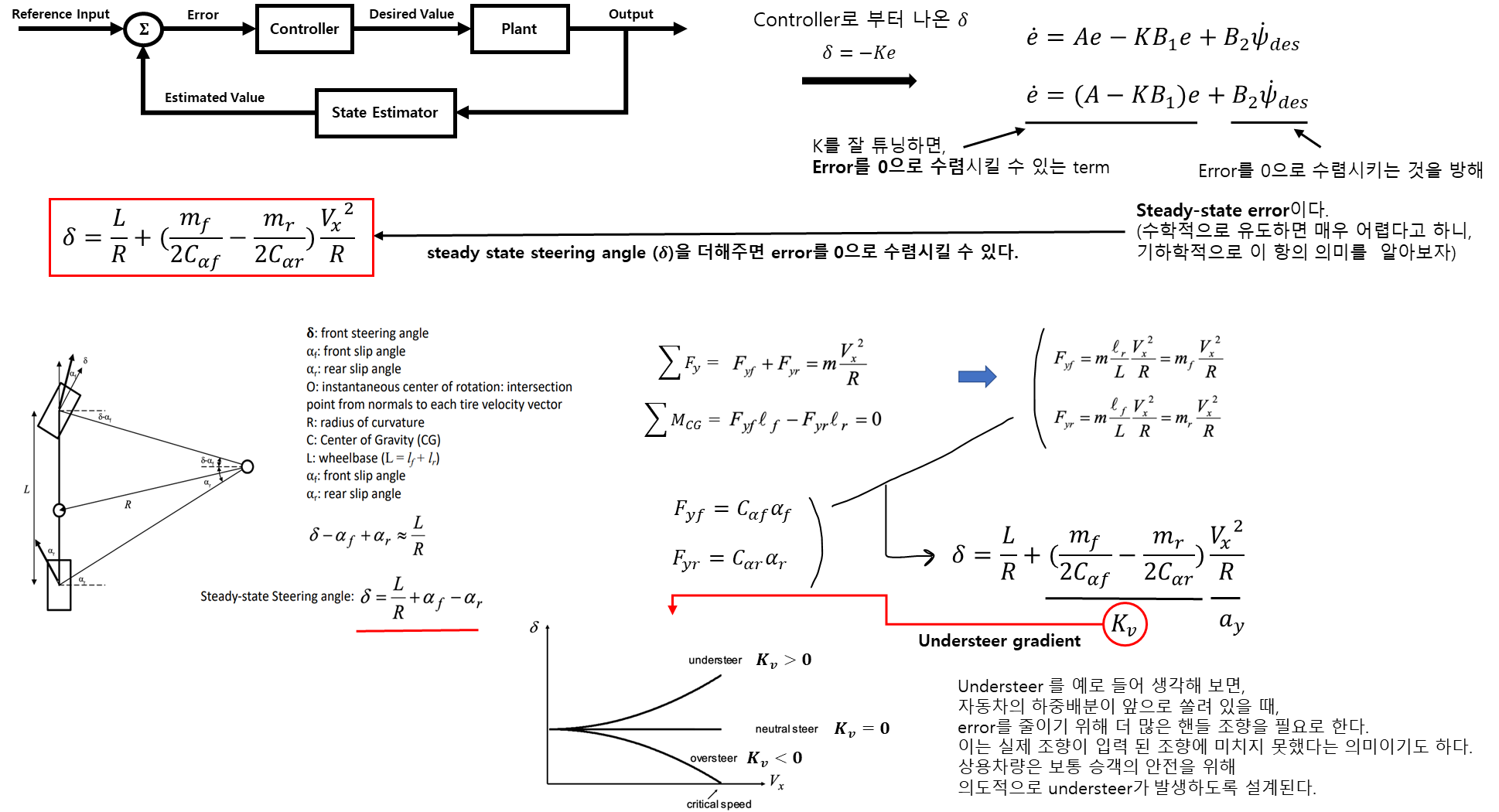
- Dynamics Model in terms of Errors
<출처>
(1) Programmers K-Digital-Training: 자율주행 데브코스 Planning & Control, 고전제어
(2) Thomas D. Gillespie, Fundamentals of Vehicle Dynamics

