[PLONK 1.] PLONK-style Arithmetization

이번 시리즈는 zk-SNARK를 발전시킨 개념인 PLONK에 대해 알아보도록 하겠습니다. PLONK-style arithmetization과 polynomial commitment의 종류 중 하나인 KZG commitment, 그리고 Plookup에 대해서도 다룰 예정입니다.

이번 글에서는 PLONK-style arithmetization에 대해서 알아보겠습니다. 이 글은 Vitalik Buterin의 Understanding PLONK 를 기반으로 작성됐습니다.

Why PLONK?

PLONK-style arithmetization을 설명하기에 앞서, PLONK라는 개념이 왜 나왔는지에 대해 (개인적인 해석이 담긴) 설명하겠습니다.

앞서, zk-SNARK에서는 증명하고자 하는 computational problem을 arithmetic circuit으로 표현한 후, R1CS를 circuit에서 추출했습니다. 그리고 R1CS를 compact하게 표현하기 위해 QAP라는 형태로 변환시켰습니다. 이후, Verifiable Blind Evaluation 을 이용해 Prover는 Verifier에게 QAP를 만족하는 다항식을 알고 있음을 증명할 수 있었습니다. 그리고 증명 과정이 non-interactive하게 작동할 수 있도록 trusted setup 과정이 도입됐습니다.

기존의 SNARK에서 R1CS를 이용해 arithmetic circuit의 constraint를 표현했는데, R1CS의 벡터의 크기가 circuit에 존재하는 모든 변수의 개수와 같아야 했습니다. R1CS의 solution vector가 circuit을 consistent하게 만들어야 하기 때문입니다. 이는 circuit의 크기가 커질수록 R1CS 벡터들도 비대해진다는 문제가 있습니다. 이를 해결하기 위해 PLONK에서는 gate 간의 wire의 값들을 consistent하게 만들어 주는 constraint를 분리합니다.(개인적인 해석이니, 잘못 이해한 것이라면 댓글로 코멘트 남겨주세요!) 따라서 arithmetic circuit을 QAP가 아닌 새로운 형태로 변환하게 되는데, 이를 PLONK-style arithmetization이라고 합니다.

그리고 기존의 SNARK에서는 QAP 별로 별도의 trusted setup 과정이 필요하다는 단점이 존재했습니다. PLONK에서는 universal하고 updateable한 trusted setup을 도입하기 위해 polynomial commitment라는 새로운 scheme을 사용합니다. Polynomial commitment는 이후 글에서 다루도록 하겠습니다.

PLONK-style arithmetization

이제 PLONK에서는 어떻게 arithmetic circuit을 변환하는지 살펴보겠습니다. Prover가 x^3 + x + 5 = 35를 만족하는 x 값을 알고 있음을 증명하려 합니다. 이 문제는 다음과 같은 arithmetic circuit으로 표현될 수 있습니다.

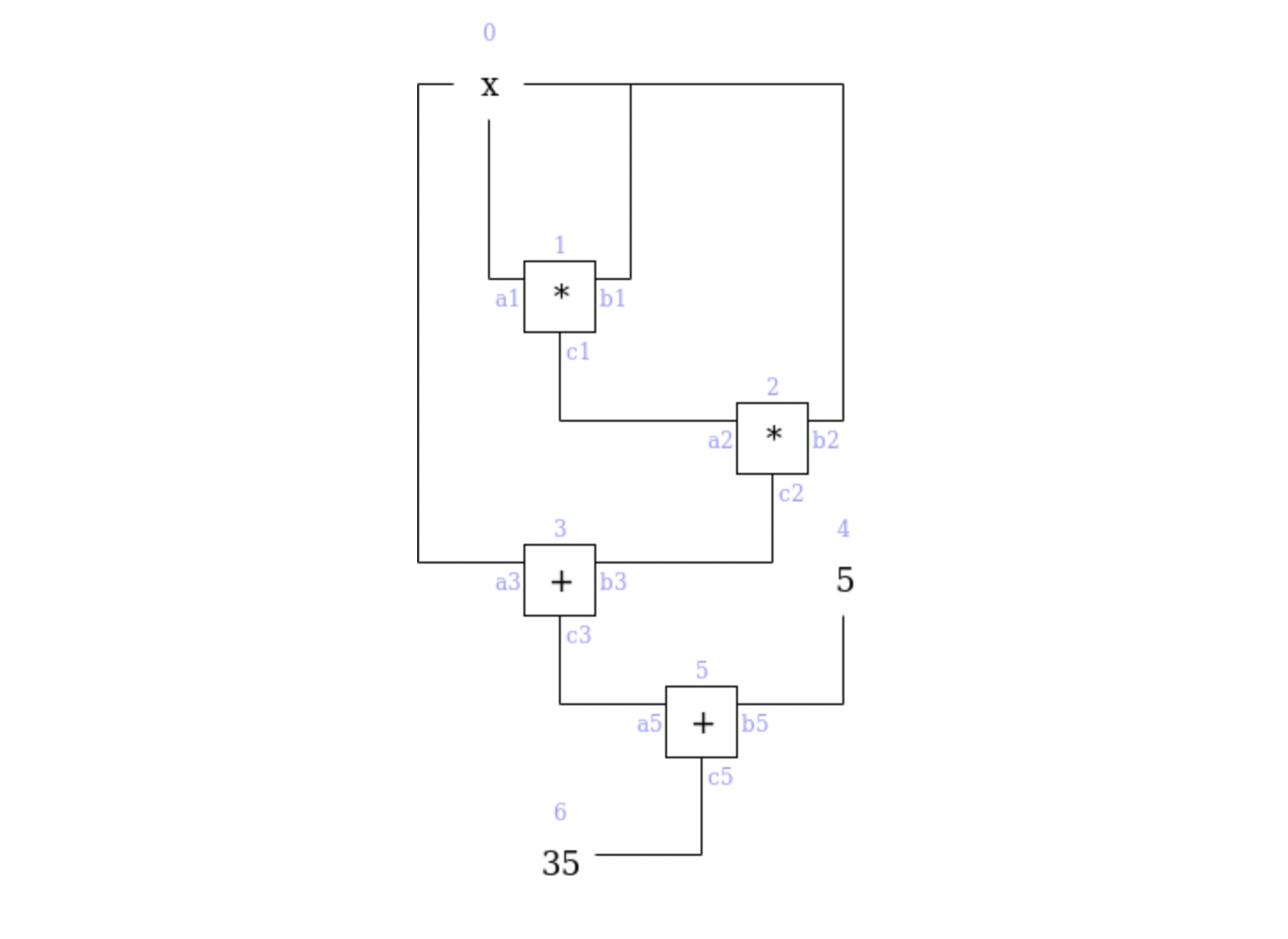
Prover는 위 arithmetic circuit을 만족하는 wire의 값들을 알고 있음을 증명해야 하는데, 이를 가리켜 witness라고 명명합니다.

PLONK에는 Prover의 witness가 arithmetic circuit을 만족하는지 검사하기 위해 두 가지 constraint이 존재합니다. 각 gate에서 wire의 값들이 만족해야 하는 gate constraint와, circuit이 consistent해지도록 wire들 간에 성립해야 하는 copy constraint가 있습니다.

Gate constraint

먼저 gate constraint를 알아보겠습니다. $i$번째 gate의 left, right, output wire들을 각각 $a_i, b_i, c_i$라고 할 때 gate constraint는 다음과 표현됩니다.

위 식에서 $Q_{L_i}, Q_{R_i}, Q_{O_i}, Q_{M_i}, Q_{C_i}$는 gate의 종류에 따라 결정됩니다.

Multiplication gate에서는 $a_i * b_i = c_i$를 만족하므로 $Q_{L_i} = 0, Q_{R_i} = 0, Q_{O_i} = 1, Q_{M_i} = -1, Q_{C_i} = 0$이 됩니다.

Addition gate에서는 $a_i + b_i = c_i$를 만족하므로 $Q_{L_i} = 1, Q_{R_i} = 1, Q_{O_i} = -1, Q_{M_i} = 0, Q_{C_i} = 0$이 됩니다.

Constant gate에서는 $c_i = C$를 만족하므로 $Q_{L_i} = 0, Q_{R_i} = 0, Q_{O_i} = -1, Q_{M_i} = 0, Q_{C_i} = C$가 됩니다.

총 n개의 gate가 있다고 하면, n개의 gate constraint가 존재합니다.

위 n개의 식을 하나의 식으로 compact하기 위해 다음과 같은 다항식들을 정의합니다. 각 gate들이 $0, \dots, n - 1$에 대응된다고 할 때, 각각 $[(i, Q_{L_i})]_{i=1}^n$ $[(i, Q_{R_i})]_{i=1}^n$ $[(i, Q_{O_i})]_{i=1}^n$ $[(i, Q_{M_i})]_{i=1}^n$ $[(i, Q_{C_i})]_{i=1}^n$을 interpolate하는 $(n - 1)$차 다항식을 $Q_L(x), Q_R(x), Q_O(x), Q_M(x), Q_C(x)$라고 정의하겠습니다.

그리고 각각 $[(i, a_i)]_{i=1}^n$ $[(i, b_i)]_{i=1}^n$ $[(i, c_i)]_{i=1}^n$을 interpolate하는 $(n - 1)$차 다항식들을 각각 $a(x), b(x), c(x)$로 정의하겠습니다.

위 등식은 $x = 0, \dots , n - 1$일 때 성립하므로 어떤 다항식 $H(x)$가 존재해 다음이 성립함을 알 수 있습니다.

Prover는 위 조건을 만족하는 다항식 $a(x), b(x), c(x)$를 알고 있음을 증명해야 합니다.

Copy constraint

앞서 살펴본 gate constraint에서는 예를 들어 '$i$번째 gate의 output wire 값이 $(i + 1)$번째 gate의 left input wire 값과 같아야 한다'는 조건은 표현되지 않았습니다. Circuit이 consistent해지기 위해서는 $c(1) = b(2), \;c(2) = a(4)$와 같은 조건들을 만족해야 하는데, 이를 가리켜 copy constraint라고 합니다. PLONK에서는 permutation check를 통해 Prover의 witness가 copy constraint를 만족하는지 검사할 수 있습니다.

Multiset equality check

Permutation check에 대해서 알아보기에 앞서, multiset equality check에 대해서 소개하겠습니다. Multiset equality check를 통해 벡터 $a = (a_1, \dots, a_n)$의 원소들과 $b = (b_1, \dots, b_n)$의 원소들을 같은 원소들끼리 대응시켰을 때 일대일 대응 관계가 성립하는지 확인할 수 있습니다. 예를 들어 $(1, 1, 3, 4)$와 $(1, 3, 4, 1)$은 multiset-equal하지만, $(1, 2, 3, 4)$와는 multiset-equal하지 않습니다.

벡터 $a, b$의 원소들이 field $\mathbb{F}$에 존재할 때, $\gamma \in \mathbb{F}$인 random한 원소 $\gamma$을 선택해 다음이 성립하는지 확인합니다:

Field $\mathbb{F}$의 크기가 매우 클 때, 위 등식이 성립한다면 Schwartz-Zippel Lemma에 의해 $(a_1, \dots, a_n)$과 $(b_1, \dots, b_n)$이 매우 높은 확률로 multiset-equal함을 알 수 있습니다.

Permutation check

벡터 $a = (a_1, \dots, a_n)$과 $b = (b_1, \dots, b_n)$이 있고, permutation $\sigma : [n] \rightarrow [n]$이 존재할 때, $i \in [n], \;b_i = a_{\sigma(i)}$을 만족하는지 확인하기 위해 permutation check를 사용합니다.

$b = \sigma(a)$를 만족한다는 것은, $((a_1, 1), \dots, (a_n, n))$과 $((b_1, \sigma(1)), \dots, (b_n, \sigma(n)))$이 multiset-equal이 되는 것과 필요충분조건임을 알 수 있습니다. 앞서 살펴본 multiset equality check는 단일 원소들로 이루어진 벡터에 대해서 살펴보았기 때문에, random한 값 $\beta \in \mathbb{F}$를 준비해, $((a_1, 1), \dots, (a_n, n))$과 $((b_1, \sigma(1)), \dots, (b_n, \sigma(n)))$의 각 원소들을 다음과 같이 변환합니다.

이제 $(a_1', \dots, a_n')$과 $(b_1', \dots, b_n')$ 간에 multiset equality check를 합니다.

Copy constraint

이제 permutation check를 이용해 PLONK의 copy constraint를 나타내는 방법을 살펴보겠습니다.

Arithmetic circuit의 $i$번째 gate의 left input, right input, output의 값을 각각 $a_i, b_i, c_i$라고 명명하면, 다음과 같이 총 $3n$개의 witness 값이 존재합니다.

2번째 gate의 output wire 값이 $n$번째 gate의 left input wire 값과 동일하면, $a_n = c_2$가 성립함을 알 수 있습니다. 그럼 다음과 같이 $a_n$과 $c_2$의 자리를 바꿔 보겠습니다.

$i \in [n]$에 대해 $a_i$를 $i$, $b_i$를 $n + i$, 그리고 $c_i$를 $2n + i$에 대응된다고 하겠습니다. $\sigma(n) = 2n + 2, \; \sigma(2n + 2) = n$를 만족하는 permutation $\sigma : [3n] \rightarrow [3n]$가 존재하고, 위의 witness를 $f$, 아래의 witness를 $g$라고 할 때 $g = \sigma(f)$를 만족함을 알 수 있습니다. 이는 Permutation check를 통해 다음과 같은 등식으로 표현할 수 있습니다.

마치며

이번 글에서는 PLONK arithmetization에 사용되는 math building block들에 대해서 알아보았습니다. 다음 글에서 KZG commitment에 대해 다루고 난 후, 실제 PLONK에서 Prover가 다항식을 증명하기 위한 protocol에 대해 알아보겠습니다.