[백준] 10844번: 쉬운 계단 수 (Python)

문제

45656이란 수를 보자.
이 수는 인접한 모든 자리의 차이가 1이다. 이런 수를 계단 수라고 한다.
N이 주어질 때, 길이가 N인 계단 수가 총 몇 개 있는지 구해보자. 0으로 시작하는 수는 계단수가 아니다.

입력

첫째 줄에 N이 주어진다. N은 1보다 크거나 같고, 100보다 작거나 같은 자연수이다.

출력

첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.

풀이

길이가 N일 때 앞, 뒤로 차이가 1이 나는 숫자가 몇 개인지를 구하는 문제이다.
뒤에 있는 숫자를 기준으로, 앞에 올 수 있는 숫자의 경우의 수를 구한다.
자릿수마다 각각의 숫자 앞에 올 수 있는 경우의 수가 다르므로 2차원 DP 테이블을 만든다.

DP[N의 수][N 자리 숫자일 때, 해당 숫자 앞에 올 수 있는 일의 자리 수]

0 앞에 올 수 있는 숫자는 1밖에 없고,
9 앞에 올 수 있는 숫자는 8밖에 없지만
그 외에 2~8까지는 ±1한 숫자 2개가 올 수 있다.

따라서 점화식을 작성하면

j가 0일 때, dp[i][j] = dp[i-1][j+1]
j가 9일 때, dp[i][j] = dp[i-1][j-1]
j가 2~8일 때, dp[i][j] = dp[i-1][j-1] + dp[i-1][j+1]

이다.

이 때, 유의할 점은 1자리 수일 때 초깃값은 1이지만 0으로는 시작할 수 없다고 했으므로,
dp[1][0]은 0으로 초기화시켜주어야 한다.

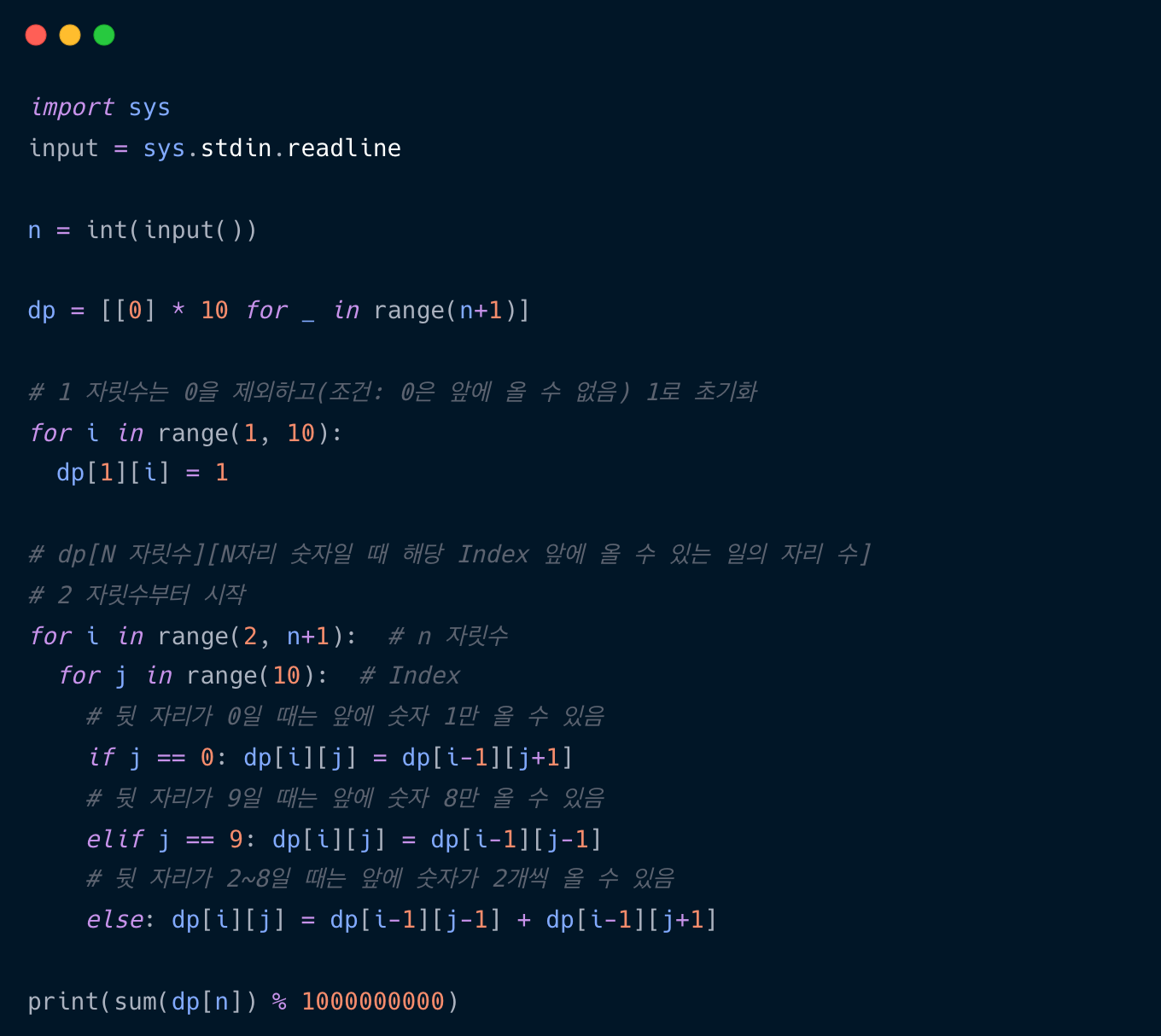
Python 코드