문제
지원이에게 2진 수열을 가르쳐 주기 위해, 지원이 아버지는 그에게 타일들을 선물해주셨다. 그리고 이 각각의 타일들은 0 또는 1이 쓰여 있는 낱장의 타일들이다.
어느 날 짓궂은 동주가 지원이의 공부를 방해하기 위해 0이 쓰여진 낱장의 타일들을 붙여서 한 쌍으로 이루어진 00 타일들을 만들었다. 결국 현재 1 하나만으로 이루어진 타일 또는 0타일을 두 개 붙인 한 쌍의 00타일들만이 남게 되었다. 그러므로 타일로 더 이상 크기가 N인 모든 2진 수열을 만들 수 없게 되었다.
예를 들어 N=1 일 때 1만 만들 수 있고, N=2일 때는 00, 11을 만들 수 있다. (01, 10은 만들 수 없게 되었다.)
또한 N=4일 때는 0011, 1100, 1111 등 총 5개의 2진 수열을 만들 수 있다.
우리의 목표는 N이 주어졌을 때 만들 수 있는 모든 가짓수를 세는 것이다. 단 타일들은 무한히 많은 것으로 가정하자.
입력
첫 번째 줄에 자연수 N이 주어진다. (1 ≤ N ≤ 1,000,000)
출력
첫 번째 줄에 지원이가 만들 수 있는 길이가 N인 모든 2진 수열의 개수를 15746으로 나눈 나머지를 출력한다.
풀이 과정
이 문제에는 다음과 같은 규칙이 존재한다.
DP[1] = 1(1)
DP[2] = 2(11, 00)
DP[3] = 3(111, 100, 001)
DP[4] = 5(1111, 1100, 1001, 1100, 0000)
위 결과를 보면 알 수 있듯이 DP[n]은 DP[n-1]+DP[n-2]의 형식으로 쌓아가는 것을 볼 수 있다.
1은 단독으로 쓰일 수 있지만 0은 단독으로 쓰일 수 없기 때문에
현재 결과에 '1'만을 붙여 다음 값을 만들 수 있지만
'0'만을 붙여 다음 값을 만들 수 없으므로 '00'을 붙여 다음 값을 만들게 된다.
하지만 '00'은 길이가 2이므로 현재 값에 붙이면 길이가 초과하게 되므로 이전 값에 붙여주어야 한다.
예를 들어,
DP[4]의 경우에는
DP[3]의 각각의 값에 1을 붙인 것과
DP[2]의 각각의 값에 00을 붙인 것과 같다.
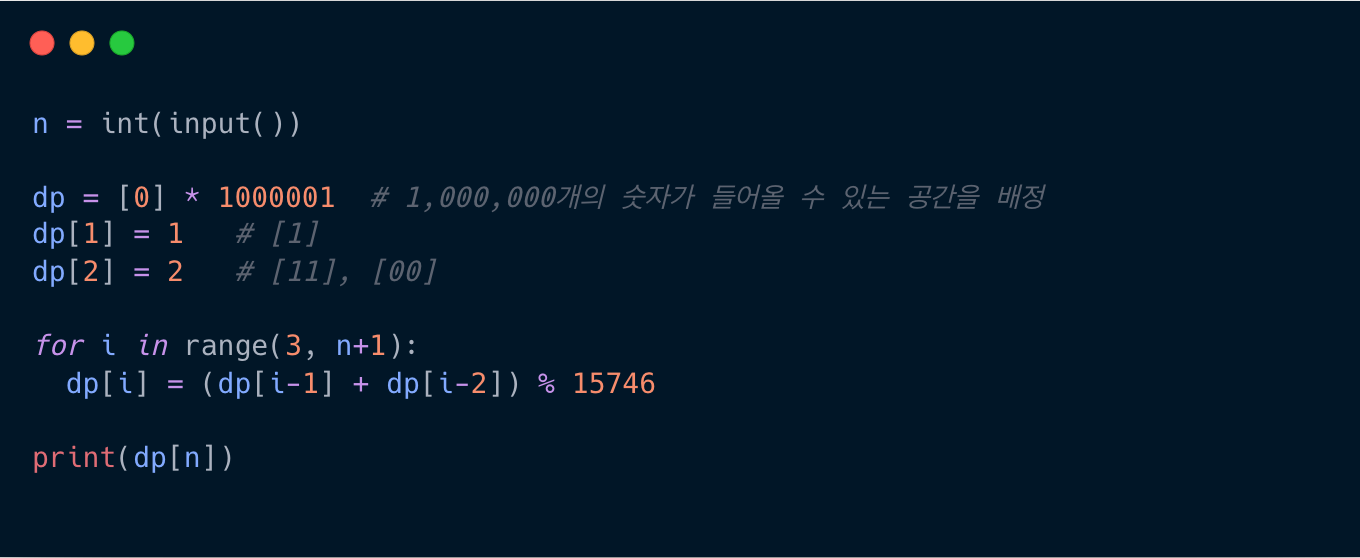
이 특징을 살려 코드를 구현하면 다음과 같다.
다만, 문제의 n이 최대 1,000,000이므로 계산 중간에 int의 범위를 벗어나는 경우가 생기므로
맨 마지막 결과가 아닌 중간중간에 %15746을 해야 한다.
Python 코드