[프로그래머스] 교점에 별 만들기

🗃️문제 설명

👉단순 구현

Ax + By + C = 0으로 표현할 수 있는 n개의 직선이 주어질 때, 이 직선의 교점 중 정수 좌표에 별을 그리려 합니다.

예를 들어, 다음과 같은 직선 5개를

• 2x - y + 4 = 0
• -2x - y + 4 = 0
• -y + 1 = 0
• 5x - 8y - 12 = 0
• 5x + 8y + 12 = 0

좌표 평면 위에 그리면 아래 그림과 같습니다.

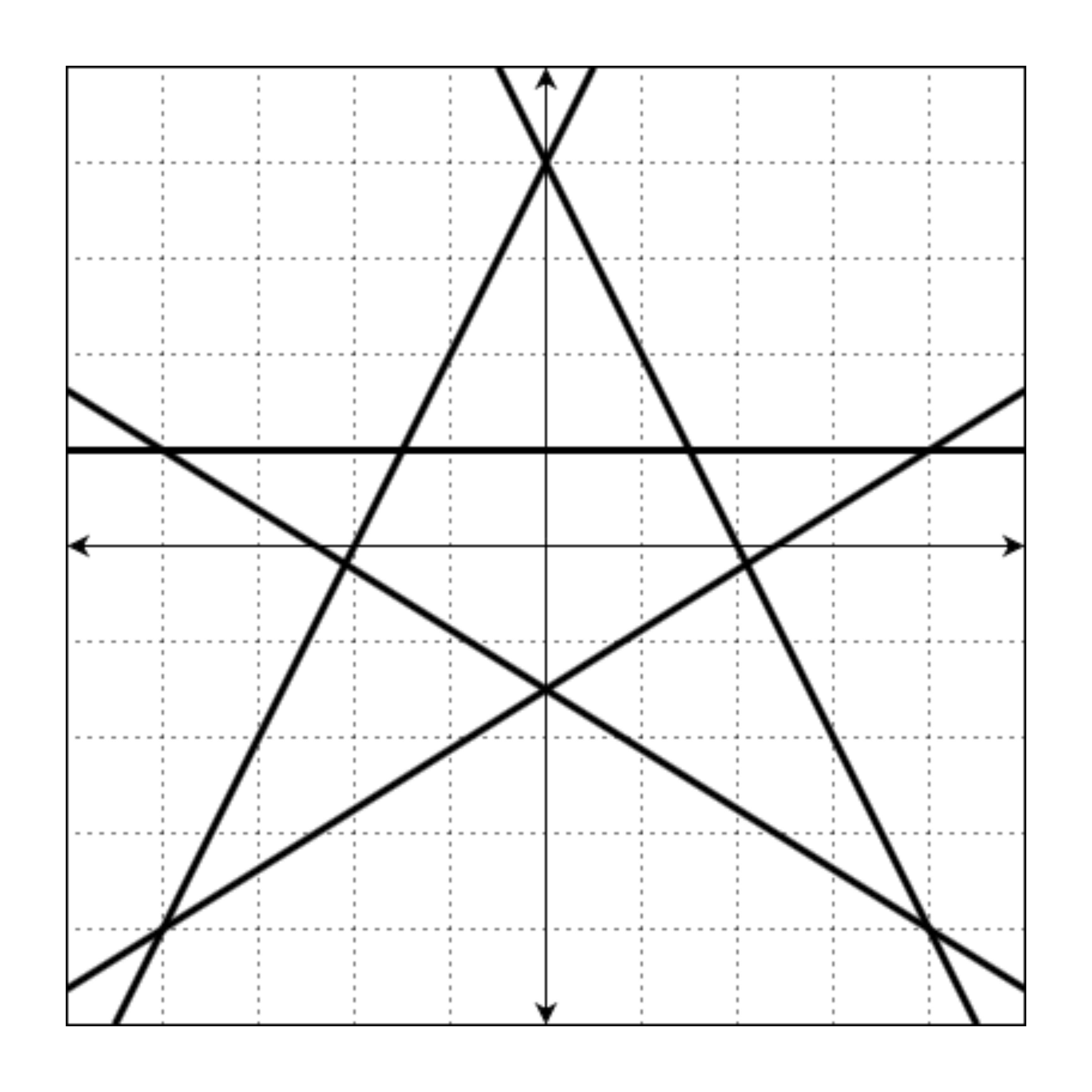
이때, 모든 교점의 좌표는 (4, 1), (4, -4), (-4, -4), (-4, 1), (0, 4), (1.5, 1.0), (2.1, -0.19), (0, -1.5), (-2.1, -0.19), (-1.5, 1.0)입니다. 이 중 정수로만 표현되는 좌표는 (4, 1), (4, -4), (-4, -4), (-4, 1), (0, 4)입니다.

만약 정수로 표현되는 교점에 별을 그리면 다음과 같습니다.

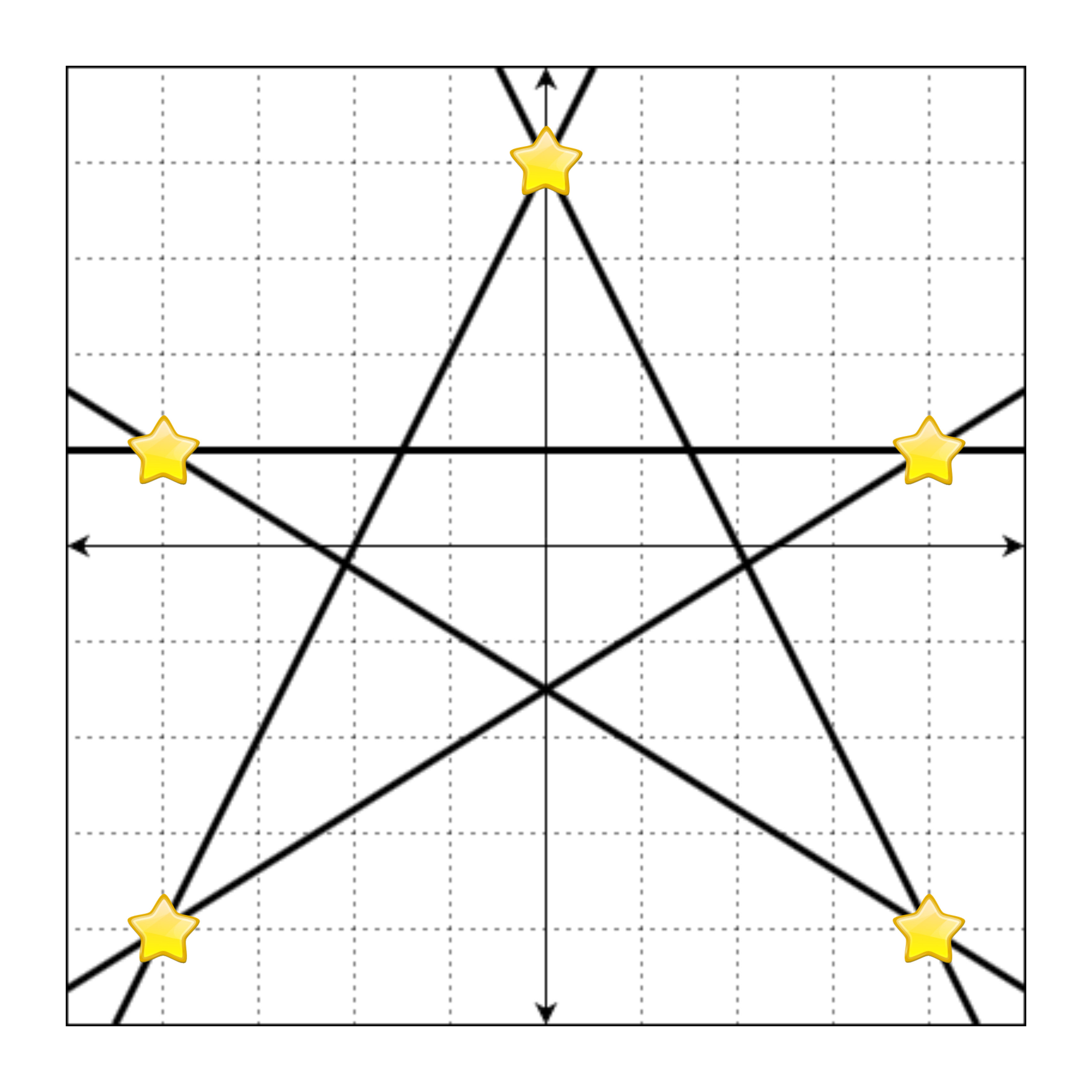
위의 그림을 문자열로 나타낼 때, 별이 그려진 부분은 *, 빈 공간(격자선이 교차하는 지점)은 .으로 표현하면 다음과 같습니다.

"..........."  
".....*....."  
"..........."  
"..........."  
".*.......*."  
"..........."  
"..........."  
"..........."  
"..........."  
".*.......*."  
"..........."  

이때 격자판은 무한히 넓으니 모든 별을 포함하는 최소한의 크기만 나타내면 됩니다.

따라서 정답은

"....*...."  
"........."  
"........."  
"*.......*"  
"........."  
"........."  
"........."  
"........."  
"*.......*"  

입니다.

직선 A, B, C에 대한 정보가 담긴 배열 line이 매개변수로 주어집니다. 이때 모든 별을 포함하는 최소 사각형을 return 하도록 solution 함수를 완성해주세요.

🖥️코드

def solution(line):
    answer = []
    # 격자판 최대 영역 변수
    INF = int(1e15)
    MAX_X = -INF; MAX_Y = -INF
    MIN_X = INF; MIN_Y = INF
    dots = []

    for i in range(len(line)):
        a, b, c = line[i]
        for j in range(i + 1, len(line)):
            d, e, f = line[j]
            # 두 직선의 기울기가 같아 평행하다면 교점은 안 생김
            if a * e == b * d:
                continue
            # 두 직선의 교점 좌표(x, y)
            x = (c * e - b * f) / (b * d - a * e)
            y = (a * f - c * d) / (b * d - a * e)
            # 정수값만
            if int(x) == x and int(y) == y:
                MIN_X = min(MIN_X, int(x))
                MAX_X = max(MAX_X, int(x))
                MIN_Y = min(MIN_Y, int(y))
                MAX_Y = max(MAX_Y, int(y))               
                dots.append([int(x), int(y)])

    width = abs(MAX_X - MIN_X + 1)
    height = abs(MAX_Y - MIN_Y + 1)
    array = [["."] * width for _ in range(height)]  
    
    # 오래 걸린 부분 : 음수 좌표의 경우 약간의 변환이 필요
    for x, y in dots:
        if MIN_X < 0:
            nx = x + abs(MIN_X)
        else:
            nx = x - MIN_X
        
        if MIN_Y < 0:
            ny = y + abs(MIN_Y)
        else:
            ny = y - MIN_Y
        array[ny][nx] = "*"
    
    for i in array:
        answer.append("".join(i))
    return answer[::-1]

🔒문제 출처

프로그래머스 - 교점에 별 만들기