
🗃️문제 설명
그래프가 주어졌을 때, 그 그래프의 최소 스패닝 트리를 구하는 프로그램을 작성하시오.
최소 스패닝 트리는, 주어진 그래프의 모든 정점들을 연결하는 부분 그래프 중에서 그 가중치의 합이 최소인 트리를 말한다.
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이 가중치 C인 간선으로 연결되어 있다는 의미이다. C는 음수일 수도 있으며, 절댓값이 1,000,000을 넘지 않는다.
그래프의 정점은 1번부터 V번까지 번호가 매겨져 있고, 임의의 두 정점 사이에 경로가 있다. 최소 스패닝 트리의 가중치가 -2,147,483,648보다 크거나 같고, 2,147,483,647보다 작거나 같은 데이터만 입력으로 주어진다.
첫째 줄에 최소 스패닝 트리의 가중치를 출력한다.
🖥️코드
import sys
sys.setrecursionlimit(10**8)
input = sys.stdin.readline
def find(x):
if parent[x] != x:
parent[x] = find(parent[x])
return parent[x]
def union(a, b):
a = find(a)
b = find(b)
if a < b:
parent[b] = a
else:
parent[a] = b
V, E = map(int, input().split())
parent = [i for i in range(V+1)]
edges = []
for _ in range(E):
a, b, c = map(int, input().split())
edges.append([c, a, b])
edges.sort()
result = 0
for e in edges:
cost, a, b = e
if find(a) != find(b):
union(a, b)
result += cost
print(result)🧠아이디어
알고리즘 : 크루스칼 알고리즘
ℹ️크루스칼 알고리즘 정리(출처 - 이것이 취업을 위한 코딩테스트다 with 파이썬)
- 서로소 집합(Disjoint Sets) : 공통 원소가 없는 두 집합
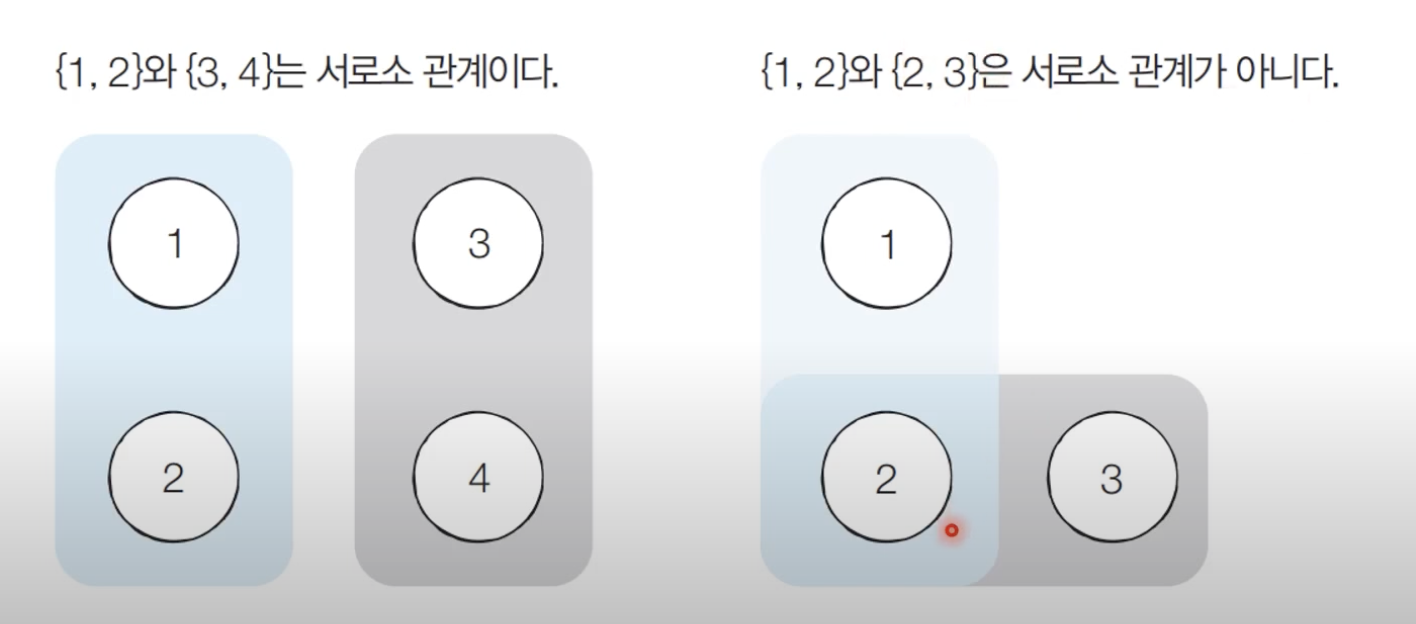
- 서로소 부분 집합들로 나누어진 원소들의 데이터를 처리하기 위한 자료구조
- 서로소 집합 자료구조에서 지원하는 연산 : Union(합집합) & Find(찾기)
- Find : 특정한 원소가 속한 집합이 어떤 집합인지
- Union : 두 개의 원소가 포함된 집합을 하나의 집합으로 합치는 연산
Find(): 특정 원소가 속한 집합을 찾기 / 루트 노드를 찾을 때까지 재귀 호출Union(): 두 원소가 속한 집합을 합치기
- 크루스칼 알고리즘
- 그래프에서 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프
- 모든 노드가 포함되어 서로 연결되면서 사이클이 존재하지 않는다는 조건
- 최소한의 비용으로 구성되는 신장 트리
- 간선 데이터를 비용에 따라 오름차순으로 정렬
- 간선을 하나씩 확인하면서 현재 간선이 사이클을 발생시키는지 확인한다.
- 현재 간선이 사이클을 발생시킨다면 포함시키지 않는다.
- 현재 간선이 사이클을 발생시키지 않는다면 포함시킨다.