💡문제접근
- 병든 나이트가 이동할 수 있는 최대 칸의 개수를 구하는 문제로 각각의 경우를 모두 나누어 따진 후 분기문을 작성했다.
Ex. N = 1(세로의 길이가 1인 경우)

- 시작점에서 이동할 수 있는 방법이 없으므로 답은 1이다.
Ex. N = 2(세로의 길이가 2인 경우)

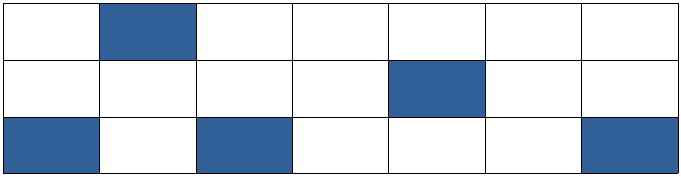
- 아래의 그림은 세로의 길이가 2고 가로의 길이가 9인 그림이다.
- 가로의 길이가 1~2인 경우 답은 1이다.
- 가로의 길이가 3~4인 경우 답은 2이다.
- 가로의 길이가 5~6인 경우 답은 3이다.
- 규칙을 찾으면 가로의 길이가 M인 경우 나올 수 있는 방법의 경우는
(M-1) // 2 + 1이다. 하지만 방문하는 칸의 개수가 5칸 이상이 나오는 경우라면 가로의 길이가 최소 9이상이어야 하고 가로의 길이가 7이면 나올 수 있는 최댓값은 4가 된다. 따라서 min을 사용해서 최솟값을 구하면 된다.
Ex. M < 7인 경우
- 가로의 길이가 7인 경우 방문할 수 있는 칸의 최대 개수는 5가 된다. 따라서 가로의 길이가 7보다 작은 경우는 최댓값이 4가 나올 수 밖에 없고 그 이상의 가로의 값이 나오는 경우 역시 최댓값은 4가 나오게 된다.
💡코드(메모리 : 31256KB, 시간 : 44ms)
import sys
input = sys.stdin.readline
N, M = map(int, input().strip().split())
if N == 1:
tot = 1
elif N == 2:
tot = min(4, (M-1) // 2 + 1)
elif M < 7:
tot = min(M, 4)
else:
tot = 2 + (M - 5) + 1
print(tot)
💡소요시간 : 51m



