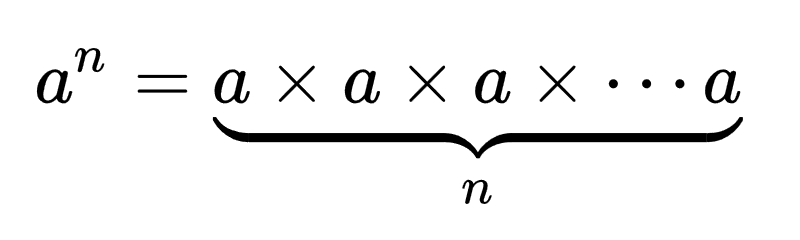[백준] 1629번 곱셈

• 거듭제곱이란?

• 똑같은 수나 문자를 여러 번 곱하는 것을 거듭제곱이라고 한다.
• 거듭제곱을 구하는 방법은 여러 가지가 있다. 각각의 방법을 모두 이해하고 어떤 코드가 가장 효율적인 코드인지를 이해하는 시간을 가지려고 한다.

• [반복문 사용]

• 예를 들어, a의 n제곱 값을 구하고 싶을 때, for문을 사용해 직관적으로 아래와 같은 코드를 작성할 수 있다.
• 반복문을 최대 n번 사용하므로 시간복잡도를 나타낸다면 O(N)이 된다.

def power(a, n):
	ans = 1
    for _ in range(n):
    	ans *= a
    return ans

• [재귀함수 사용]

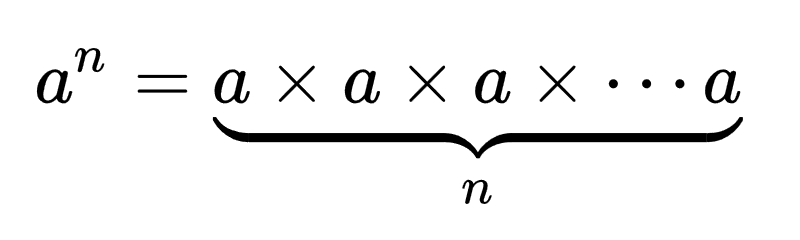
• 위 식은 부분문제로 나눌 수 있다. a의 n+1제곱은 a * a^n가 된다. 이를 이용해서 재귀함수를 작성하면 아래와 같다.
• 역시 마찬가지로 함수를 n번 호출하므로 아래 코드의 시간복잡도는 O(N)이 된다.

def recursive_power(a, n):
	if n == 1:
    	return a
    return recursive_power(a, n-1) * a

• [분할정복]

• 위의 방법들의 시간복잡도는 O(N)이다. 하지만 분할정복을 잘 사용한다면 O(log N)의 시간복잡도를 가지는 거듭제곱 연산 코드를 작성할 수 있다.

def power(a, n):
    if n == 0:
        return 1
    elif n == 1:
    	return a
        
    x = power(a, n//2)	# 재귀로 처리하는 방식을 피하기 위해 똑같은 값이 나오는 power(a, n//2)를 미리 구해 변수에 할당
    if n % 2 == 0:
        return x * x
    else:
        return x * x * a

💡문제접근

• 분할정복을 통한 거듭제곱, 반복문, 재귀함수 호출 등 각각의 방법으로 코드를 작성할 경우 얻어지는 시간복잡도에 대해서 공부할 수 있는 시간을 가지게 해 준 문제
• a^n = a^n//2 * a^n//2 → 짝수
• a^n = a^n//2 * a^n//2 * a → 홀수

💡코드(메모리 : 31256KB, 시간 : 40ms)

import sys
input = sys.stdin.readline

A, B, C = map(int, input().strip().split())

def power(a, b, c):
    if b == 0:
        return 1
    elif b == 1:
        return a % c

    temp = power(a, b//2, c)
    if b % 2 == 0:
        return temp * temp % c
    else:
        return temp * temp * a % c

print(power(A, B, C))

💡소요시간 : 1h