[C] 백준 2357번 최솟값과 최댓값

김진웅·2024년 1월 18일

baekjoon-study

목록 보기

58/59

문제

N(1 ≤ N ≤ 100,000)개의 정수들이 있을 때, a번째 정수부터 b번째 정수까지 중에서 제일 작은 정수, 또는 제일 큰 정수를 찾는 것은 어려운 일이 아니다. 하지만 이와 같은 a, b의 쌍이 M(1 ≤ M ≤ 100,000)개 주어졌을 때는 어려운 문제가 된다. 이 문제를 해결해 보자.

여기서 a번째라는 것은 입력되는 순서로 a번째라는 이야기이다. 예를 들어 a=1, b=3이라면 입력된 순서대로 1번, 2번, 3번 정수 중에서 최소, 최댓값을 찾아야 한다. 각각의 정수들은 1이상 1,000,000,000이하의 값을 갖는다.

입력

첫째 줄에 N, M이 주어진다. 다음 N개의 줄에는 N개의 정수가 주어진다. 다음 M개의 줄에는 a, b의 쌍이 주어진다.

출력

M개의 줄에 입력받은 순서대로 각 a, b에 대한 답을 최솟값, 최댓값 순서로 출력한다.

예제 입력 1

예제 출력 1

아이디어 스케치

세그먼트 트리 자료구조를 이용하여 푸는 문제이다.

이 문제에서는 주어진 범위에서의 최댓값과 최솟값을 구해 출력해야하므로, 최댓값 세그먼트 트리와 최솟값 세그먼트 트리 2개를 이용해야 한다.

값을 입력 받기 전 세그먼트 트리의 크기를 정해야한다. 트리의 크기를 정하는 기준은 입력 받는 숫자의 개수 N을 기준으로 N보다 같거나 큰 2의 지수승 중에서 가장 작은 값 k에 2를 곱한 값을 크기로 정한다.

예제에서는 10개의 수를 입력 받았으므로 10과 같거나 큰 2의 지수승인 16에 2를 곱한 32를 트리의 크기로 설정한다.

트리의 크기만큼 동적할당을 받은 후, N개의 숫자를 입력 받는다. 이때 입력 받는 숫자는 트리의 리프노드에 순서대로 집어 넣어야 한다. 따라서 리프노드의 인덱스를 구해야 하는데, 위에서 구한 N보다 같거나 큰 2의 지수승 중에서 가장 작은 값인 16이 리프노드의 시작 인덱스이다. 따라서 16부터 16+N인덱스까지 값을 입력받으면 된다.

리프노드의 값을 입력 받은 후 트리의 루트노드 까지 값을 채워야 하는데, 최댓값 세그먼트 트리는 두 개의 자식 노드 중 더 큰 값을 부모 노드의 값으로 저장하고, 최솟값 세그먼트 트리는 두 개의 자식 노드 중 더 작은 값을 부모 노드의 값으로 저장한다.

세그먼트 트리를 배열로 선언하였을 때, 부모 노드의 인덱스에 2를 곱한 값과 2를 곱한 값에 1을 더한 값이 각각 좌측 자식노드의 인덱스, 우측 자식노드의 인덱스에 해당된다. 점화식으로 표현하면 다음과 같다.

tree[i]의 자식노드 tree[ix2], tree[ix2+1]

위 점화식을 조금 변형하여 최댓값 세그먼트 트리와 최솟값 세그먼트 트리의 노드들을 채울 수 있다.

먼저 최댓값 세그먼트 트리는 두 개의 자식 노드 중 더 큰 값을 부모 노드가 가지므로
tree[i] = max(tree[ix2], tree[ix2+1])
로 나타낼 수 있고,

최솟값 세그먼트 트리는 두 개의 자식 노드 중 더 작은 값을 부모 노드가 가지므로
tree[i] = min(tree[ix2], tree[ix2+1])
으로 나타낼 수 있다.

예제 입력을 이용하여 트리를 초기화 한 걸 그림으로 나타내면

최댓값 세그먼트 트리

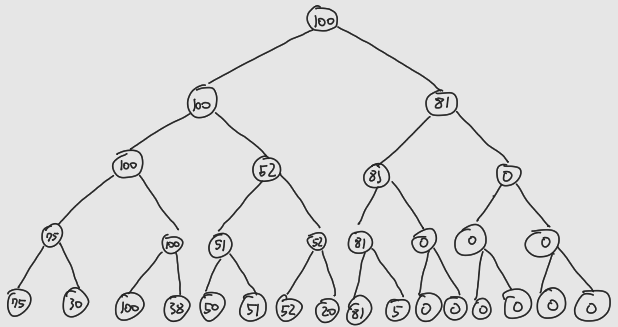
최솟값 세그먼트 트리

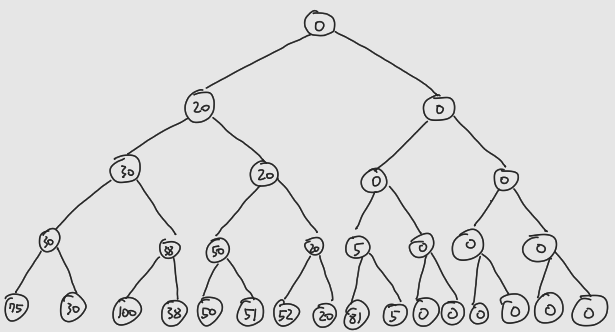
위와 같다.

트리를 완성했으면 이제 문제에서 주어지는 a와 b를 이용하여 그 범위 해당하는 최솟값과 최댓값을 구해야 한다.

a와 b는 각각 입력된 순서를 나타내므로 각 숫자를 리프노드의 인덱스로 변환하는 과정을 거쳐야 한다.

a는 a+(리프노드의 시작인덱스-1), b는 b+(리프노드의 시작인덱스-1)로 변환한 후 각각 start, end로 정의한다.

최댓값을 구하는 과정부터 살펴보면
start가 홀수, 즉 부모 노드 기준으로 우측에 위치한 경우에는 이 노드의 부모노드를 탐색할 필요가 없다. 그 이유는 좌측 자식 노드가 구하려는 범위에 포함되어 있지 않기 때문에 부모 노드를 포함하게 되면 좌측 자식 노드의 값에 따라 다른 결과를 나타낼 수 있기 때문이다. 따라서 이 경우에는 우측 자식 노드의 값과 현재까지 구한 최댓값을 비교한 후 최댓값을 갱신한다. 이후 현재 start인덱스에 1을 더한 후 2로 나눔으로써 기존 부모노드의 다음 노드를 start 노드로 갱신한다.

end가 짝수, 즉 부모 노드 기준으로 좌측에 위치한 경우에는 이 노드의 부모노도를 탐색할 필요가 없다. 그 이유는 우측 자식 노드가 구하려는 범위에 포함되어 있지 않기 때무네 부모 노드를 포함하게 되면 우측 자식 노드의 값에 따라 다른 결과를 나타낼 수 있기 때문이다. 따라서 이 경우에는 좌측 자식 노드의 값과 현재까지 구한 최댓값을 비교한 후 최댓값을 갱신한다. 이후 현재 end인덱스에 1을 뺀 후 2로 나눔으로써 기존 부모노드의 이전 노드를 end 노드로 갱신한다.

위 과정을 start노드와 end노드가 뒤집힐 때까지 반복한다.

최솟값을 구하는 과정은 최댓값이라는 단어가 들어가는 부분을 최솟값으로 바꾸면 된다.

전체 코드

#include <stdio.h>
#include <stdlib.h>

#define max(a, b) a > b ? a : b
#define min(a, b) a > b ? b : a

int tree_size = 1;
int* max_tree;		// 최댓값 세그먼트 트리
int* min_tree;		// 최솟값 세그먼트 트리

// 함수 헤더 선언
int search_min(int a, int b);
int search_max(int a, int b);

int main()
{
	
	int N, M;
	int input;
	int a, b;

	scanf("%d %d", &N, &M);

	// 입력받는 숫자의 개수보다 크면서 가장 유사한 2의 지수승 값을 찾음
	while (tree_size < N) 
		tree_size *= 2;

	// tree_size*2 크기의 트리 동적할당
	max_tree = (int*)calloc(tree_size * 2, sizeof(int));
	min_tree = (int*)calloc(tree_size * 2, sizeof(int));

	for (int i = tree_size; i < tree_size + N; i++) {
		scanf("%d", &input);
		max_tree[i] = input, min_tree[i] = input;
	}

	for (int i = tree_size - 1; i >= 1; i--) {
		max_tree[i] = max(max_tree[i * 2], max_tree[i * 2 + 1]);	// max트리 값 초기화
		min_tree[i] = min(min_tree[i * 2], min_tree[i * 2 + 1]);	// min트리 값 초기화
	}

	while (M--) {
		scanf("%d %d", &a, &b);
		printf("%d %d\n", search_min(a, b), search_max(a, b));
	}

	// 메모리 해제
	free(min_tree);
	free(max_tree);

	return 0;

}

// 정해진 구역의 최댓값을 찾아 반환하는 함수
int search_max(int a, int b) {
	int start = a + tree_size - 1;	// a를 트리의 인덱스로 변환
	int end = b + tree_size - 1;	// b를 트리의 인덱스로 변환
	int max = 0;

	// start와 end가 뒤집어지기 전까지 반복
	while (start <= end) {
		if (start % 2 == 1) {		// start에 해당하는 노드가 부모노드 기준 우측 자식인 경우
			if (max < max_tree[start])	// 현재 max값과 비교 후 값을 갱신
				max = max_tree[start];
		}
		if (end % 2 == 0) {			// end에 해당하는 노드가 부모노드 기준 좌측 자식인 경우
			if (max < max_tree[end])	// 현재 max값과 비교 후 값을 갱신
				max = max_tree[end];
		}
		start = (start + 1) / 2;	// start가 우측 자식인 경우에는 부모 노드의 오른쪽 노드 선택, 좌측 자식인 경우에는 부모 노드 선택
		end = (end - 1) / 2;		// end가 좌측 자식인 경우에는 부모 노드의 왼쪽 노드 선택, 우측 자식인 경우에는 부모 노드 선택
	}

	return max;		// 결과값 반환
}

// 정해진 구역의 최솟값을 찾아 반환하는 함수
int search_min(int a, int b) {
	int start = a + tree_size - 1;	// a를 트리의 인덱스로 변환
	int end = b + tree_size - 1;	// b를 트리의 인덱스로 변환
	int min = min_tree[start];		// 최솟값을 start 인덱스에 해당하는 값으로 초기화

	// start와 end가 뒤집어지기 전까지 반복
	while (start <= end) {
		if (start % 2 == 1) {		// search_max 함수 설명과 같음
			if (min > min_tree[start])
				min = min_tree[start];
		}
		if (end % 2 == 0) {
			if (min > min_tree[end])
				min = min_tree[end];
		}
		start = (start + 1) / 2;
		end = (end - 1) / 2;
	}

	return min;
}