[C] 백준 1991번 트리 순회

링크
https://www.acmicpc.net/problem/1991

문제

---

이진 트리를 입력받아 전위 순회(preorder traversal), 중위 순회(inorder traversal), 후위 순회(postorder traversal)한 결과를 출력하는 프로그램을 작성하시오.

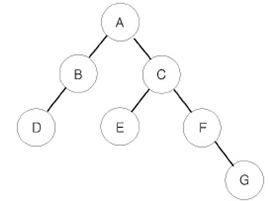
예를 들어 위와 같은 이진 트리가 입력되면,

• 전위 순회한 결과 : ABDCEFG // (루트) (왼쪽 자식) (오른쪽 자식)
• 중위 순회한 결과 : DBAECFG // (왼쪽 자식) (루트) (오른쪽 자식)
• 후위 순회한 결과 : DBEGFCA // (왼쪽 자식) (오른쪽 자식) (루트)

가 된다.

입력

---

첫째 줄에는 이진 트리의 노드의 개수 N(1 ≤ N ≤ 26)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 노드와 그의 왼쪽 자식 노드, 오른쪽 자식 노드가 주어진다. 노드의 이름은 A부터 차례대로 알파벳 대문자로 매겨지며, 항상 A가 루트 노드가 된다. 자식 노드가 없는 경우에는 .으로 표현한다.

출력

---

첫째 줄에 전위 순회, 둘째 줄에 중위 순회, 셋째 줄에 후위 순회한 결과를 출력한다. 각 줄에 N개의 알파벳을 공백 없이 출력하면 된다.

예제 입력 1

---

7
A B C
B D .
C E F
E . .
F . G
D . .
G . .

예제 출력 1

---

ABDCEFG
DBAECFG
DBEGFCA

아이디어 스케치

---

트리 순회란 특정 목적을 위해 트리의 모든 노드를 한 번씩 방문하는 것을 말한다.
트리 구조는 계층적 구조라는 특별한 특징을 가지기 때문에,모든 노드를 순회하는 방법엔 크게 세 가지가 있다.
트리를 순회할 수 있는 세 가지 방법은 전위 순회, 중위 순회, 후위 순회가 있다.

전위 순회의 방문 순서
루트 -> 왼쪽 자식 -> 오른쪽 자식

중위 순회의 방문 순서
왼쪽 자식 -> 루트 -> 오른쪽 자식

후위 순회의 방문 순서
왼쪽 자식 -> 오른쪽 자식 -> 루트

위와 같이 트리에서의 순회 방식은 항상 왼쪽부터 이루어진다.

전체 코드

---

#include <stdio.h>

int arr[27][2];

// 전위 순회
void preorder(int n) {
	if (n == -1) return;
	printf("%c", n + 'A');	// 루트
	preorder(arr[n][0]);	// 왼쪽 자식
	preorder(arr[n][1]);	// 오른쪽 자식
}

// 중위 순회
void inorder(int n) {
	if (n == -1) return;
	inorder(arr[n][0]);		// 왼쪽 자식
	printf("%c", n + 'A');	// 루트
	inorder(arr[n][1]);		// 오른쪽 자식
}

// 후위 순회
void postorder(int n) {
	if (n == -1) return;
	postorder(arr[n][0]);	// 왼쪽 자식
	postorder(arr[n][1]);	// 오른쪽 자식
	printf("%c", n + 'A');	// 루트
}

int main()
{
	int N;			// 노드의 개수
	char x, y, z;	// 노드, 왼쪽 자식 노드, 오른쪽 자식 노드

	scanf("%d", &N);

	for (int i = 0; i < N; i++) {
		scanf(" %c %c %c", &x, &y, &z);
		x = x - 'A';	// 숫자로 변환
		if (y == '.') arr[x][0] = -1;	// 자식 없음
		else arr[x][0] = y - 'A';	// 숫자로 변환

		if (z == '.') arr[x][1] = -1;	// 자식 없음
		else arr[x][1] = z - 'A';	// 숫자로 변환
	}

	preorder(0);	// 전위 순회
	printf("\n");	
	inorder(0);		// 중위 순회
	printf("\n");
	postorder(0);	// 후위 순회

	return 0;
}

제출 결과

---