링크
https://www.acmicpc.net/problem/11057
문제
오르막 수는 수의 자리가 오름차순을 이루는 수를 말한다. 이때, 인접한 수가 같아도 오름차순으로 친다.
예를 들어, 2234와 3678, 11119는 오르막 수이지만, 2232, 3676, 91111은 오르막 수가 아니다.
수의 길이 N이 주어졌을 때, 오르막 수의 개수를 구하는 프로그램을 작성하시오. 수는 0으로 시작할 수 있다.
입력
첫째 줄에 N (1 ≤ N ≤ 1,000)이 주어진다.
출력
첫째 줄에 길이가 N인 오르막 수의 개수를 10,007로 나눈 나머지를 출력한다.
예제 입력 1
1예제 출력 1
10예제 입력 2
2예제 출력 2
55에제 입력 3
3예제 출력 3
220아이디어 스케치
문제의 조건을 살펴보면,
오르막 수는 오름차순을 이루는 수로, 인접한 수가 같아도 오름차순으로 친다.
수는 0으로 시작할 수 있다.
각 수의 끝자리 별로 문제에서 제시한 조건을 만족하는 수의 개수를 살펴보면
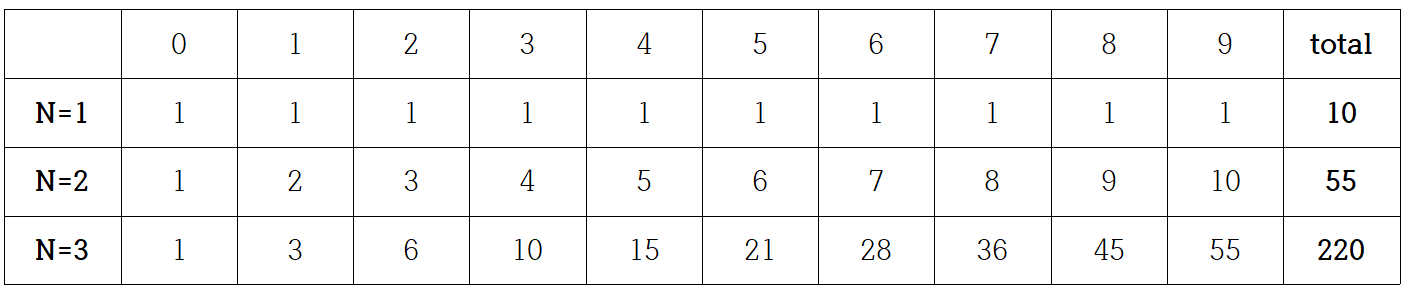
위와 같다.
이때 N은 수의 길이를 나타낸다.
N=1, 즉 길이가 1일 때 끝자리가 0~9인 경우 각각 1개의 경우의 수를 가지고 총 10개의 경우의 수를 가진다.
N=2 일 때,
끝자리가 0인 경우
00 (1가지)
끝자리가 1인 경우
01, 11 (2가지)
끝자리가 2인 경우
02, 12, 22 (3가지)
0~9는 각각 1~10개의 경우의 수를 가지고 총 55개의 경우의 수를 가진다.
위 표에서 한가지 규칙을 도출해낼 수 있다.
N이 i이고, 끝자리가 j일 때의 경우의 수는 N이 i-1이고 끝자리가 0부터 j까지의 경우의 수의 합과 같다는 것을 알 수 있다.
경우의 수를 저장하는 배열을 dp라고 정의했을 때, 점화식을 구해보면
dp[i][j] = dp[i-1][0] + dp[i-1][1] + ... + dp[i-1][j]
이다.
전체 코드
#include <stdio.h>
int main()
{
int N;
int dp[1001][10] = { 0, };
int sum = 0;
scanf("%d", &N);
for (int i = 0; i < 10; i++)
dp[1][i] = 1; // N=1일 때 자릿수별로 경우의 수를 1개씩 가짐
for (int i = 2; i <= N; i++) {
for (int j = 0; j < 10; j++) {
for (int k = 0; k <= j; k++) {
dp[i][j] += dp[i - 1][k] % 10007; // N=i일 때 N[i][j]의 값은 N[i-1][0~j까지의 합]을 가짐
}
}
}
for (int i = 0; i < 10; i++)
sum += dp[N][i] % 10007; // N행의 경우의 수의 합을 구함
printf("%d", sum % 10007); // 결과 출력
return 0;
}제출 결과


