[Python] 스택(Stack)

ITmakesmeSoft·2022년 9월 25일

algorithm python stack 스택

Algorithm_기초

목록 보기

4/7

위키백과

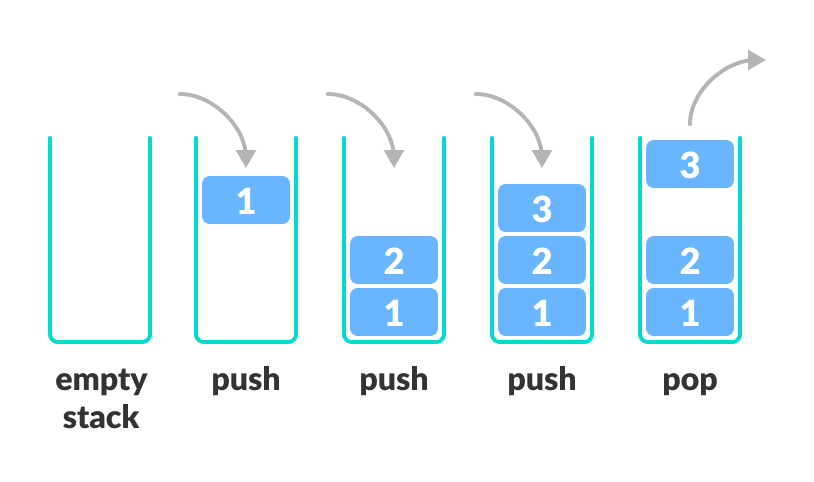
물건을 쌓아 올리듯 자료를 쌓아 올린 후입선출(LIFO, Last-In-First-Out)형태의 자료구조
- FIFO(선입선출) : 먼저 삽입한 자료를 먼저 꺼내는 방식(ex. Stack)
  - LIFO(후입선출) : 가장 나중에 꺼낸 자료부터 꺼내는 방식(ex. Queue)
스택에 저장된 자료는 선형 구조를 가짐
- 선형 구조 : 자료 간의 관계가 1:1의 관계
- 비선형 구조 : 자료 간의 관계가 1:N의 관계 (Ex. 트리)

스택의 구현

https://images.app.goo.gl/aei6cALjvUhK2WN86

자료 구조 : 자료를 선형으로 저장할 저장소
- 배열 사용
- 저장소 자체를 스택이라 부름
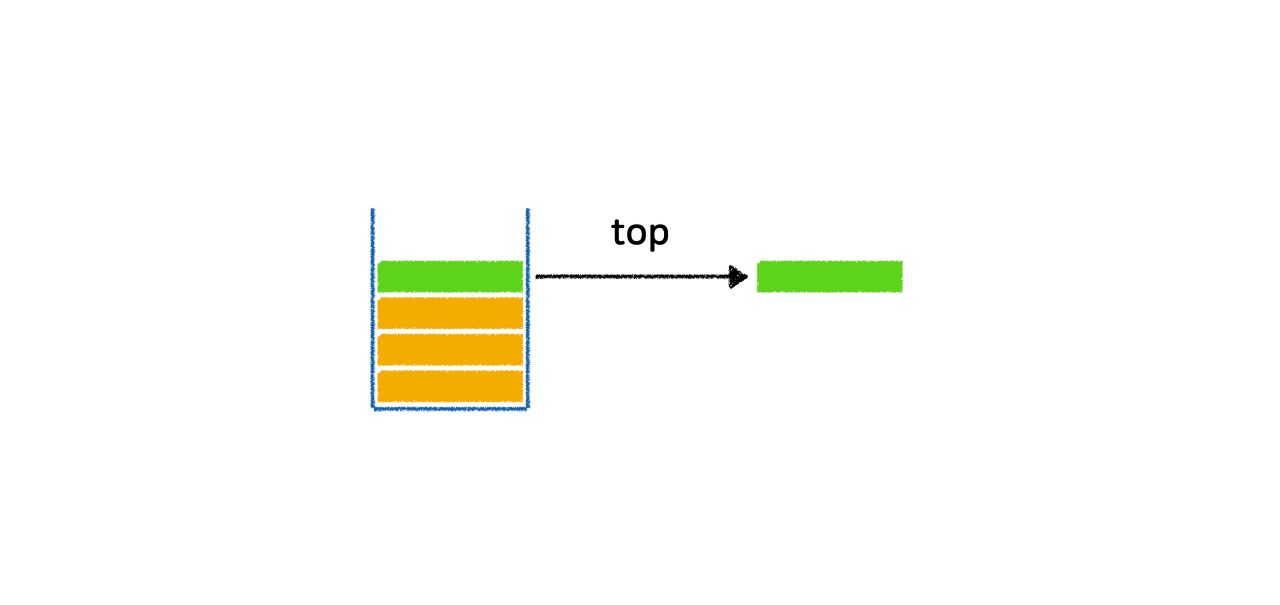
- 스택에서 마지막 삽입된 원소의 위치를 top이라 함
일반적으로 스택에서 사용되는 연산
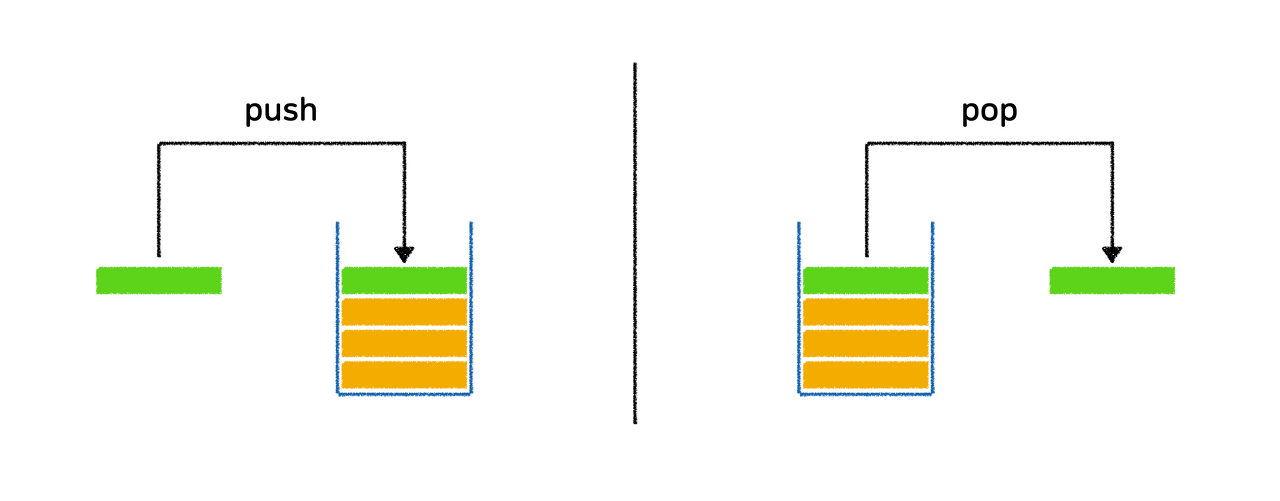
- push : 저장소에 자료 저장
- pop : 저장소에 삽입한 자료의 역순(마지막 삽입한 자료부터)으로 원소를 반환하고 스택에서 삭제
  
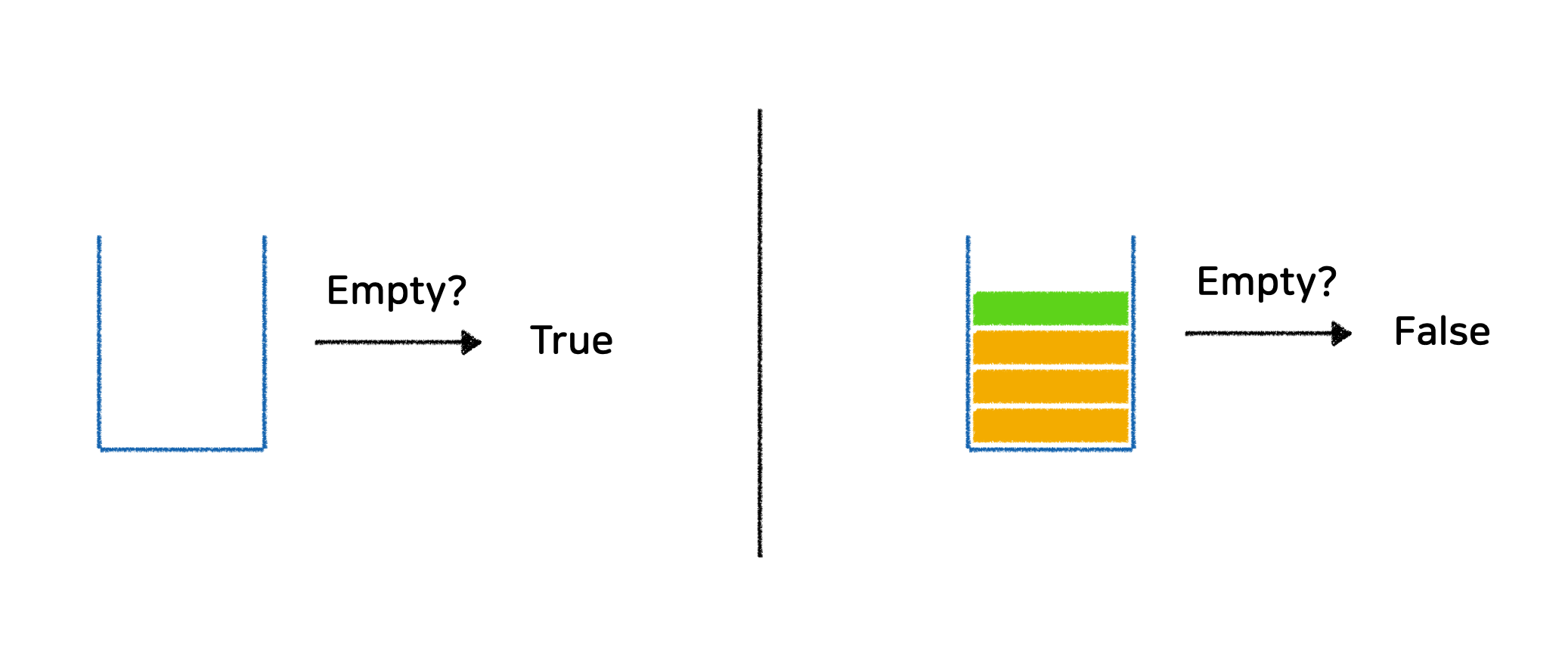
  파이썬으로-구현하는-자료구조-스택-Stack
- isEmpty : 스택이 공백인지 아닌지를 확인하는 연산
  
  파이썬으로-구현하는-자료구조-스택-Stack
- peek(또는 top) : 가장 마지막에 삽입한 데이터를 삭제하지 않고 return (↔pop과 차이)
  
  파이썬으로-구현하는-자료구조-스택-Stack

Stack Overflow

프로그램 호출 stack에서 이용 가능한 공간 이상을 사용하는 경우, stack overflow가 발생

스택의 구현

class Stack():
    def __init__(self):
        self.stack = []

    def push(self, data):
        self.stack.append(data)
    
    def pop(self):
        if self.isEmpty():
            print("stack is empty")
        else:
            return self.stack.pop()
    
    def peek(self):
        if self.isEmpty():
            print('stack is empty')
        else:
            self.stack[-1]
        
    def isEmpty(self):
        if len(self.stack) == 0:
            return True
        else:
            return False

스택의 활용

괄호 검사

중위 표기법(Infix Notation)

연산자를 두 피연산자 사이에 표기하는 방법
가장 일반적으로 사용되는 표현법 ex) A+B

전위 표기법(Prefix Notation)

연산자를 먼저 표기하고 피연산자를 나중에 표기하는 방법 ex) +AB
중위 표기법 → 전위 표기법 변환
1. 연산자의 우선순위에 따라 괄호 표기
2. 괄호 안에 있는 각 연산자들을 왼쪽 괄호 앞으로 이동
3. 괄호 제거
  
  ex) A*B-C/D
  - ((A*B)-(C/D))
  - -(*(A B)/(C D))
  - -*AB/CD

후위 표기법(Postfix Notation)

피연산자를 먼저 표기하고 연산자를 나중에 표기하는 방법
컴파일러가 사용하는 것으로, 스택을 이용하는 경우 빈번하게 사용 ex) AB+
중위 표기법 → 후위 표기법 변환 방법
1. 수식의 각 연산자에 대해 우선순위에 따라 괄호 표기
2. 괄호 안에 있는 각 연산자들을 오른쪽 괄호 뒤로 이동
3. 괄호 제거
  
  ex) A*B-C/D
  - ((A*B)-(C/D))
  - ((A B)* (C D)/)-
  - AB*CD/-

백트래킹

백트래킹(Backtracking) 기법은 해를 찾는 도중에 막히면(해가 아닌 경우) 되돌아가서 다시 해를 찾아가는 기법
백트래킹 기법은 최적화(Optimization) 문제와 결정(Decision) 문제를 해결할 수 있음
상태 공간 트리의 깊이 우선 탐색(DFS)을 실시
각 노드의 유망성(해답이 될 가능성)을 점검한 후, 유망(promising)하지 않다고 결정되면 그 노드의 부모로 되돌아가(Backtracking) 다음 자식 노드로 이동
가지치기(pruning) : 유망하지 않는 노드가 포함되는 경로는 더 이상 고려하지 않음.
- 결정문제 : 문제의 조건을 만족하는 해가 존재하는지의 여부를 yes, 또는 no가 답하는 문제
  - 미로찾기
  - n-Queen 문제
  - Map coloring
  - 부분 집합의 합(Subset Sum) 문제 등