[Python] 동적계획법(DP, Dynamic Programming)

Dynamic Programming?
DP의 창시자에 따르면, 다이나믹 프로그래밍이라는 이름은 연구비 예산을 위해서 적당한 이름을 찾다가 나온 것이라고…

동적 계획법(DP, Dynamic Programming)

• 입력 크기가 작은 부분을 모두 해결한 후, 그 해들을 이용하여 보다 큰 크기의 무제들을 해결, 최종적으로 주어진 입력의 문제를 해결하는 알고리즘.
• 그리디 알고리즘과 같이 최적화 문제를 해결하는 알고리즘
• 즉, 문제를 작은 부분으로 나누고, 겹치는 부분 문제들은 한 번만 계산 한 뒤, 그 결과를 저장하여 나중의 큰 문제를 풀때 재사용하는 방식 = 기억하며 풀기

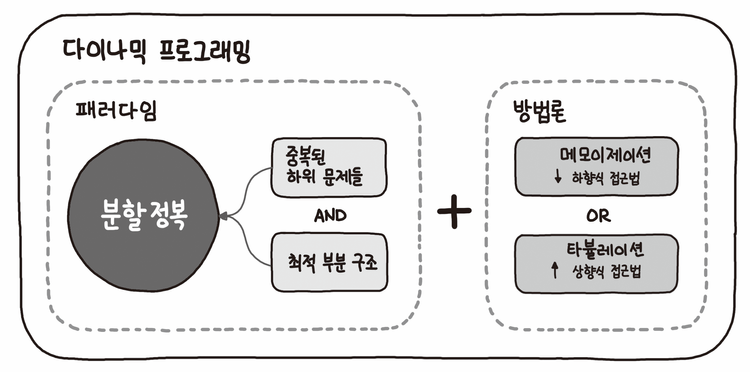
이미지 출처 : 파이썬 알고리즘 인터뷰(책만 출판사)

DP의 접근 방법에 따른 구현 방식

Top - Down 방식

• 일부 부분 문제의 연산으로도 최종 결과를 얻을 수 있는 경우
• 재귀(Recursive) - memoization 이용
  • memoization : 함수의 반환 값을 저장하여 이 후의 같은 연산이 생길 경우 저장된 값을 사용하는 것

Bottom - Up 방식

• 모든 부분 문제의 연산이 있어야 최종 결과를 얻을 수 있는 경우
• 반복(Iterative) - tabulation 이용
  • tabulation : 작은 부분문제부터 시작하여 최종 문제의 결과를 도출할 때까지 결과값을 차례대로 기록하는 것

DP를 쓰는 이유

• 일반적인 재귀를 단순히 사용하는 경우, 동일한 부분 문제를 반복적으로 계산하기 때문에 크기가 커질 수록 매우 비효율적임.
• 이 경우 DP를 통해 문제 해결 시 효율을 극대화할 수 있음
• 피보나치 수열 비교 예시
  • 피보나치 수 재귀 이용 - $O(2^n)$

    def fibonacci(n):
    		if n <= 1:
    				return n
    		return fibonacci(n-1) + fibonacci(n-2)

  • 피보나치 수 DP 이용 - $O(n)$

    def fibonacci(n):
    		f = [0, 1]
    
    		for i in range(2, n+1):
    				f.append(f[i-1] + f[i-2])
    
    		return f[n]

  • 연산 횟수 비교

    	Recursive(재귀) 방식	DP 방식
    fibonacci(3)	5	2
    fibonacci(10)	177	9
    fibonacci(20)	21891	19
    fibonacci(30)	2692537	29

    • 숫자가 커질 수록 연산 횟수는 기하급수적으로 증가

DP의 사용 조건

• Overlapping Subproblems(겹치는 부분 문제)
  • 동일한 부분 문제들이 여러번 반복하여 나타나는 경우
• Optimal Substructure(최적의 부분 구조)
  • 부분 문제의 결과값을 이용하여 전체 문제의 최적의 해를 구할 수 있는 경우