
문제링크
https://programmers.co.kr/learn/courses/30/lessons/42898
문제
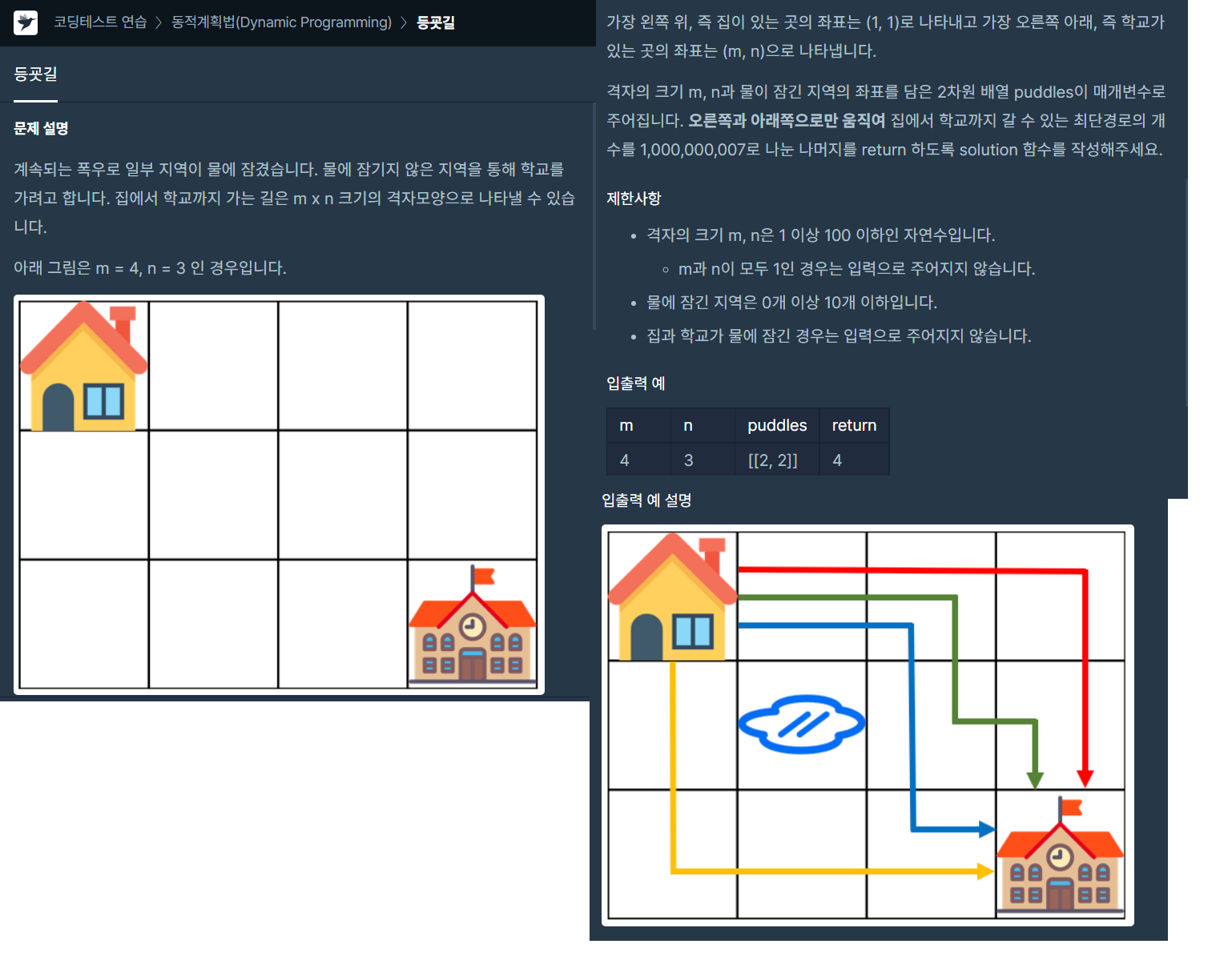
분류
-
알고리즘 분류
동적 계획법 -
난이도
프로그래머스 Level 3 -
사용 언어
java
코드
try 1
경우의 수 계산
어떻게 가더라도 조건대로 움직이면 최소 동선이기에
다음과 같이 찾으려고 했다.
웅덩이를 피한 집에서 학교로 가는 경우의 수 = 집에서 학교로 가는 경우의 수 -
(집에서 웅덩이로 가는 경우의수 + 웅덩이에서 학교로 가는 경우의수)지도의 크기와 총 경우의 수가 관계가 있기에 이를 규명할 공식을 찾아내려했다.
크기가 (4,3) 일때 총 경우의 수
1 + 2 + 3 + 4 = 10
크기가 (3,4) 일때 총 경우의 수
1 + 3 + 6 = 10
크기가 (4,4) 일때 총 경우의 수
1 + 3 + 6 + 10 = 20
크기가 (5,3) 일때 총 경우의 수
1 + 2 + 3 + 4 + 5 = 15
크기가 (5,4) 일때 총 경우의 수
1 + 3 + 6 + 10 + 15 = 35
크기가 (6,4) 일때 총 경우의 수
1 + 3 + 6 + 10 + 15 + 21 = 56
크기가 (4,5) 일때 총 경우의 수
1 + 4 + 10 + 20 = 35
크기가 (4,6) 일때 총 경우의 수
1 + 5 + 15 + 35 = 56
결과
여러개 테스트를 해봤지만 우둔한 내 머리로는 이렇다할 점화식을 만들지 못하고 다른 방법을 생각 해보기로 한다.
걸린 시간
문제 이해 포함 약 한시간
try 2
타일마다 경우의 수 저장
해당 타일에서 학교까지 가는 경우의 수는
오른쪽으로 가는 경우의 수 + 아래로 가는 경우의 수 다음 그림과 같다
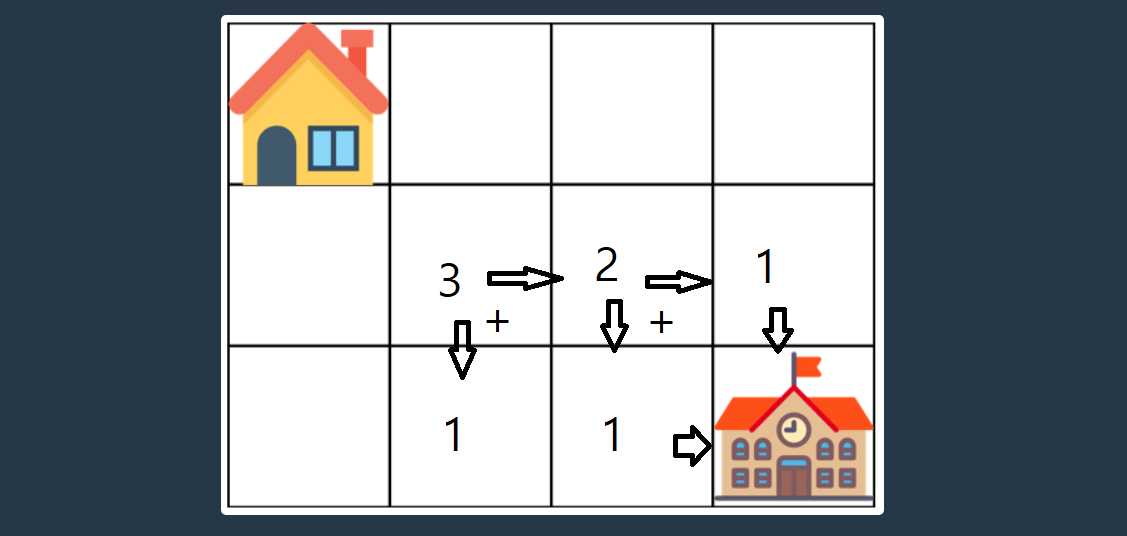
이를 이용해 총 경우의 수 - 웅덩이에서 학교까지 가는 경우의 수를 빼보기로 한다.
코드
class Solution {
public int solution(int m, int n, int[][] puddles) {
int answer = 0;
int [][] tileCase = new int[n][m]; // m은 x좌표, n은 y좌표이기에
// 각 타일의 경우의 수 초기화
for(int i=n-1; i>=0; i--) {
for(int j=m-1; j>=0; j--) {
// 아래로 갈 수 없거나 오른쪽으로 갈 수 없을 경우 경우의 수는 하나
if(i == n-1 || j == m-1) {
tileCase[i][j] = 1;
}else{
tileCase[i][j] = tileCase[i+1][j] + tileCase[i][j+1];
}
}
}
// 총 경우의 수 - 웅덩이 타일에서의 경우의 수
for(int i=0; i<puddles.length; i++){
// 웅덩이의 좌표 표시를 index로 표현하기 위해 x,y 각각 -1을 함
tileCase[0][0] -= tileCase[puddles[i][1] - 1][puddles[i][0] - 1];
}
answer = tileCase[0][0] % 1000000007;
return answer;
}
}결과
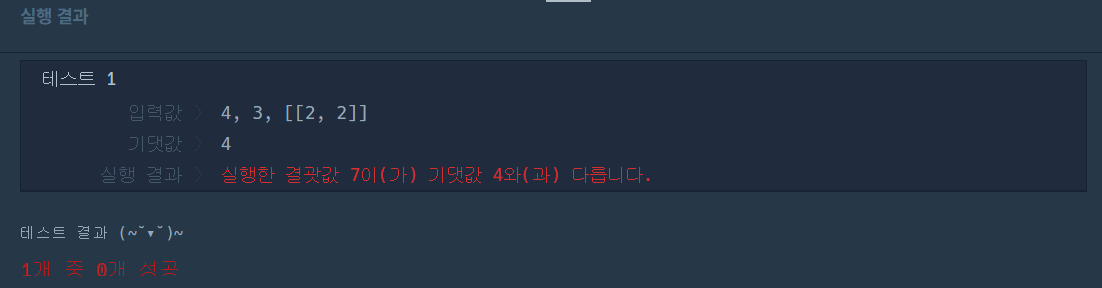
테스트도 통과하지 못하였다.
걸린 시간
약 30분
try 3
타일 초기화 간 웅덩이 타일 제외
이전 시도의 패인이 총 경우의 수 - 웅덩이 타일의 경우의 수를 했는데
이렇게 하면 초기화 진행간에 이미 웅덩이 타일을 지나는 경우의 수를 더해버리게 된다.
해서 초기화 진행간에 오른쪽이나 밑에 웅덩이 타일이 있다면 이를 제외한다. 따라서 마지막의 웅덩이 타일을 제외하는 계산 부분은 지워지게된다.
코드
class Solution {
public int solution(int m, int n, int[][] puddles) {
int answer = 0;
int [][] tileCase = new int[n][m]; // m은 x좌표, n은 y좌표이기에
// 각 타일의 경우의 수 초기화
for(int i=n-1; i>=0; i--) {
for(int j=m-1; j>=0; j--) {
// 아래로 갈 수 없거나 오른쪽으로 갈 수 없을 경우 경우의 수는 하나
if(i == n-1 || j == m-1) {
tileCase[i][j] = 1;
}else{
tileCase[i][j] = 0;
// 오른쪽 or 아래가 웅덩이라면 그 부분 제외
for(int k=0; k<puddles.length; k++) {
if(j+1 == puddles[k][0] - 1 &&
i == puddles[k][1] - 1) { // 오른쪽이 웅덩이라면
// 공통적인 처리를 위해 값만 제외하고 진행
tileCase[i][j] -= tileCase[i][j+1];
}if(i+1 == puddles[k][1] - 1 &&
j == puddles[k][0] - 1) { // 아래가 웅덩이라면
tileCase[i][j] -= tileCase[i+1][j];
}
}
tileCase[i][j] += tileCase[i+1][j] + tileCase[i][j+1];
}
}
}
answer = tileCase[0][0] % 1000000007;
return answer;
}
}결과
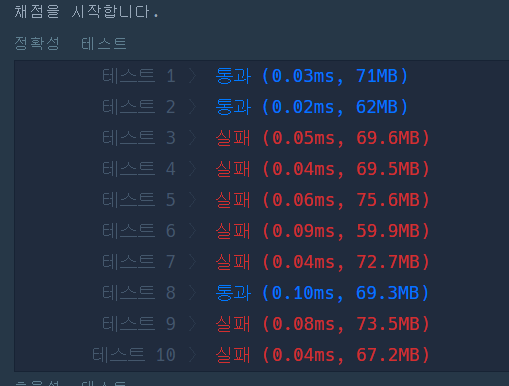
걸린 시간
약 30분
try 4
웅덩이 타일 초기화
한 타일의 경우의 수를 구할 때마다 웅덩이타일인지 모두 검사했는데,
비효율적이라 판단해서 -1로 flag를 주고 확인한 이후에 0으로 초기화하는 방식으로 진행
위에서는 최단경로의 개수가 0이 나올 수 있음을 고려하지 않았음.
코드
class Solution {
public int solution(int m, int n, int[][] puddles) {
int answer = 0;
int [][] tileCase = new int[n][m]; // m은 x좌표, n은 y좌표이기에
// 웅덩이 타일 초기화
for(int i=0; i<puddles.length; i++) {
tileCase[puddles[i][1] - 1][puddles[i][0] - 1] = -1;
}
// 학교에서부터 출발하기에 1로 초기화
tileCase[n-1][m-1] = 1;
// 각 타일의 경우의 수 초기화
for(int i=n-1; i>=0; i--) {
for(int j=m-1; j>=0; j--) {
//웅덩이 타일일 경우
if(tileCase[i][j] == -1) {
tileCase[i][j] = 0;
}else{
// index out of bounds 방지
if(j != m-1) { // 오른쪽 타일 경우의 수 더하기
tileCase[i][j] += tileCase[i][j+1];
}if(i != n-1) { // 아래 타일 경우의 수
tileCase[i][j] += tileCase[i+1][j];
}
}
}
}
answer = tileCase[0][0] % 1000000007;
return answer;
}
}결과
정확성은 모두 맞았지만, 효율성에서는 모두 실패를 했다.
걸린시간
약 15분
try 5
1,000,000,007로 나눈 나머지
생각해보니 효율성면에서 시간초과가 아닌 실패로 떴기에 오류가 있음을 인지했다.
그래서 문제에 있는
최단경로의 개수를 1,000,000,007로 나눈 나머지를 return 하도록 solution 함수를 작성해주세요
를 보고 중간마다 계산되는 값이 너무 커서 오류가 났음을 인지했다.
원래 있던 코드에는 마지막에만 나머지를 구했다면 이를 중간 타일에도 적용을 시켜서 결과를 얻었다.
코드
class Solution {
public int solution(int m, int n, int[][] puddles) {
int answer = 0;
int [][] tileCase = new int[n][m]; // m은 x좌표, n은 y좌표이기에
// 웅덩이 타일 초기화
for(int i=0; i<puddles.length; i++) {
tileCase[puddles[i][1] - 1][puddles[i][0] - 1] = -1;
}
// 학교에서부터 출발하기에 1로 초기화
tileCase[n-1][m-1] = 1;
// 각 타일의 경우의 수 초기화
for(int i=n-1; i>=0; i--) {
for(int j=m-1; j>=0; j--) {
//웅덩이 타일일 경우
if(tileCase[i][j] == -1) {
tileCase[i][j] = 0;
}else{
// index out of bounds 방지
if(j != m-1) { // 오른쪽 타일 경우의 수 더하기
tileCase[i][j] += tileCase[i][j+1] % 1000000007;
}if(i != n-1) { // 아래 타일 경우의 수
tileCase[i][j] += tileCase[i+1][j] % 1000000007;
}
}
}
}
answer = tileCase[0][0] % 1000000007;
return answer;
}
}결과
채점 결과
정확성: 50.0
효율성: 50.0
합계: 100.0 / 100.0걸린시간
약 5분
마치며
큰 수를 다루는 문제를 처음 봐서 마지막에 실수가 있어서 이를 기억해야할 것 같다.
또한 무작정 수학적으로 생각하기보다 분할정복, 작은 문제로 나누는 방법을 우선으로 고려해봐야겠다.
총 걸린 시간
약 2시간 30분 정도 걸린 것 같다.
