출처 : 종만북 분할정복
선형 탐색과의 차이
단순한 연속된 자연수의 합을 생각해보자.
수열의 합 공식이 있지만 이를 사용하지 않고 재귀, 반복문을 통해 합을 구한다고 생각한다면
for(int i=1; i<=N; i++){
sum += i;
}
int func(int N){
if(N == 1)
return 1;
return func(N-1) + N;
}
다음과 같이 O(N)으로 구할 수 있다.
만약 이 과정을 절반으로 나누어서 구한다면 어떻게 될까?
1 + 2 + 3 + ~~~ + N은
(1 + 2 + 3 ~~ + N/2) + (N/2+1 +N/2 + 2 ~~ N/2+N/2)로 나타낼 수 있다.
(1 + 2 + 3 ~~ + N/2)를 식 X로 치환하고, 식을 조금 변환시킨다면
X + N/2 * N/2 + X = 2 * X + N/2 * N/2가 된다.
그러므로 1부터 N까지의 합은 2 * 절반의 합 + N/2 * N/2가 되며, 이 과정을 연속해서 수행한다면 O(NlogN)의 시간으로 재귀를 통한 연속된 수의 합을 구할 수 있다.
int fastSum(int N){
if(N == 1)
return 1; //base condition
if(N%2 == 1) // odd-case Inductive Step
return fastSum(N-1) + N;
// even-case Inductive Step
return 2 * fastSum(N/2) + (N/2) * (N/2)
}행렬의 N제곱을 두번째 예시로 들어보자.
행렬의 제곱은 O(N^3)의 시간복잡도로 계산할 수 있다. (N * N개의 원소에 대해 N번의 합)
이를 분할 정복을 통해서도 위의 예시와 비슷하게 나타낼 수 있다.
행렬의 N제곱은 N/2제곱 * N/2제곱과 같으므로, 이를 코드를 통해 나타낸다면
Matrix identityMatrix(int n); // return Identity Matrix to show m^0
int squareMatrix(Matrix m, int n){
if(n == 0) // base condition
return identityMatrix(m.size());
if(n%2 == 1)
return squareMatrix(Matrix m, n-1) * m;
return squareMatrix(Matrix m , n/2) * squareMatrix(Matrix m, n/2);
}이렇게 되면 행렬의 곱을 logN번 호출하게 되기 때문에 O(N^2logN)의 시간복잡도를 가지게 된다는 것을 알 수 있다.
홀수일 경우 절반으로 나누지 않는 이유?
위의 두 예시를 보면 경우의 수가 홀수일 경우에는 절반으로 나누지 않고 1을 빼 짝수를 만들어준 다음 절반으로 나누어주는 것을 확인할 수 있다.
이는 Overlapping-Subproblem 때문이다.
15를 예시로 들자.
홀수일 경우에도 절반으로 나누면
15
7 8
3 4 4 4
와 같이 트리 모양이 되고, 4가 중복되는 것을 확인할 수 있다.
결국 중복된 문제를 해결하는데 코스트가 더 들기 때문에, 1을 뺀 다음 짝수를 만드는 것이 더 효과적이라는 것을 알 수 있다.
Merge Sort
최적화된 정렬인 병합정렬도 분할정복을 이용한 정렬이다.
(입력은 정수 배열이라 가정)
Merge Sort
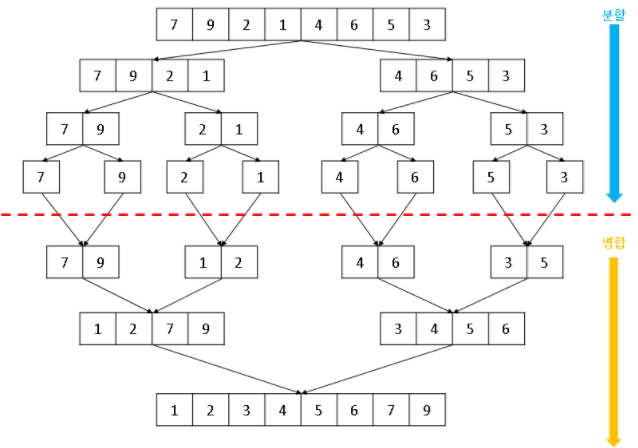
병합정렬은 다음과 같이 배열을 절반으로 나누고, base condition이 될때까지 나누다가 그 이후로 정렬을 하면서 병합하는 과정이다.
수리적 증명은 생략하고 단순하게 각각의 병합과정은 O(N), 병합 횟수는 O(logN)이므로 분할정복을 통한 O(NlogN)의 정렬 방식이다.
Quick Sort
병합정렬과 유사하지만 단순히 절반으로 나누는 것이 아닌 Pivot이라는 것을 만들어 이것을 기준으로 왼쪽, 오른쪽에 들어갈 원소들을 정한 후 분할하는 과정을 한다.
병합을 하지 않지만 Pivot을 기준으로 나누는데 O(N), 분할하는 횟수가 O(logN)이므로 O(NlogN)이지만 적합하지 않은 Pivot이 정해지는 경우 최악으로 O(N^2)가 걸릴 수 있다.
쿼드트리 뒤집기
https://algospot.com/judge/problem/read/QUADTREE#
#include <iostream>
using namespace std;
string func(string::iterator &iter){
char str = *(iter++);
if(str != 'x'){
return string(1, str);
}
string one = func(iter);
string two = func(iter);
string the = func(iter);
string four = func(iter);
return "x" + the + four + one + two;
}
int main(){
int T; cin>>T;
while(T--){
string s; cin>>s;
string::iterator iter = s.begin();
cout<<func(iter)<<'\n';
}
}전체를 뒤집는것은 사분면을 나눠서 뒤집는 과정과 동일하다. 그러므로 사분면으로 나누어 상하를 뒤집으면 된다.
*(iter++)
char c = *(iter++) 이라는 구문을 주의깊게 보자.
iterator에 후위연산자로 +를 할당하고, 이것의 포인터를 c에 집어넣었다.
그러면 후위연산자이기 때문에 c 에는 iter의 값이 들어가고, 그 이후에 iter += 1이 진행된다.
iterator를 이렇게 사용할 수 도 있다는 점을 항상 기억하자.
울타리 잘라내기
#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
using namespace std;
long long C, N, fence[100001];
long long sol(long long left, long long right){
if(left == right){
return fence[left];
}
long long mid = (left+right)/2;
long long ans = max(sol(left, mid), sol(mid+1, right));
long long midHeight = min(fence[mid], fence[mid+1]);
long long lo = mid, hi = mid+1;
ans = max(midHeight * 2, ans);
while(left < lo || hi < right){
if((hi < right) && (left == lo || fence[hi+1] > fence[lo-1])){
hi += 1;
midHeight = min(midHeight, fence[hi]);
}else{
lo -= 1;
midHeight = min(midHeight, fence[lo]);
}
ans = max(ans, midHeight * (hi-lo+1));
}
return ans;
}
int main(){
cin>>N;
for(long long i=0; i<N; i++)
cin>>fence[i];
cout<<sol(0, N-1)<<'\n';
}울타리의 너비가 정해지는 경우는 중간지점을 기준으로 세가지로 나누어진다.
1. 중간지점보다 왼쪽에서 정해지는 경우
2. 중간지점보다 오른쪽에서 정해지는 경우
3. 중간지점을 포함하는 경우
중간지점을 포함하는 경우, 중간의 왼쪽/오른쪽을 비교해나가면서 더 큰것을 선택하여 넓이를 구하면 된다.(귀류법 증명)
스위핑, 스택, disjoint set, Segment tree를 사용해서도 가능.
