오늘의 학습 목표는
🥕 다중 회귀에 대해 배우고 사이킷런의 여러 도구를 다뤄보기
🥕 복잡한 모델의 과대적합을 막기 위한 릿지와 라쏘 회귀를 배우기
입니다!
1. 다중 회귀
이전까지는 하나의 특성을 사용하여 선형 회귀 모델을 훈련시켰는데요, 여러 개의 특성을 사용한 선형 회귀를 다중회귀라고 합니다.
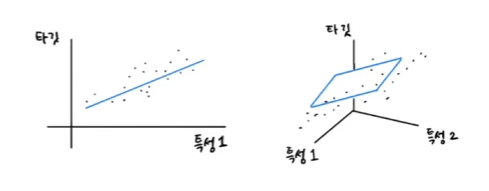
왼쪽 그림처럼 특성이 1개면 회귀모델은 직선을 학습합니다.
오른쪽 그림처럼 특성이 2개면 타깃값과 함께 3차원 공간을 형성하고 선형 회귀 방정식은
<타깃 = a x 특성1 + b x 특성2 + 절편>이 됩니다. 이때 모델은 평면을 학습하는 것을 확인할 수 있습니다.
그렇다면 특성이 3개 이상인 경우는 어떨까요? 이렇게 특성이 많은 고차원에서는 선형 회귀가 복잡한 모델을 표현할 수 있습니다.
특성 공학
- 기존의 특성을 사용해 새로운 특성을 뽑아내는 작업
예제에서 농어의 길이 뿐 아니라 농어의 높이와 두께도 함께 사용ㅎ겠습니다. 3개의 특성을 각각 제곱하여 추가하고, 각 특성을 곱해서 새로운 특성을 만들어 보겠습니다.
2. 데이터 준비
판다스
- 데이터 분석 라이브러리
데이터 프레임
- 판다스의 핵심 데이터 구조
- 넘파이 배열과 비슷하게 다차원 배열을 다룸
- 넘파이 배열로 쉽게 바꿀 수 있음
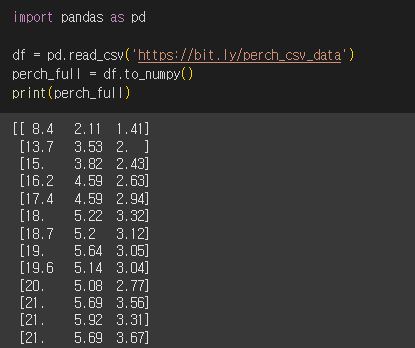
판다스를 사용해서 농어 데이터를 인터넷에서 내려받아 데이터 프레임에 저장합니다. 그 후 넘파이 배열로 변환하여 선형 회귀 모델을 훈련해보겠습니다.
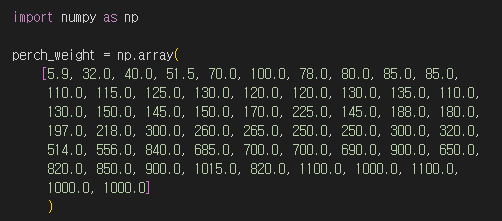
타깃 데이터는 이전과 동일한 방식으로 준비합니다.
훈련세트와 테스트 세트를 나눠 데이터셋 준비가 끝났습니다.

3. 사이킷런의 변환기
변환기
- 사이킷런에서 특성을 만들거나 전처리하기 위한 클래스
- 모델 클래스: fit( ), scroe( ), predict( )
- 변환기 클래스: fit( ), transform( )
PolynomialFeatures( )
- 각 특성을 제곱한 항을 추가하고 특성끼리 곱한 항을 추가
PolynomialFeartures 클래스를 사용하는 연습을 해보겠습니다.
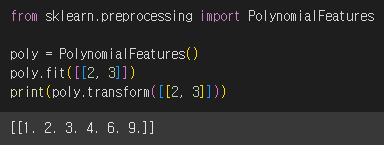
2와 3으로 구성된 특성이 2개인 샘플 데이터에 적용을 해보았습니다. fit( ) 매서드는 새롭게 만들 특성 조합을 찾고 transform( ) 매서드는 실제로 데이터를 변환합니다.
PolynomialFeatures 클래스는 각 특성을 제곱한 항을 추가하기 때문에 4와 9가 추가되었고 특성끼리 곱한 값이 추가되기 때문에 2 x 3 인 6이 추가되었습니다.
그렇다면 1은 왜 추가가 되었을까요?
무게 = a x 길이 + b x 높이 + c x 두께 + d x 1
선형 방정식의 절편을 항상 값이 1인 특성과 곱해지는 계수라고 볼 수 있기 때문에 특성은 (길이, 높이, 두께, 1)이 됩니다.
하지만 사이킷런의 선형 모델은 자동으로 절편을 추가하므로 굳이 이렇게 특성을 만들 필요가 없으므로 include_bias=False로 지정해서 변환합니다.
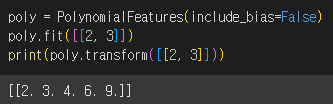
include_bias=False 로 지정하지 않아도 사이킷런 모델은 자동으로 추가된 절편 항을 무시
이제 train_input을 변환해보겠습니다.
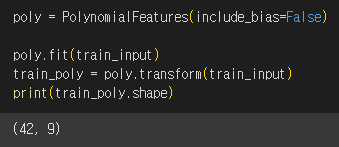
PolynomialFeatures 클래스는 각 특성이 어떻게 만들어졌는지를 확인하는 get_feature_names_out( ) 이라는 매서드를 제공합니다.

테스트 세트까지 변환한 후 변환된 특성을 사용해서 다중 회귀 모델을 훈련하겠습니다.

4. 다중 회귀 모델 훈련하기
다중 회귀 모델은 선형회귀 모델을 훈련하는 것과 같습니다.다만 여러개의 특성을 사용한다는 점에서 차이가 있죠.
LinearRegression 클래스를 사용해서 학습합니다.
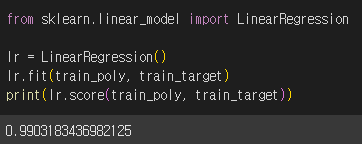
아주 높은 점수가 나왔습니다! 이번에는 테스트 점수도 확인해보겠습니다.

테스트 세트에 대한 점수는 높아지지 않았지만 농어의 길이만 사용했을 때 있던 과소 적합 문제가 해결되었습니다 :)
특성을 더 많이 추가해보면 어떨까요? 3제곱, 4제곱 항을 넣어보겠습니다.
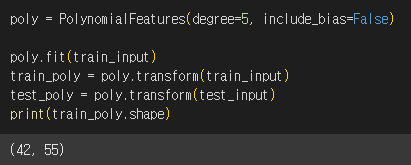
degree 매개변수
- PolynomialFeatures 클래스에서 필요한 고차항의 최대 차수 지정
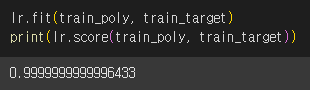
고차항 데이터를 학습했더니 아주 높은 점수가 나왔습니다.
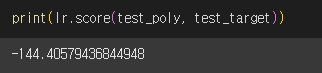
하지만 테스트 점수가 음수가 나왔습니다..?
특성의 개수를 크게 늘리면 선형 모델은 훈련 데이터에 대해 거의 완벽하게 학습할 수 있습니다. 하지만 이런 모델은 훈련 세트에 너무 과대적합되는 문제가 있습니다.
이번에는 과대 적합을 줄이는 방법을 알아보겠습니다.
5. 규제
규제
- 머신러닝 모델이 훈련 세트를 너무 과도하게 학습하지 못하도록 방해하는 것
- 선형회귀 모델의 경우 특성에 곱해지는 계수(기울기)의 크기를 작게 만드는 일
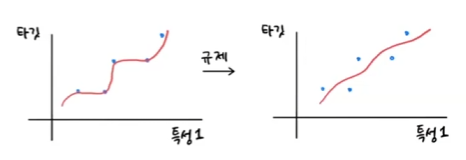
왼쪽 그래프는 훈련 세트를 과도하게 학습했고, 오른쪽 그래프는 기울기를 줄여 보편적인 패턴을 학습합니다.
선형 회귀 모델의 계수를 규제하여 훈련 세트의 점수를 낮추고 테스트 세트의 점수를 높여보겠습니다.
정규화
규제를 적용하기에 앞서 특성의 스케일을 정규화해줘야 합니다. 왜냐하면 규제를 적용할 때 계수 값의 크기가 서로 많이 다르면 공정하게 제어되지 않기 때문입니다.
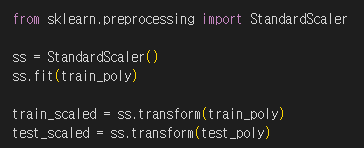
StabdardScaler 클래스의 객체를 초기화 한 후 train_poly를 사용해 객체를 훈련합니다. 그리고 훈련 세트로 학습한 변환기를 사용해서 테스트 세트까지 변환합니다.
릿지
- 선형회귀 모델에 규제를 추가한 모델로 계수를 제곱한 값을 기준으로 규제 적용
라쏘
- 선형회귀 모델에 규제를 추가한 모델로 계수의 절댓값을 기준으로 규제를 적용
6. 릿지 회귀
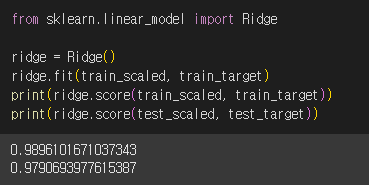
사이킷런에서 릿지 회귀 모델을 호출해서 학습을 완료했습니다. 규제를 적용하니 선형회귀에서 거의 완벽에 가까웠던 점수가 조금 낮아졌습니다. 테스트 세트 점수가 정상으로 돌아온 것도 보입니다!
많은 특성을 사용했음에도 불구하고 훈련세트에 과대 적합되지 않았네요 👍🏻
alph
- 규제의 강도를 조절하는 하이퍼파라미터
- 값이 커지면 규제 강도가 세져, 계수 값을 줄이고 과소적합되도록 유도한다.
적절한 alpha 값을 찾는 방법은 alpha 값에 대한 값의 그래프를 그려보는 것 입니다.
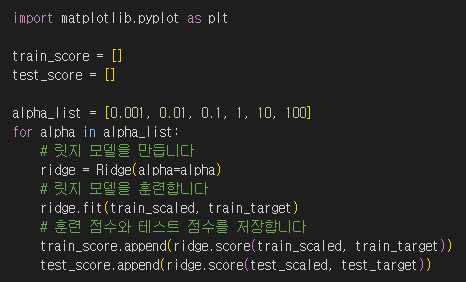
alpha 값을 0.001에서 100까지 10배씩 늘려가며 릿지 회귀 모델을 훈련한 다음 훈련 점수와 테스트 점수를 저장했습니다.
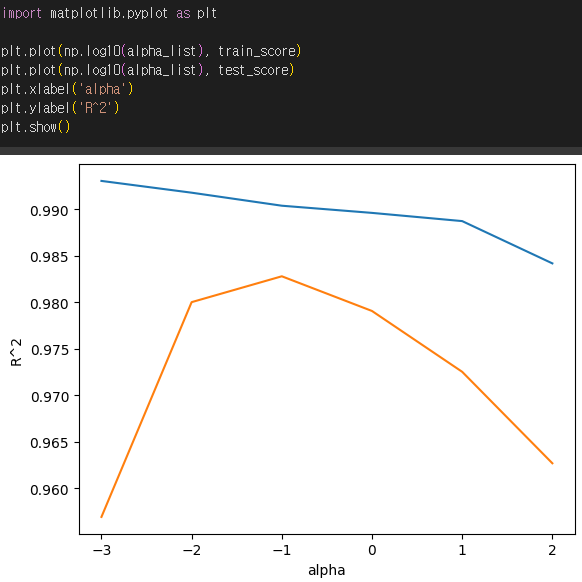
alpha 값을 0.01부터 10배씩 늘렸기 때문에 그래프 왼쪽이 너무 촘촘해지는 것을 방지하기 위해 alpha_list의 값을 로그함수로 바꾸어 지수로 표현해줬습니다.
np.log( )
- 자연 상수 e를 밑으로 하는 자연로그
np.log10( )
- 10을 밑으로 하는 상용로그
파란선이 훈련세트 그래프, 주황선이 테스트 세트 그래프입니다.
적절한 alpha 값은 두 그래프가 가장 가깝고 테스트 점수가 가장 높음 -1, 즉 입니다.
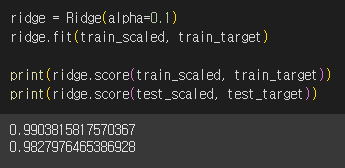
alpha를 0.1로 해서 릿지 회귀 모델을 다시 학습 했습니다.
훈련 세트와 테스트 세트의 점수가 비슷하게 모두 높고 과대 적합과 과소 적합 사이의 균형을 맞추고 있습니다~~🙌🏻
7. 라쏘 회귀
Ridge 클래스를 Lasso 클래스로 변경해서 라쏘 회귀 모델도 학습해보겠습니다.
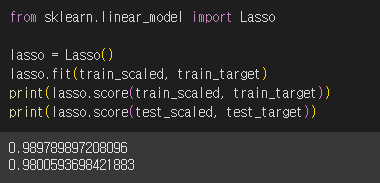
마찬가지로 과대적합을 잘 억제한 결과를 확인할 수 있습니다.
alpha 값을 바꾸어 점수를 계산해보겠습니다.

train_score와 test_score를 사용해 그래프를 그려보겠습니다.
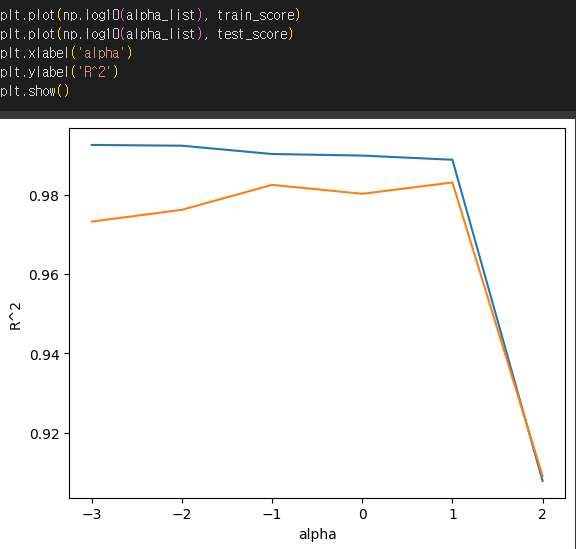
왼쪽은 과대 적합을, 가장 오른쪽은 과소적합을 보여줍니다.
최적의 alpha 값은 1즉 $10^1$10입니다.
coef_
- 라쏘 모델의 계수가 저장되어있음
라쏘 모델은 릿지 모델과 달리 계수 값을 아예 0으로 만들 수 있습니다. 계수가 0인 경우를 확인해보겠습니다.
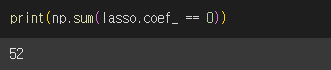
np.sum( )
- 배열을 모두 더한 값 반환
- 넘파이 배열에 비교 연산자를 사용하면 각 원소는 True 혹은 False가 됨
- np.sum( ) 함수는 True를 1로 False를 0으로 인식하여 덧셈 수행
52 개나 계수가 0이라는 것은 55개 특성 중 3개만 사용되었다는 뜻입니다. 이런 특징 때문에 라쏘 모델을 유용한 특성을 골라내는 용도로도 사용할 수 있습니다.
여기까지 특성공학과 규제에 대해서 공부해보았습니다. 다음 장에서는 로지스틱 회귀에 대해서 다뤄보겠습니다~!
자료출처: 한빛미디어
