⚠️ 이 글은 경북대학교 컴퓨터학부 이시형 교수님의 '알고리즘2' 수업을 수강하고 배운 점들을 복습하며 기록한 글입니다. 본문 내용을 비롯하여 사진 자료와 코드 또한 이시형 교수님의 수업자료에서 발췌하였습니다. 또한 모든 코드는 python을 사용합니다.
프로그래밍 언어의 정렬 기능은 주로 Merge sort와 Quick sort를 기반으로 동작한다. 이 두 정렬 방법은 거의 항상 좋은 성능이 보장됨이 보여진 바 있다.
Merge Sort
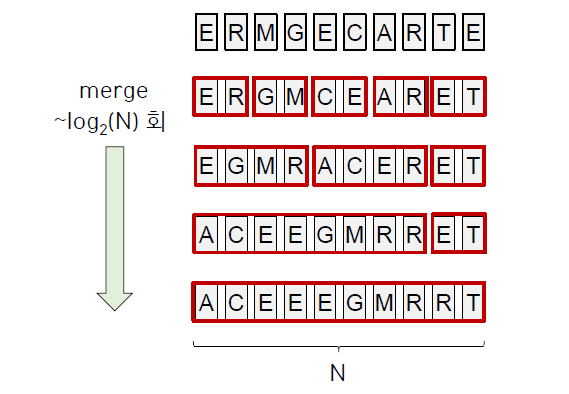
인접한 두 조각끼리 Merge 하는 것을 반복
각 조각들을 순서에 맞게 차례로 결과 배열에 옮겨 담는다. 이 과정은 1번의 선형 탐색이 이루어지고 (~N) 이러한 작업이 logN번 반복된다.
또한 입력 데이터의 크기가 N이라면 결과를 옮겨 담을 ~N의 추가 공간 할당이 필요하다.
Merge Sort의 기본 코드
def mergeSort(a):
random.shuffle(a)
aux = [None] * len(a)
# aux라는 배열에 정렬 결과를 담을 것
# 3, 4번째 인자로 정렬을 수행할 배열의 처음과 끝 인덱스를 지정해 줌
divideNMerge(a, aux, 0, len(a)-1)
def divideNMerge(a, aux, lo, hi):
# 만약 lo가 hi와 같다면 길이가 1인 배열이므로 a 그 자체를 리턴
if hi <= lo:
return a
# lo와 hi의 중간 지점인 mid 변수를 선언
mid = (lo + hi) // 2
# 중간 지점을 기준으로 두 배열 (처음~중간), (중간+1~끝)을 각각 정렬할 수 있도록 본 함수를 재귀 호출한다.
divideNMerge(a, aux, lo, mid)
divideNMerge(a, aux, mid+1, hi)
# (처음~중간), (중간+1~끝) 배열을 하나로 합친다.
merge(a, aux, lo, mid, hi)
# 배열 a 내에 lo~mid, mid+1~hi 두 범위로 각각 정렬이 되어 있는 상태.
# 이 a 배열을 aux에 그대로 옮겼다가 정렬 순서에 맞게 재배열 할 것임
def merge(a, aux, lo, mid, hi):
for i in range(lo, hi+1):
aux[i] = a[i]
i, j = lo, mid + 1
for k in range(lo, hi+1):
if i > mid:
a[k], j = aux[j], j+1
elif j > hi:
a[k], i = aux[i], i+1
elif aux[i] <= aux[j]:
a[k], i = aux[i], i+1
else:
a[k], j = aux[j], j+1Merge Sort의 성능
인접한 두 조각끼리를 merge 하는 데에 전체 배열을 탐색하므로 ~N 시간이 소요되고, 전체 배열 크기 N을 더는 쪼갤 수 없을 때까지 쪼개는 횟수만큼(logN)번 반복하게 된다.
즉 merge sort의 시간 복잡도는 NlogN 이며, 이는 입력 데이터가 달라지더라도 크게 변하지 않는다. 예를 들어 이미 정렬된 상태의 데이터가 들어오더라도 여전히 NlogN 회의 비교 및 옮겨 담는 작업을 수행한다.
Merge Sort의 단점
merge sort는 배열을 재귀 호출을 거듭하며 절반씩 쪼갠 후 이를 반환하며 병합 및 정렬하는 순서로 동작한다. 이 때 배열을 나누어 가는 과정에서 재귀 호출이 계속되며 시간적, 공간적인 overhead가 커지게 된다.
또한 함수 호출 및 반환 과정에서 함수의 인자나 변수들을 메모리에 저장하고 삭제하기를 반복해야 한다는 단점이 있다.
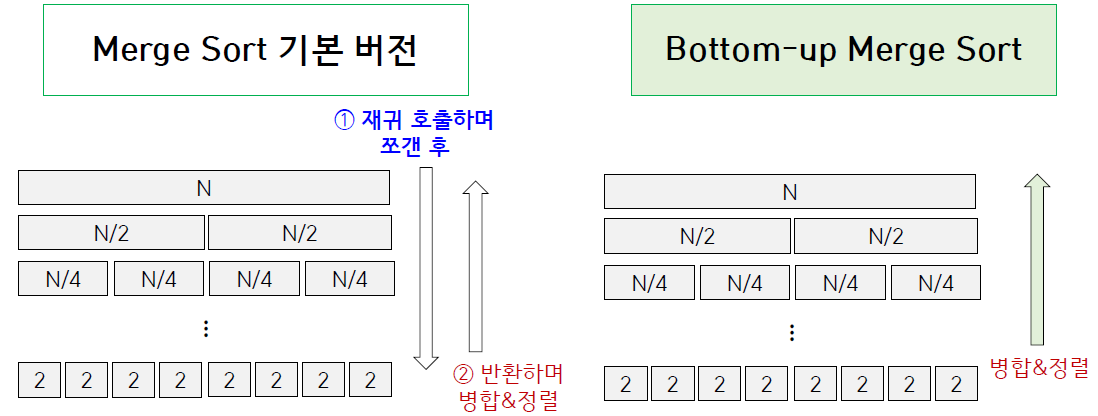
Bottom-up merge sort
재귀 호출 하는 과정을 생략하여, 작은 부분 배열에서부터 병합(merge)을 해 나가는 방법
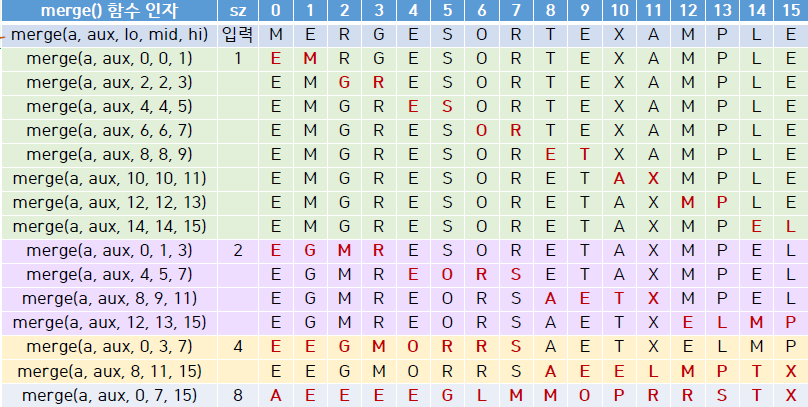
sz= 1에서 시작- 크기가
sz인 인접한 부분집합끼리 병합 sz크기를 2배 하고,sz >= N될 때까지 반복
코드
def mergeSort(a):
aux = [None] * len(a)
sz = 1
while (sz < len(a)):
for lo in range(0, len(a)-sz, sz * 2):
merge(a, aux, lo, lo+sz-1, min(len(a)-1, lo+sz+sz-1))
sz *= 2
# merge 함수는 동일하게 사용
def merge(a, aux, lo, mid, hi):
for i in range(lo, hi+1):
aux[i] = a[i]
i, j = lo, mid + 1
for k in range(lo, hi+1):
if i > mid:
a[k], j = aux[j], j+1
elif j > hi:
a[k], i = aux[i], i+1
elif aux[i] <= aux[j]:
a[k], i = aux[i], i+1
else:
a[k], j = aux[j], j+1
merge 함수 마지막 인자에
min()함수 사용한 이유?
-> 두 번째 조각의 크기가 sz보다 작아질 수 있다. 그래서lo+sz-1+sz하게 된다면out of range오류가 발생할 수 있다.
Quick Sort
정렬할 원소 하나를 기준값
v로 정한 후 v보다 작거나 같은 원소는 v 왼쪽에, v보다 크거나 같은 원소는 v 오른쪽에 두는 분할(partition) 을 반복하는 방법
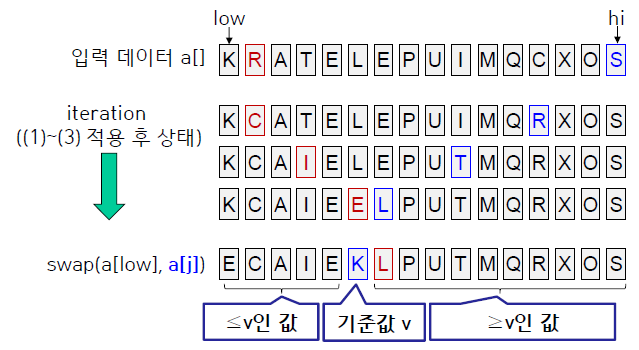
quick sort는 다음과 같이 동작한다.
- 정렬해야 하는 배열의 첫 원소를 기준값
v로 정한다. (다른 방식으로 기준값을 잡아도 상관 X) - 기준값을 제외한 나머지 배열의 양 끝에 포인터를 하나씩 둔다. (편의상
i,j라고 가정) i가j를 지나쳐갈 때까지, 즉i >= j일 때까지 다음을 반복
-v보다 큰a[i]가 나올 때까지i를 1씩 증가시키면서 탐색v보다 작은a[j]가 나올 때까지j를 1씩 감소시키면서 탐색a[i]와a[j]를 서로 맞바꿈(swap)
- 두 포인터가 서로 교차하였을 때 두 partition의 경계에 있는 값과
v를 swap (그 위치가v의 올바른 위치) v좌우의 배열에 대해 재귀적으로 quick sort 반복하여 수행

이 과정을 수행하였을 때 배열의 크기가 2인 배열을 quick sort 하면 정렬이 완료된다.
Stability of Sorting
stability of sorting(정렬의 안전성) 이란, 정렬 전 후 같은 원소 간 상대 순서를 보존하는 성질을 말한다.
정렬의 안전성은 주로 한 번 정렬을 수행한 후, 다른 기준에 대해 재차 정렬을 수행했을 때 고려한다.
예를 들어, 학생의 이름, 학년, 전화번호 등 개인정보가 담긴 테이블이 있다고 가정하고, 먼저 이름을 사전순으로 정렬하였다고 생각해 보자.
이후 학년을 오름차순으로 정렬한다고 했을 때, stable한 정렬의 경우 이름의 사전순 배열이 유지된 채로 학년 순으로 정렬된다. 그러나 unstable한 정렬의 경우 이름으로 정렬한 결과가 뒤죽박죽 섞이게 된다.
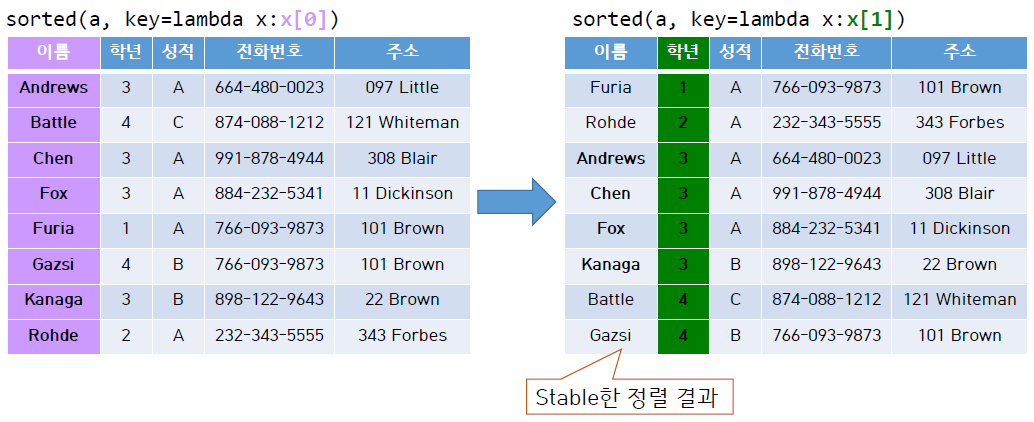
위의 표를 보면 학년 순으로 재차 정렬을 하였을 때, 같은 학년에 대해 이름순 정렬이 깨지지 않고 유지되어 있는 모습을 볼 수 있다.
즉 위의 정렬은 stable한 정렬이다.
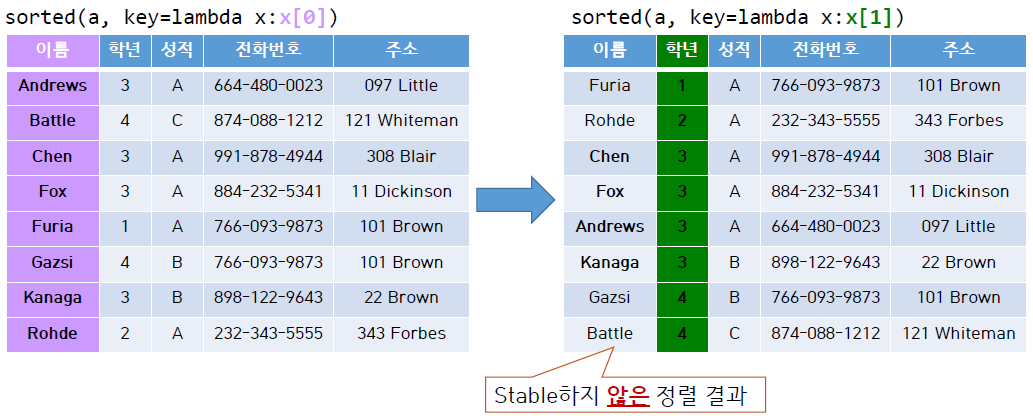
그러나 위의 표를 보면 학년 순 정렬을 했을 때 이름 정렬이 깨지게 되었다.
즉 위의 정렬은 unstable하다고 할 수 있다.
각 정렬의 stability
insertion sort
insertion sort를 다시 살펴보면, iteration i 에 a[i]를 a[0] ~ a[i-1] 중에 적절한 위치에 삽입하는 과정을 거친다.
def insertionSort(a):
for i in range(1, len(a)):
key = a[i]
j = i - 1
while j >= 0 and a[j] > key:
a[j+1] = a[j]
j -= 1
a[j+1] = key그리고 적절한 위치 란, a[i]보다 작은 수를 만날 때까지 왼쪽으로 이동함을 반복하면서 찾는다.
즉 자기와 같은 수가 만나면 좌로 이동하기를 그만두기 때문에, 자기와 같은 수를 건너뛰어 갈 수 없다. 그러므로 stable한 정렬이 가능하다.
즉 insertion sort의 경우 stable sort 이라고 할 수 있다.
selection sort
selection sort는 iteration i에 a[i] ~ a[n-1] 중 최솟값을 찾아 a[i]와 swap 하는 과정을 거친다.
def selectionSort(a):
for i in range(len(a)-1):
min_idx = i
for j in range(i+1, len(a)):
if a[j] < a[min_idx]:
min_idx = j
# swap the found minimum with a[i]
a[i], a[min_idx] = a[min_idx], a[i]이 때는 a[i]에 위치하고 있는 값이 a[min_idx]와 swap 되면서 a[i]와 같은 값을 가진 다른 원소를 넘어갈 수가 있다.
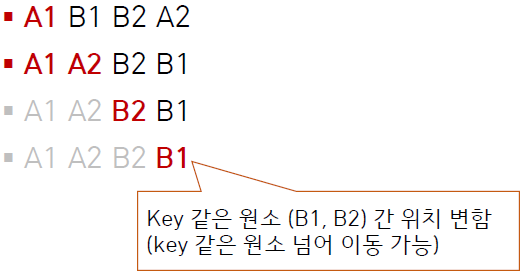
B1이 B2보다 앞에 있었는데 정렬을 완료한 결과 뒤로 간 것을 볼 수 있다.
즉 selection sort는 unstable하다.
merge sort
merge sort는 앞서 다루었듯 배열을 보다 작은 조각으로 나누고, 인접한 조각끼리 merge하기를 반복한다.
def merge(a, aux, lo, mid, hi):
for k in range(lo, hi+1):
aux[k] = a[k]
i, j = lo, mid+1
for k in range(lo, hi+1):
if i > mid:
a[k], j = aux[j], j+1
elif j > hi:
a[k], i = aux[i], i+1
elif aux[i] <= aux[j]:
a[k], i = aux[i], i+1 # 이 부분에 주목
else:
a[k], j = aux[j], j+1주석 처리한 곳을 잘 보면 aux[i]와 aux[j]가 같을 때 앞의 배열, 즉 i의 값을 선택함을 볼 수 있다.
정리하면 a[k]에 aux[i]를 넣는 조건에 등호를 추가함으로써 같은 값이 있을 때 왼쪽의 값을 먼저 선택, stability를 지킬 수 있다.
quick sort
def partition(a, lo, hi):
i, j = lo+1, hi
while True:
while j <= hi and a[i] < a[lo]:
i += 1
while j >= lo+1 and a[j] > a[lo]:
j -= 1
if j <= i:
break
a[i], a[j] = a[j], a[i]
i, j = i+1, j-1
a[lo], a[j] = a[j], a[lo]
return jquick sort도 selection sort와 마찬가지로 정렬 과정 중에 swap하는 과정이 있으므로 unstable하다.
정리
stability는 정렬에서 매우 중요한 요소이다.
우리의 일상 생활에서도 stable한 정렬이 주는 편리함이 많다. 노래 플레이리스트에서 가수이름순으로 정렬했다가 날짜순으로 정렬한다거나, 또는 비행기 시간표에서 목적지 이름순으로 정렬했다가 출발 시간순으로 정렬한다거나, 여러 개의 정렬 조건을 거는 경우가 많기 때문이다.
그런 맥락에서 merge sort는 stable할 뿐만 아니라 worst case에서도 NlogN의 시간 복잡도를 가지므로, 일부 어플리케이션에서는 quick sort보다 선호된다.
select
어떤 배열
arr이 있고, 그 배열에서k번째로 작은 수를 찾고자 한다고 하면, 어떤 방식이 효과적일까?
가장 먼저 생각나는 방법은 당연히 NlogN만에 정렬을 수행한 뒤 a[k-1]를 찾는 방법일 것이다. 이것보다 효율적일 수는 없을까?
k가 0에 가까워서 거의 최솟값에 근접한 숫자이거나 n-1에 가까워서 거의 최댓값에 근접한 숫자일 때 더 빠르게 수행할 수 있는 방법이 있을까?
quick select
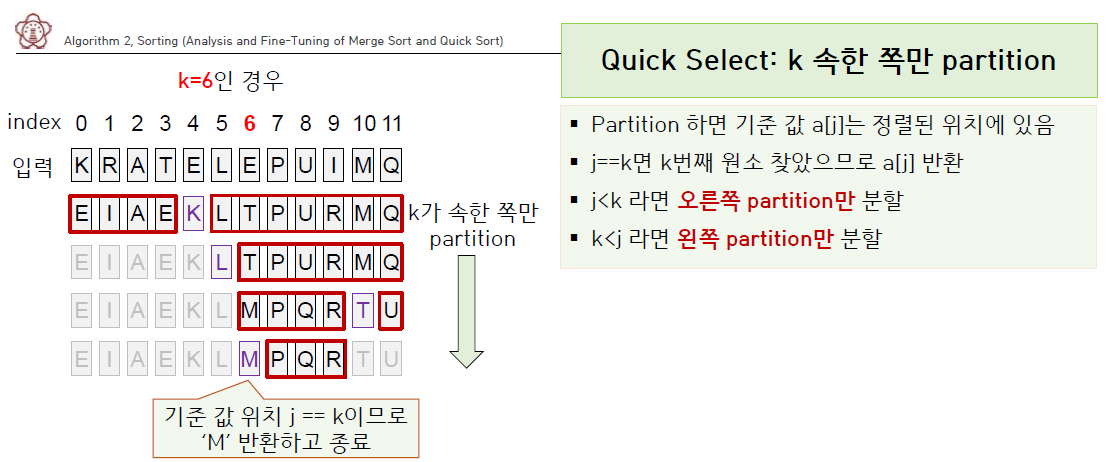
quick sort는 어느 특정 값을 기준으로 작은 값은 왼쪽, 큰 값은 오른쪽에 위치하게 되며 이 좌우 조각 모두에 다시 partition을 적용한다.
여기서 k가 속한 쪽만 partition을 수행함으로써 시간을 절약할 수 있다.
def quickSelect(a, k):
lo, hi = 0, len(a)-1
while lo < hi:
j = partition(a, lo, hi)
if j < k:
lo = j + 1
elif j > k:
hi = j - 1
else:
return a[k]
return a[k]while문 안의 조건을 살펴보면, j<k일 경우 찾는 값이 j보다 크므로 오른쪽 조각에 대해서 다시 partition을 수행한다.
j>k일 경우 찾는 값이 j보다 작으므로 왼쪽 조각에 대해서만 다시 partition을 수행한다.
j==k일 경우 찾는 값이 j이므로 바로 리턴할 수 있다.
한 조각에 대해서만 partition을 이어서 수행하므로 partition의 크기가 대략 반으로 나누어간다면 N + N/2 + N/4 + N/8 ... = 2N 횟수의 비교를 거친다.
그런데, N개 원소를 partition했을 때 결과가 N-1개가 나오는 경우가 존재할 수 있고 이것이 worst case이다.
이 경우에는 N + (N-1) + (N-2) ... = N^2/2에 비례한 횟수의 비교를 거친다.
평균적으로 2N, N에 비례한 횟수의 비교를 통해 k번째 작은 값을 찾을 수 있으므로 전체 배열을 sort하는 것보다는 효과적이라 할 수 있을 것이다.
3-way partition quick sort
중복값 duplicate key 이 많은 경우에 quick sort의 정렬 속도를 개선할 수 있다.
지금까지 배운 quick sort의 매커니즘은 2-way partition 이었다. 기준 값 v를 찾고, 그 기준 값 v를 기준으로 좌 우 조각에 다시 partition을 적용한다.
이 챕터에서 살펴볼 방법은 3-way partition으로, 기준 값인 원소, 기준 값보다 작은 원소, 기준 값보다 큰 원소 3개의 partition으로 나누는 것이다. 그리고 기준 값인 원소를 제외한 2개의 조각에 다시 partition을 적용한다.
구현
a[lo ~ hi] 중에서 a[lo]를 기준값 v로 정한다.
최종적으로 3개의 영역으로 나누고자 한다.
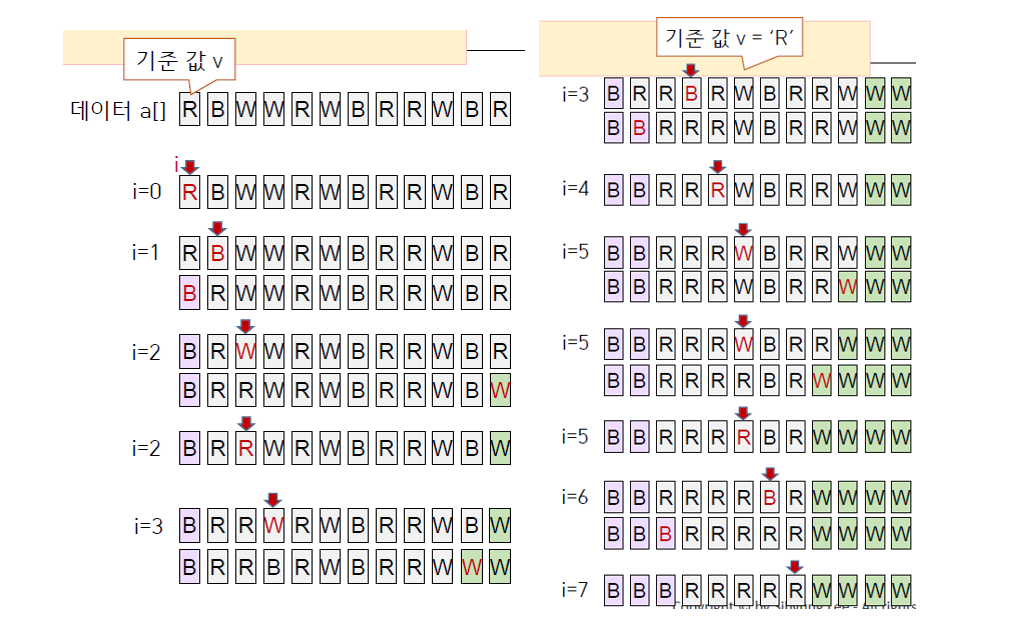
한 번에 한 원소 a[i]를 검사하여, 다음과 같은 조건에 의해 3가지 영역으로 나눈다.
a[i] < v이면 왼쪽 영역의 오른쪽 끝으로 이동.i++a[i] == v이면 이동시키지 않음.i++a[i] > v이면 오른쪽 영역의 왼쪽 끝으로 이동i가 오른쪽 영역에 들어서면 검사를 중단
def partition3Way(a, lo, hi):
if hi <= lo: return
lt, gt = lo, hi
i = lo
v = a[lo]
while i <= gt:
if a[i] < v:
a[i], a[lt] = a[lt], a[i]
i += 1
lt += 1
elif a[i] > v:
a[i], a[gt] = a[gt], a[i]
gt -= 1
else:
i += 1
# print(a)
# v값보다 작은 구역에서 다시 3-way partitioning을 진행
partition3Way(a, lo, lt-1)
# v값보다 큰 구역에서 다시 3-way partitioning을 진행
partition3Way(a, gt+1, hi)정리
| - | merge sort | quick sort | 3-way quick sort |
|---|---|---|---|
| 방법 | 작은 조각 -> 큰 조각 순으로 merge | 큰 조각 -> 작은 조각 순으로 partition | 3조각으로 분할 |
| best case | NlogN | NlogN | N |
| average case | NlogN | NlogN | NlogN |
| worst case | NlogN | N^2/2 | N^2/2 |
| stability | Yes | No | No |