위의 글에 이어 제 3, 그리고 보이스코드 정규형에 대해 알아봅니다.
앞서, 모든 도메인이 원자 값으로 이루어진 릴레이션을 제 1정규형이라 하였고, 제 1정규형의 문제점인 부분 함수 종속을 해결한 것이 제 2정규형이라고 하였다.
그리고 제 2정규형의 이행적 함수 종속을 해결한 것이 제 3정규형이다.
제 3정규형
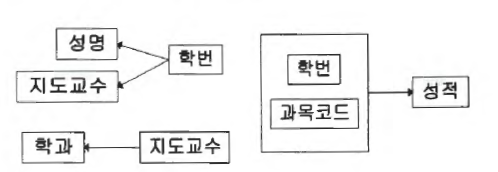
이행적 함수 종속을 제거하여 3개의 릴레이션을 만들었고, 이제 각 릴레이션마다 함수의 종속이 연결되는 일이 없어졌다.
일반적으로 데이터베이스에서 3NF는 거의 완벽한 수준이라고 말할 수 있고 데이터베이스 설계의 목표가 3NF를 만드는 것이라 할 수 있다.
그러나 간혹 3NF이지만 문제점이 있는 예가 있다. 만약 아래와 같은 릴레이션이 있다고 하자.
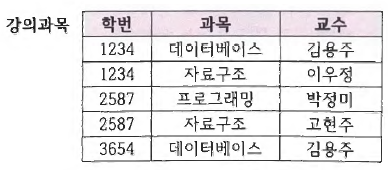
그리고 현실적으로는 거의 불가능한 경우이지만 이에 대한 제약 조건이 다음과 같다고 가정해 보자.
- 한 학생은 여러 과목을 수강할 수 있다.
- 한 교수는 한 과목만 강의할 수 있다.
- 한 과목은 여러 교수가 강의할 수 있다.
그리고 함수 종속 관계는 다음과 같다.
- {학번, 과목} -> 교수
- 교수 -> 과목
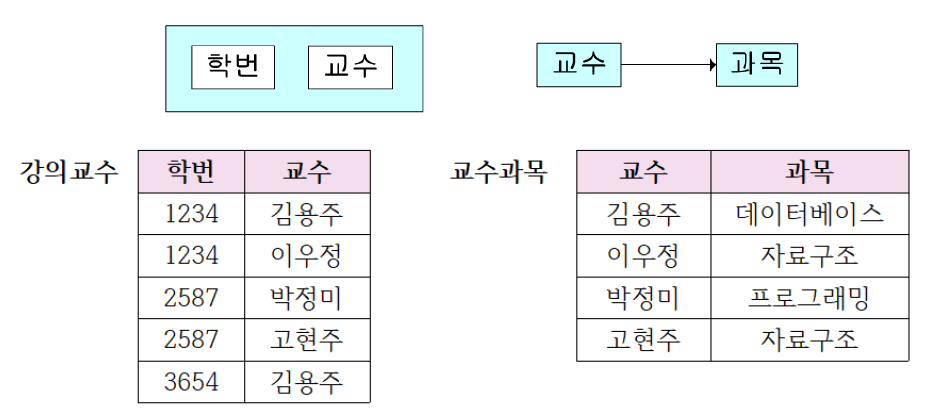
이를 바탕으로 FD Diagram을 그려보면 다음과 같을 것이다.
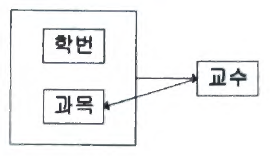
여기서 {학번, 과목}과 교수의 관계는 문제가 없어 보이지만 교수와 과목의 관계에서 관계가 조금 불안정한 점이 있다.
제 3정규형의 anomaly
삽입 이상
'홍길동' 교수가 '자료구조' 과목을 강의하게 되었을 때 기본키인 학번이 NULL 이므로 삽입이 불가능하다.
삭제 이상
학번이 '1234'인 학생이 '자료구조' 수업 수강을 취소할 때 '이용주' 교수가 '자료구조' 수업을 맡고 있다는 정보도 삭제된다.
갱신 이상
교수 '김용주' 의 강의과목이 '데이터베이스' 에서 '웹프로그래밍'으로 변경 되었을 때 '김용주'에 대한 모든 튜플에 대해 변경되어야 한다. 그렇지 않다면 일관성에 문제가 생긴다.
조금 억지스러울 수 있지만 어쨌든 제 3정규형이라 할지라도 anomaly가 발생할 수 있다.
이러한 현상이 나타나는 이유는 릴레이션에서 키가 아닌 속성이 다른 속성을 결정하기 때문 이다. 즉 기본키인 {학번, 과목} 이 아니라 교수 역시 과목을 특정할 수 있다. 즉 교수 속성은 결정자이다.
이러한 문제점을 해결한 것이 바로 보이스(Boyce)와 코드(Codd)가 만든 보이스 코드 정규형이다. 제 3정규형으로도 해결되지 않은 중복 문제점을 해결하기 때문에 제 3.5정규형이라고도 한다.
보이스-코드 정규형 (BCNF)
제 3정규형에서
모든 결정자가 후보키가 되도록분할한 것을 말한다.
후보키는 최소성과 유일성을 만족해야 한다. 즉 후보키만으로 릴레이션에서 튜플을 특정할 수 있는 능력이 있어야 하며, 유일성을 가지는 데 꼭 필요한 속성들만으로 구성되어야 한다.
위의 3NF에서 다룬 릴레이션을 다시 가져오면,

각 교수는 한 과목만 맡을 수 있으므로 과목 속성에 대해 결정자 라고 할 수 있다.
그렇지만 '김용주', '고현주' 등의 교수 정보만 가지고는 튜플을 식별할 수 없다. 즉 후보키가 될 수 없다.
즉 교수 속성 역시 후보키가 될 수 있게끔 릴레이션을 분할하면 다음과 같다.
제 4정규형 (4NF)
다음과 같은 제약조건이 있는 비정규형 테이블이 있다.
- 각 과목은 명시된 교수들 중에서는 누구나 강의할 수 있다.
- 교재는 명시된 것 전부 사용해야 한다.
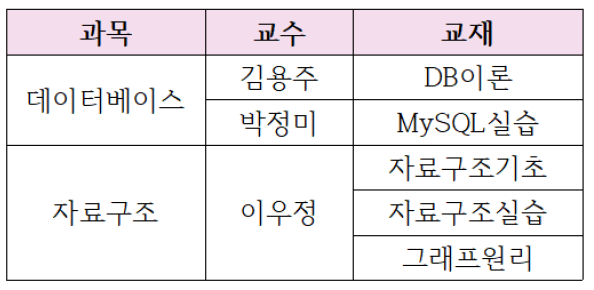
모든 도메인을 원자값으로 표현한 제 1정규형 릴레이션으로 표현하면 다음과 같을 것이다.
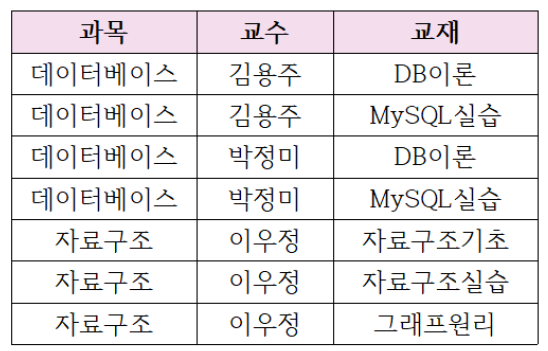
이 릴레이션의 키는 모든 속성인 {과목, 교수, 교재} 이다. 즉 모든 결정자가 후보키이므로 BCNF이다.
그러나 이 릴레이션은 사실상 무관하다고 볼 수 있는 교수, 교재를 한 릴레이션으로 표현하고 있다.
위의 릴레이션에서는 과목이 하나 정해지면 (교수, 교재)가 하나씩만 결정되는 것이 아니라, 여러 개의 (교수, 교재)가 결정될 수 있다. 종속이 되지 않는건 아니지만 함수처럼 일대일 매칭은 아니라는 뜻. 이러한 형태의 종속을 다치 종속 (MVD : Multi-Valued Dependancy) 이라고 한다. 다르게 말하면 과목은 교수와 교재를 다치 결정한다 라고 할 수 있다.
이를 표시할 땐 연속된 화살표(->>)로 나타낸다. 즉 위 릴레이션은 다음과 같은 두 개의 종속 관계를 가진다.
- 과목 ->> 교수
- 과목 ->> 교재
그리고 이러한 다치 종속은 항상 쌍으로 나타난다. 그래서 과목 ->> 교수|교재 로 한 번에 표시할 수 있다.
한 릴레이션에 다치 종속이 존재하지 않게끔 한 릴레이션이
제 4정규형(4NF)이다.
과목으로부터 다치 종속되는 두 개의 속성인 교수와 교재를 서로 분리하여 두 개의 릴레이션으로 만든 4NF 릴레이션은 다음과 같다.
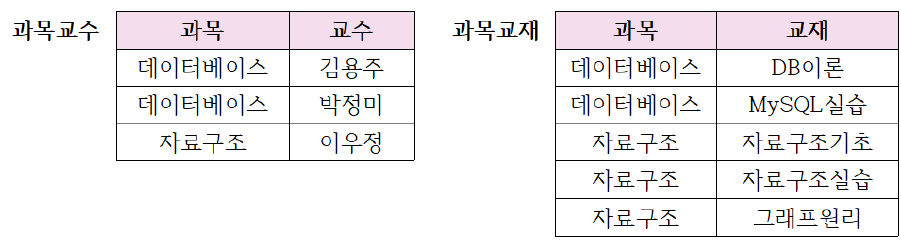
과목교수 릴레이션의 키는 {과목, 교수} 이고 과목교재 릴레이션의 키는 {과목, 교재} 이다.
제 5정규형 (5NF)
지금까지 문제가 발생한 릴레이션을 두 개로 쪼개어 각각의 문제를 해결해 왔다. 그러나 3개 또는 그 이상의 릴레이션으로 분해해야 하는 경우도 있을 수 있다.
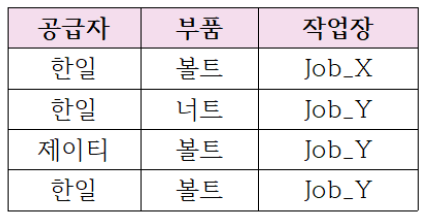
위의 납품관리 릴레이션은 어떤 공급자 회사가 어떤 부품을 어떤 작업장에 납품하고 있는지를 보여준다. 이 릴레이션은 다치 종속도 존재하지 않으며 모든 속성의 집합이 키가 되므로 이미 4NF에 속한다. 따라서 현실적으로 큰 문제는 되지 않지만 이를 속성들의 부분집합으로 쪼개서 3개의 릴레이션을 만들어 보면 다음과 같다.
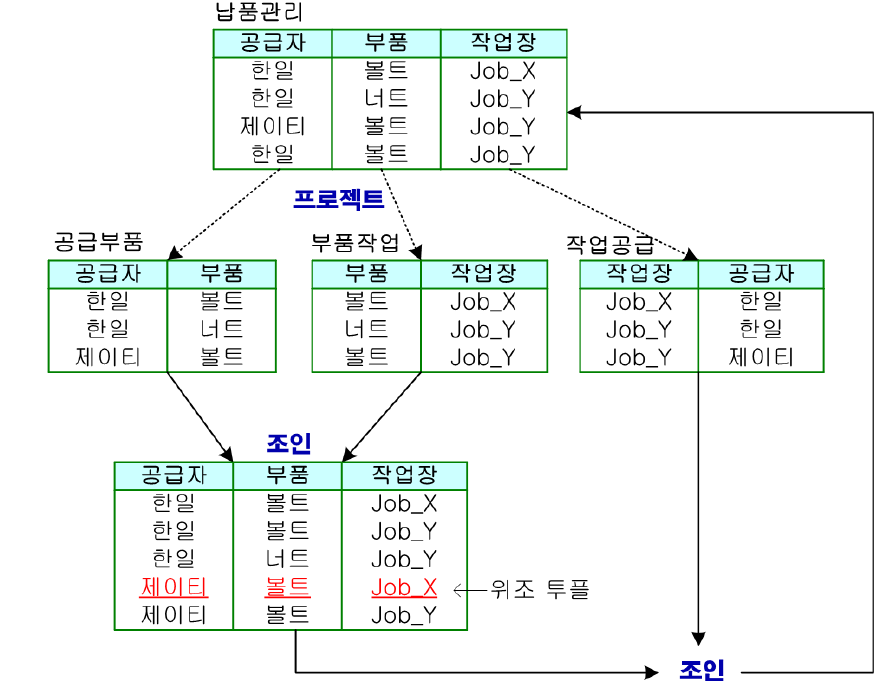
납품관리 릴레이션을 3개로 나눈 공급부품, 부품작업, 작업공급 릴레이션이 있는데 이 3개의 릴레이션을 모두 조인하면 결국 원래의 납품관리 릴레이션이 나온다. 이러한 관계를 조인 종속 이라고 한다.
어떤 릴레이션 R에 대해 프로젝트한 n개의 부분집합들을 모두 조인한 결과가 이 릴레이션 R과 똑같이 된다면 R은 조인 종속을 만족한다고 한다.
그러나 이런 식으로 계속해서 작게 분해하는 것에 대한 별다른 이점이 없어 현실적으로 잘 이용되지 않는다.
요약
- 비정규형 테이블의 모든 도메인이 원자값이 되게끔 수정 ->
1NF - 1NF의
부분 함수 종속을 제거 ->2NF - 2NF의
이행적 함수 종속을 제거 ->3NF - 3NF의 모든 결정자가 후보키가 되도록 분해 ->
BCNF - BCNF가 다치 종속을 갖지 않도록 분해 ->
4NF - 4NF를 조인 종속을 만족하는 n-분해 릴레이션으로 분해 ->
5NF