2023. 04. 14.
동적 계획법 Dynamic Programming 📌
동적계획법은 복잡한 문제를 여러 개의 간단한 문제로 분리하여 부분의 문제들을 해결함으로써 최종적으로 복잡한 문제의 답을 구하는 방법이다.
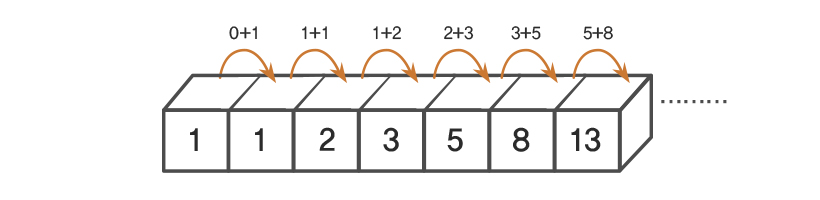
피보나치 수열
# 피보나치 함수를 재귀 함수로 구현
def fibo(x):
if x == 1 or x == 2:
return 1
return fibo(x-1) + fibo(x-2)위 코드와 같이 피보나치 수열의 소스코드를 작성하면 n이 커지면 커질수록 수행 시간이 기하급수적으로 늘어나게 된다. 이처럼 피보나치 수열을 재귀 함수를 사용해 만들 수 있지만, 단순히 매번 계산하도록 하면 문제를 효율적으로 해결할 수 없다. 이러한 경우 다이나믹 프로그래밍을 사용하면 효율적으로 해결할 수 있다.
동적 계획법의 핵심 이론
📢 동적 계획법의 원리
- 큰 문제를 작은 문제로 나눌 수 있어야 한다.
- 작은 문제들이 반복돼 나타나고 사용되며 이 작은 문제들의 결과값은 항상 같아야 한다.
- 모든 작은 문제들은 한 번만 계산해 DP 테이블에 저장하며 추후 재사용할 때는 DP 테이블을 이용한다. 이를 메모이제이션 기법이라고 한다.
- 동적 계획법은 탑-다운 방식과 바텀-업 방식으로 구현할 수 있다.
📢 동적 계획법의 접근 방법 - 피보나치 수열
1. 동적 계획법으로 풀 수 있는 지 확인하기
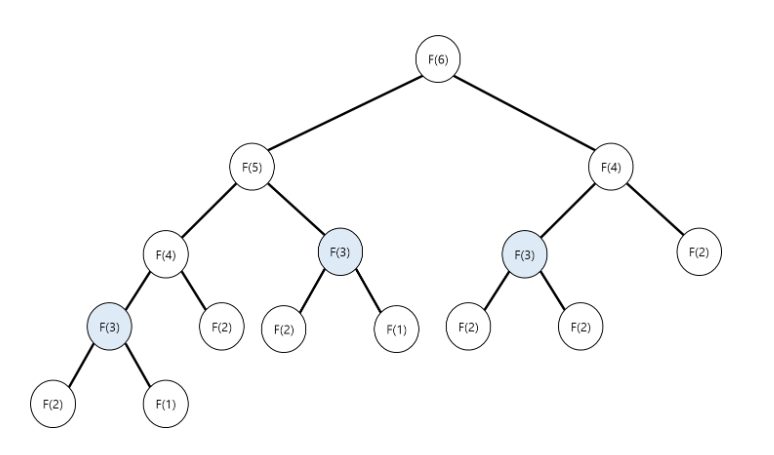
- 6번 째 피보나치 수열은 5번째 피보나치 수열과 4번째 피보나치 수열을 구하는 작은 문제로 나눌 수 있고, 수열의 값은 항상 같기 때문에 동적 계획법으로 풀 수 있다.
2. 점화식 세우기
- 점화식을 세울 때는 논리적으로 전체 문제를 나누고, 전체 문제와 부분 문제 간의 인과 관계를 파악해야 한다.
3. 메모이제이션 원리 이해하기
- 메모이제이션은 부분 문제를 풀었을 때 이 문제를 DP 테이블에 저장해 놓고 다음에 같은 문제가 나왔을 때 다시 계산하지 않고 DP 테이블의 값을 이용하는 것을 말한다. 이러한 방식을 사용하면 불필요한 연산과 탐색이 줄어들어 시간 복잡도 측면에서 많은 이점을 가질 수 있다.
4. 톱-다운 / 바텀-업 방식으로 구현
- 톱-다운 방식
-
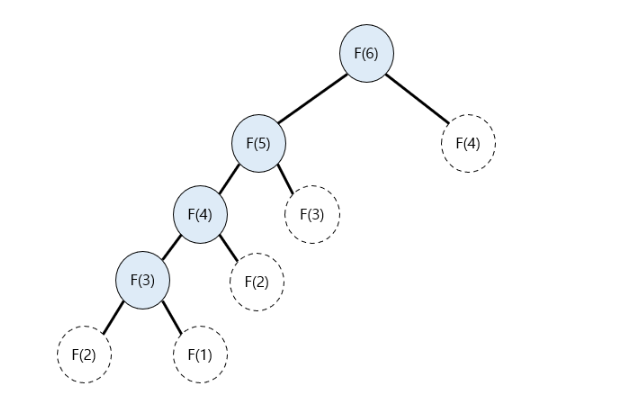
톱-다운 방식은 말 그대로 위에서부터 문제를 파악해 내려오는 방식으로, 주로 재귀 함수 형태로 코드를 구현한다. 코드의 가독성이 좋고 이해하기 쉽지만 재귀함수의 형태로 구현돼있기 때문에 재귀의 깊이가 매우 깊어질 경우 런타임 에러가 발생할 수 있다.
-
F(1)을 구한 다음 F(2)를 푸는 데 사용되고, F(2)의 값이 F(3)를 푸는 데 사용되는 방식으로 이어진다.
n = int(input())
# DP 테이블 초기화
D = [-1] * (n+1)
D[0] = 0
D[1] = 1
def fibo(n):
if D[n] != -1: # 기존에 계산한 적이 있는 부분의 문제는 다시 계산하지 않고 리턴
return D[n]
# 메모이제이션: 구한 값을 바로 리턴하지 않고 DP 테이블에 저장한 후 리턴
D[n] = fibo(n-2) + fibo(n-1)
return D[n]
fibo(n)
print(D[n])- 바텀-업 방식
- 바텀-업 방식은 톱-다운 방식과 반대로 가장 작은 부분 문제로부터 문제를 해결하면서 점점 큰 문제로 확장해 나가는 방식으로 주로 반복문의 형태로 구현한다.
n = int(input())
# DP 테이블 초기화
D = [-1] * (n+1)
D[0] = 0
D[1] = 1
for i in range(2, n+1):
D[i] = D[i-2] + D[i-1]
print(D[n])2023. 04. 14. 오늘의 문제풀이 ✍
BOJ 14501 - 퇴사
n = int(input())
t = []
p = []
dp = [0] * (n+1)
max_value = 0
for i in range(n):
a,b = map(int,input().split())
t.append(a)
p.append(b)
for i in range(n-1,-1,-1):
time = t[i] + i
if time <= n:
dp[i] = max(p[i] + dp[time], max_value)
max_value = dp[i]
else:
dp[i] = max_value
print(max_value)BOJ 2193 - 이친수
import sys
input = sys.stdin.readline
n = int(input())
D = [[0] * 2 for i in range(n+1)]
result = 0
# D[i][0] = i길이에서 끝이 0으로 끝나는 이친수의 개수
# D[i][1] = i길이에서 끝이 1로 끝나는 이친수의 개수
D[1][1] = 1 # 1자리 이친수는 1가지만 있음
D[1][0] = 0 # 0으로 끝나는 1자리 이친수는 없음
# 2자리에서 n자리까지
for i in range(2, n+1):
D[i][0] = D[i-1][1] + D[i-1][0] # 0으로 끝나는 이친수는 앞이 1과 0 둘다 됨
D[i][1] = D[i-1][0] # 1로 끝나는 이친수는 앞이 0일 경우만 됨
result = D[n][0] + D[n][1]
print(result)BOJ 13398 - 연속합2
import sys
input = sys.stdin.readline
n = int(input())
datas = list(map(int,input().split()))
# 오른쪽에서 index를 포함한 최대 연속 합 구하기
L = [0] * n
L[0] = datas[0]
result = L[0]
for i in range(1, n):
L[i] = max(datas[i], L[i-1] + datas[i])
result = max(result, L[i])
# 왼쪽으로 index를 포함한 최대 연속 합 구하기
R = [0] * n
R[-1] = datas[-1]
for j in range(n-2, -1, -1):
R[j] = max(datas[j], R[j+1] + datas[j])
# L[i-1] + R[i+1] 2개의 구간 합 리스트를 더하면 i번째 값을 제거한 효과
for k in range(1, n-1):
tmp = L[k-1] + R[k+1]
result = max(result, tmp)
print(result)BOJ 9252 - LCS2
출처