😁 그래프 최단 경로 알고리즘 - 다익스트라, 벨만포드, 플로이드워셜
거리가 짧다는 것의 기준
가중 그래프가 아닌 경우에는 경로 상에 있는 간선의 수가 적을수록 거리가 짧은 것이고
가중 그래프인 경우에는 경로 상에 있는 간선의 가중치 합이 작을 수록 거리가 짧은 것이다.
만약 음수 사이클이 존재한다면?
만약 가중치가 음수이고 사이클이 존재하면 사이클을 돌 때마다 음수가중치가 더해지기 때문에 사이클을 거칠수록 경로의 거리가 계속 줄어들게 된다.
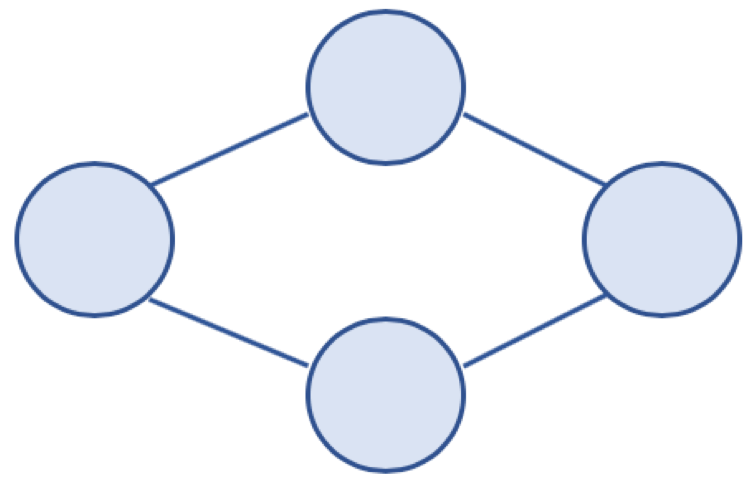
여기서 사이클은 위 사진과 같이 계속 한바퀴두바퀴 시작점으로 다시 돌아올 수 있는 걸 의미하고, 음수 사이클은 사이클 내에 있는 간선의 가중치 합이 음수인 사이클을 의미한다. 만약 음수 사이클이 아니라 양수 사이클이면 갈수록 최단 경로와 반대로 가중치가 늘어나므로 양수 사이클일 경우에는 생각하지 않아도 된다. 음수 사이클일 때는 경로를 지날 때마다 값이 작아지므로 최단 경로가 계속 업데이트 된다.
상황별 적용해야 될 최단 경로 알고리즘
2-1) 다익스트라 알고리즘
한 노드에서 다른 모든 노드까지의 최단 경로를 구하는 알고리즘이다.
- 사용할 수 있는 상황:
- 음수 간선이 존재하지 않을 때
다익스트라 알고리즘의 핵심은 가장 짧은 거리의 경로부터 탐색한다는 것이다.
가장 짧은 거리의 경로 순대로 탐색하려면 탐색 하려는 경로의 후보 중에서 거리가 가장 짧은 경로를 뽑아야 한다.
방법1) PriorityQueue 사용
from queue import PriorityQueue
INF = int(1e9)
N = 5
graph = [[] for _ in range(N)]
distance = [INF] * N
graph[0].append([1,5]); graph[0].append([3,1])
graph[1].append([2,2])
graph[2].append([4,2])
graph[3].append([1,2]); graph[3].append([4,7])
pq = PriorityQueue()
# [거리, 도착노드] 0에서 0까지 거리는 0
pq.put([0,0])
distance[0] = 0
while pq.queue:
cur_dist, cur_node = pq.get()
for node, dist in graph[cur_node]:
temp_dist = cur_dist + dist
if distance[node] > temp_dist:
pq.put([temp_dist, node])
distance[node] = temp_dist
print(distance)방법2) Heapq 사용
import heapq
INF = int(1e9)
N = 5
graph = [[] for _ in range(N)]
distance = [INF] * N
graph[0].append([1,5]); graph[0].append([3,1])
graph[1].append([2,2])
graph[2].append([4,2])
graph[3].append([1,2]); graph[3].append([4,7])
def dijkstra(start):
queue = []
distance[start] = 0
heapq.heappush(queue, [0,0])
while queue:
cur_dist, cur_node = heapq.heappop(queue)
for next_node, next_dist in graph[cur_node]:
temp_dist = cur_dist + next_dist
if temp_dist < distance[next_node]:
heapq.heappush(queue, [temp_dist, next_node])
distance[next_node] = temp_dist
return distance
print(dijkstra(0))다익스르타 알고리즘은 최대 간선의 개수만큼 pq에 경로의 후보가 들어간다. 그리고 가장 작은 원소를 뽑을 때는 logM만큼 든다. 근데 결국 간선의 개수는 N^2보다 작으므로 O(MlogM)이 아닌 O(MlogN)라고 할 수 있다.
다익스트라 알고리즘은 경로의 후보를 heap 에 저장해야 하므로 시간 복잡도는 O(MlogN)이다. (노드의 개수 N, 간선의 개수 M)
Priority Queue와 Heapq의 차이점
Priority Queue는 Thread-Safe하고 Heapq는 Non-Safe하다. Thread Safe 하다는 것은 반드시 확인 절차를 거쳐야 하기 때문에 확인하는 작업 때문에 더 느리다.
그렇기 때문에 Thread-Safe를 요구하는 상황에서는 Priority Queue를 사용하고 아니라면 heapq를 사용하는 것이 시간 효율적이다.
😀 다익스트라 알고리즘에서 음수 간선이 존재하면 안되는 이유
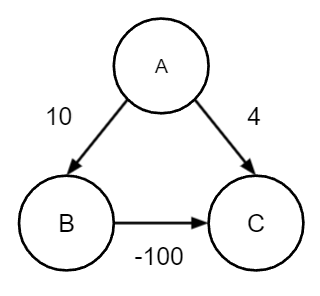
(사진 출처: kangworld.tistory.com)
위 사진에서 A에서 시작해 다익스트라 알고리즘을 수행한다고 생각해보자. 그러면 A와 인접한 B와 C는 10과 4로 최단거리가 업데이트가 되고, 그 다음으로 C를 방문해 C와 인접한 노드들과의 거리를 비교하며 거리를 업데이트 한다. 그 다음 B를 방문해 수행하면 B에서 C로는 거리 업데이트를 하지 않는다. 왜냐면 이미 전에 C를 방문했기 때문에 visited가 True이기 때문이다. 그렇기 때문에 음수 간선이 하나라도 존재한다면 다익스트라 알고리즘을 사용할 수 없다!
2-2) 벨만-포드 알고리즘 O(NM)
한 노드에서 다른 모든 노드까지의 최단 경로를 구하는 알고리즘이다.
- 사용할 수 있는 상황:
- 음수 사이클이 존재하지 않을 때
2-3) 플로이드-워셜 알고리즘 O(N^3)
모든 노드에서 다른 모든 노드까지의 최단 경로를 구하는 알고리즘이다.
- 사용할 수 있는 상황:
- 음수 사이클이 존재하지 않을 때
다익스트라 알고리즘은 음수 간선이 존재할 경우엔 사용하지 못하지만, 벨만-포드와 플로이드-워셜 알고리즘은 음수 간선이 존재해도는 되지만 음수 사이클(사이클에 존재하는 간선의 총합이 음수일 때)이 존재할 경우에는 사용하지 못한다.
🐥 최단 경로 알고리즘을 사용해야 하는 상황
Case1) 한 노드에서 다른 (모든) 노드까지의 최단 경로/거리 (음수 간선 존재 X)
음수 간선이 존재하지 않으면 다익스트라, 벨만포드를 사용할 수 있다. 하지만 시간 복잡도상 더 효율적인 다익스트라 알고리즘을 사용하면 된다.
Case2) 한 노드에서 다른 (모든) 노드까지의 최단 경로/거리 (음수 간선 존재 O)
한 노드에서 다른 모든 노드까지의 최단 경로를 구할 때는 다익스트라와 벨만포드를 사용할 수 있는데, 음수 간선이 존재한다면 벨만-포드 알고리즘을 사용해야 한다.
Case3) 모든 노드에서 모든 노드까지의 최단 경로/거리
모든 노드에서 모든 노드까지의 거리는 당연히 플로이드-워셜 알고리즘을 사용하면 된다.
😐 여기서 벨만-포드를 사용하면 안되냐?라고 생각하면 일반적으로 간선의 개수는 노드의 개수보다 많다. 그렇기 때문에 벨만 포드를 사용하면 O(N^2*M)이 되므로 플로이드-워셜 알고리즘보다 비효율적이다. 그러면 다익스트라 알고리즘을 사용하면 더 효율적일까?? 더 효율적인 상황이 있겠지만 N번 더 반복을 해야하므로 웬만하면 플로이드-워셜 알고리즘을 사용하는 게 효율적이다. 결론은 그냥 플로이드-워셜 알고리즘을 사용하자.
🍗 문제 풀이
문제 1) BOJ 13549
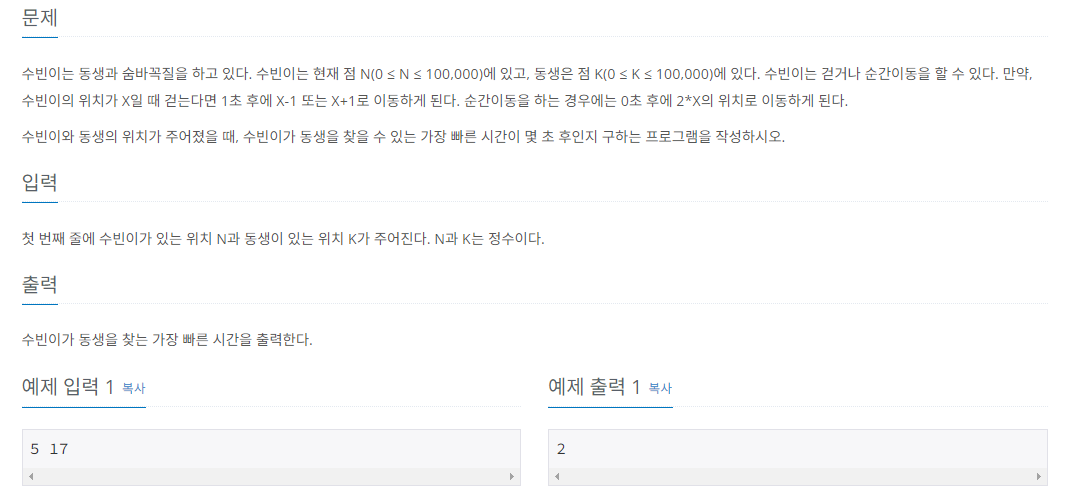
위 문제를 풀기 전 문제가 그래프 문제임을 알아차리는 것이 중요하다. 이 문제에선 각 노드가 0에서 10만까지 있는데 여기서 한 노드에서 한 노드까지의 최단 시간 = 최단 거리를 구하는 문제로 변환할 수 있다. 그러면, BFS로도 풀 수 있겠지만 이 문제에선 가중치가 존재한다. 걸을 땐 +1 -1, 순간이동 시에는 2를 곱하고 각각 가중치가 다르기 때문에 BFS로는 풀지 못한다.
BOJ1697
수빈이는 동생과 숨바꼭질을 하고 있다. 수빈이는 현재 점 N(0 ≤ N ≤ 100,000)에 있고, 동생은 점 K(0 ≤ K ≤ 100,000)에 있다. 수빈이는 걷거나 순간이동을 할 수 있다. 만약, 수빈이의 위치가 X일 때 걷는다면 1초 후에 X-1 또는 X+1로 이동하게 된다. 순간이동을 하는 경우에는 1초 후에 2*X의 위치로 이동하게 된다.
수빈이와 동생의 위치가 주어졌을 때, 수빈이가 동생을 찾을 수 있는 가장 빠른 시간이 몇 초 후인지 구하는 프로그램을 작성하시오.
여기 문제에선 다른 노드로 움직일 때의 가중치가 +1로 다 같은 걸 알 수 있다. 여기선 그럼 BFS로 문제를 해결할 수 있는 것이다.
다시 이 문제로 돌아오면 노드는 10만개, 그럼 간선의 개수는 각 노드마다 3가지 종류가 있는 것이다. +1, -1, 2 이런 3가지 갈래로 나뉘는데 그럼 대충 간선의 개수는 3 * 10만 = 30만으로 다익스트라 알고리즘을 사용해도 충분히 시간 내에 문제를 풀 수 있음을 알 수 있다.
import sys
import heapq
input = sys.stdin.readline
N,K = map(int,input().split())
INF = 1e9
MAX = 100000
time = [INF] * (MAX + 1)
queue = []
time[N] = 0
heapq.heappush(queue, [0, N])
while queue:
cur_time, cur_node = heapq.heappop(queue)
nexts = [
(cur_time, 2 * cur_node),
(cur_time + 1, cur_node + 1),
(cur_time + 1, cur_node - 1)
]
for next_time, next_node in nexts:
if 0 <= next_node <= MAX and next_time < time[next_node]:
time[next_node] = next_time
heapq.heappush(queue, [next_time, next_node])
print(time[K])다음 노드로 이동할 때마다 가중치가 각각 다르므로 nexts라는 것에 다음 상태 => (시간, 노드)를 미리 정의해 만약 시간이 더 작으면 갱신하는 형태로 다익스트라 알고리즘 형태로 코드를 구현하면 된다. 추가로 다음 노드가 유효한 노드인지 확인하는 작업을 빼먹지 않도록 주의하자.
참고
세계 대회 진출자가 알려주는 코딩테스트 A to Z (with Python)
