💡 Info
- 난이도: Lv2
프로그래머스 링크: https://school.programmers.co.kr/learn/courses/30/lessons/389480
풀이 링크(GitHub): hayannn/CodingTest_Java/프로그래머스/2/완전범죄
입출력 조건
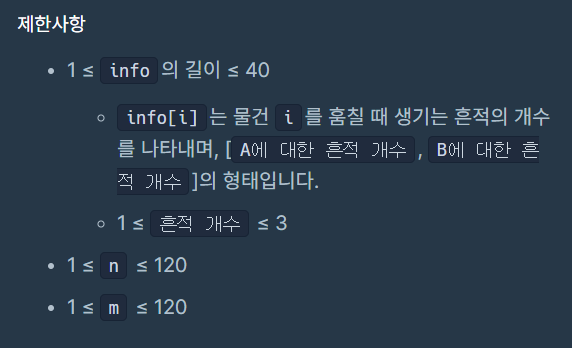
입출력 예시



문제 이해
- DP를 이용하여 두 도둑 모두 경찰에 붙잡히지 않도록 모든 물건을 훔쳤을 때, A도둑이 남긴 흔적 누적 개수 최솟값 구하기
알고리즘
풀이 시간 : 23분
dp[i][j] = i번째 물건까지 처리 -> B의 흔적 총합이 j인 상황에서 A 흔적 총합의 최솟값 구하기- A가 훔치는 경우와 B가 훔치는 경우로 나눠 처리
- A :
dp[i][j] = Math.min(dp[i][j], dp[i-1][j] + a) - B :
dp[i][j + b] = Math.min(dp[i][j + b], dp[i-1][j])
- A :
- 모든 물건 처리 후 ->
dp[size][j]의 최솟값을 찾아서 n 이상이면 -1 반환, 그렇지 않으면 최솟값 자체를 반환
import java.util.*;
class Solution {
static final int INF = 100000;
public int solution(int[][] info, int n, int m) {
int size = info.length;
int[][] dp = new int[size + 1][m];
for (int i = 0; i <= size; i++) {
Arrays.fill(dp[i], INF);
}
dp[0][0] = 0;
for (int i = 1; i <= size; i++) {
int a = info[i-1][0]; // A 흔적
int b = info[i-1][1]; // B 흔적
for (int j = 0; j < m; j++) {
// A가 선택
dp[i][j] = Math.min(dp[i][j], dp[i-1][j] + a);
// B가 선택
if (j + b < m) {
dp[i][j + b] = Math.min(dp[i][j + b], dp[i-1][j]);
}
}
}
int min = INF;
for (int j = 0; j < m; j++) {
min = Math.min(dp[size][j], min);
}
return min >= n ? -1 : min;
}
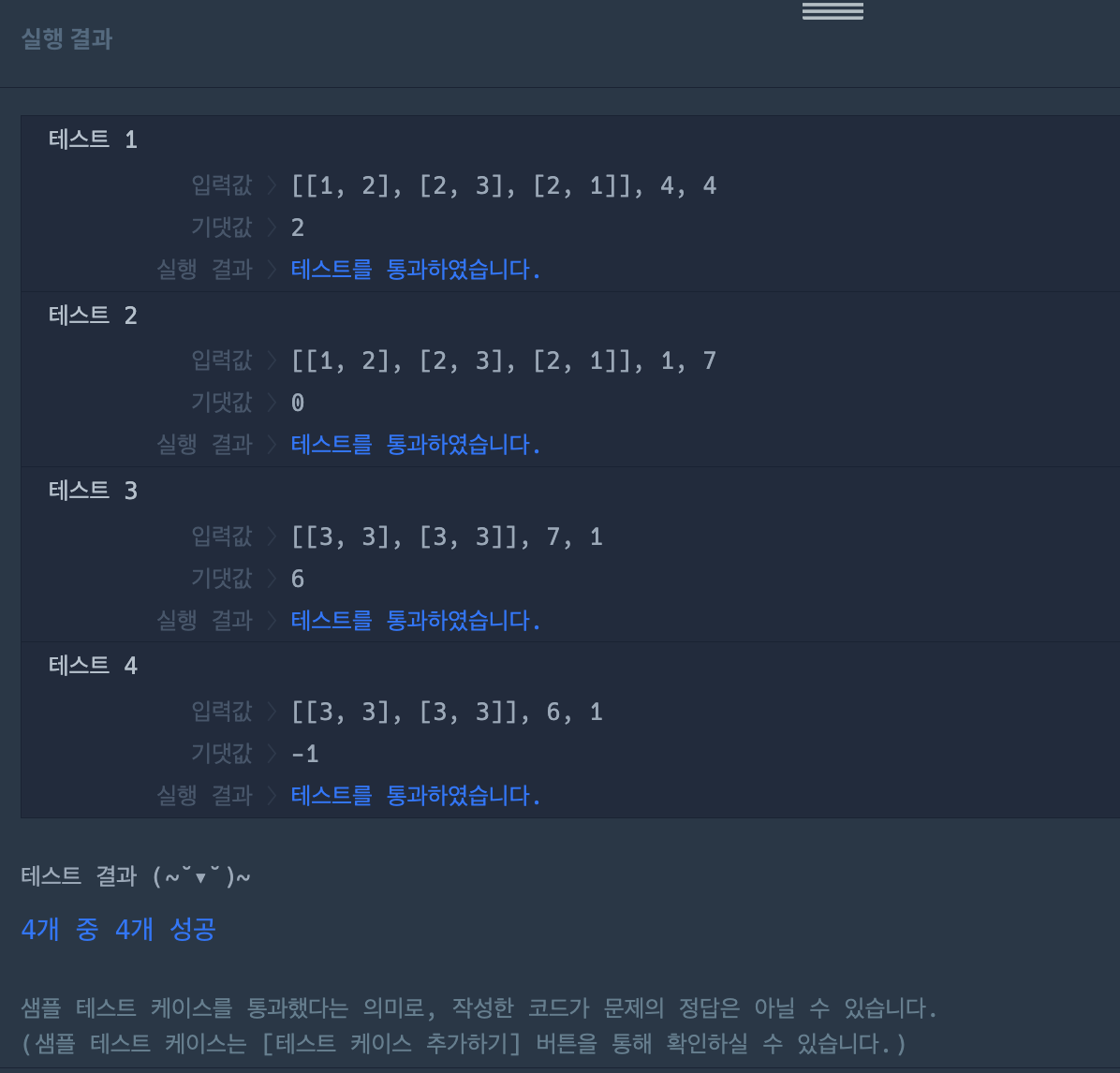
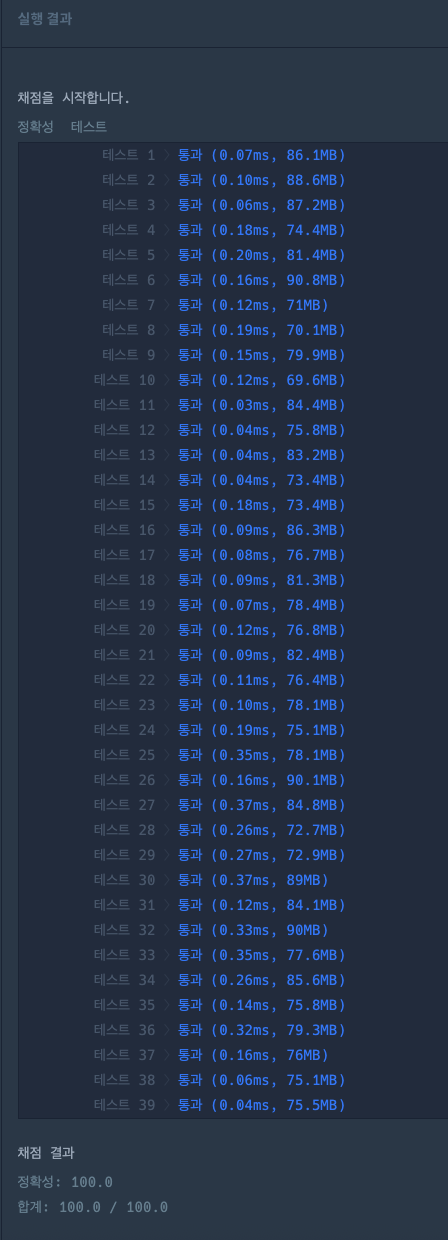
}결과
✍️ 다른 풀이 - 최적화
- B 흔적 제한 내에서 A가 절약할 수 있는 최대 흔적 개수를 구해 -> 전체 A 흔적에서 빼는 방식이기 때문에 더 효율적!
import java.util.*;
class Solution {
public int solution(int[][] info, int n, int m) {
int thingCount = info.length;
int[] dp = new int[m];
// 모든 물건을 A가 훔쳤을 때 총 흔적 개수
int maxATrace = 0;
for (int i = 0; i < thingCount; i++) {
maxATrace += info[i][0];
}
// 배낭 DP: B의 가중치로 접근하면서 A의 절약값 최대치 구하기
for (int i = 0; i < thingCount; i++) {
int aTrace = info[i][0];
int bTrace = info[i][1];
for (int j = m - 1; j >= bTrace; j--) {
dp[j] = Math.max(dp[j], dp[j - bTrace] + aTrace);
}
}
int answer = maxATrace - dp[m - 1];
return answer >= n ? -1 : answer;
}
}