🏆 [Baekjoon / Java] 1799. 비숍

문제 설명

💡 Info

• 난이도 : 플래티넘 V
• 시간 제한 : 10초
• 메모리 제한 : 128MB
• 백준 링크: https://www.acmicpc.net/problem/1799
  풀이 링크(GitHub): hayannn/CodingTest_Java/백준/Platinum/1799. 비숍

내용

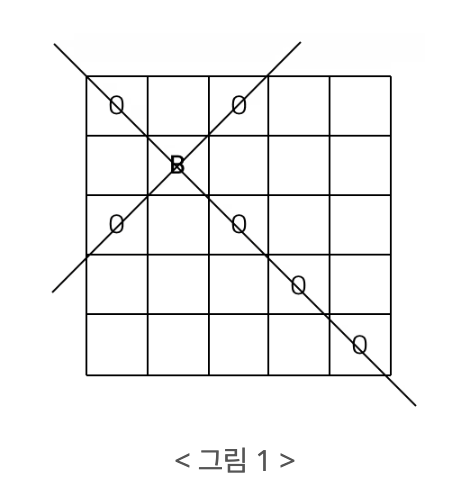
서양 장기인 체스에는 대각선 방향으로 움직일 수 있는 비숍(bishop)이 있다. < 그림 1 >과 같은 정사각형 체스판 위에 B라고 표시된 곳에 비숍이 있을 때 비숍은 대각선 방향으로 움직여 O로 표시된 칸에 있는 다른 말을 잡을 수 있다.

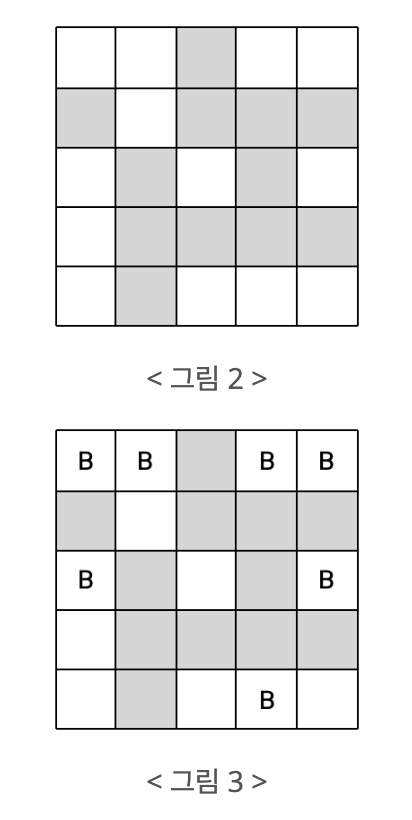
그런데 체스판 위에는 비숍이 놓일 수 없는 곳이 있다. < 그림 2 >에서 체스판에 색칠된 부분은 비숍이 놓일 수 없다고 하자. 이와 같은 체스판에 서로가 서로를 잡을 수 없도록 하면서 비숍을 놓는다면 < 그림 3 >과 같이 최대 7개의 비숍을 놓을 수 있다. 색칠된 부분에는 비숍이 놓일 수 없지만 지나갈 수는 있다.

정사각형 체스판의 한 변에 놓인 칸의 개수를 체스판의 크기라고 한다. 체스판의 크기와 체스판 각 칸에 비숍을 놓을 수 있는지 없는지에 대한 정보가 주어질 때, 서로가 서로를 잡을 수 없는 위치에 놓을 수 있는 비숍의 최대 개수를 구하는 프로그램을 작성하시오.

📥입력 조건

• 첫째 줄에 체스판의 크기가 주어진다. 체스판의 크기는 10이하의 자연수이다.
• 둘째 줄부터 아래의 예와 같이 체스판의 각 칸에 비숍을 놓을 수 있는지 없는지에 대한 정보가 체스판 한 줄 단위로 한 줄씩 주어진다.
• 비숍을 놓을 수 있는 곳에는 1, 비숍을 놓을 수 없는 곳에는 0이 빈칸을 사이에 두고 주어진다.

5
1 1 0 1 1
0 1 0 0 0
1 0 1 0 1
1 0 0 0 0
1 0 1 1 1

📤출력 조건

• 첫째 줄에 주어진 체스판 위에 놓을 수 있는 비숍의 최대 개수를 출력한다.

7

문제 이해

• 비숍이 가능한 최대의 수를 찾는 문제

알고리즘 및 최종 풀이

실제 풀이 시간 : 1시간 2분(첫 풀이 시간 포함)

• 입력

  • N, 비숍 가능 여부 입력

• 계산

  • initializeColorPattern()
    • 칸 색상 결정
  • 검정, 흰색에 따라서 backtrack()로 가능한 최대 비숍 개수 구하기
    • 비숍을 놓아도 되는지 확인 -> 된다면 놓고 난 후 재귀 돌리기
    • 색상별 최대 비숍 개수 저장(maxBlackBishops, maxWhiteBishops)

• 출력

  • 검정과 흰색에 놓을 수 있는 최대 비숍의 개수를 합해서 출력

import java.io.*;
import java.util.*;

public class Main {
    static int N;
    static int maxBishops;
    static int maxBlackBishops;
    static int maxWhiteBishops;

    static int[][] board;
    static int[][] colorPattern;
    static boolean[][] occupied;
    static int[][] directions = {{-1,-1},{-1,1},{1,-1},{1,1}};

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());
        board = new int[N][N];
        occupied = new boolean[N][N];
        
        for (int i = 0; i < N; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            for (int j = 0; j < N; j++) {
                board[i][j] = Integer.parseInt(st.nextToken());
            }
        }
        
        colorPattern = new int[N][N];
        initializeColorPattern();

        backtrack(0, 0, 0, 0);
        backtrack(0, 1, 1, 0);

        maxBishops = maxBlackBishops + maxWhiteBishops;
        System.out.println(maxBishops);
    }

    static void initializeColorPattern() {
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                colorPattern[i][j] = (i + j) % 2;
            }
        }
    }

    static void backtrack(int y, int x, int color, int count) {
        if (y >= N) {
            if (color == 0) {
                maxBlackBishops = Math.max(maxBlackBishops, count);
            } else {
                maxWhiteBishops = Math.max(maxWhiteBishops, count);
            }
            return;
        }

        int nextX = x + 2;
        int nextY = y;

        if (nextX >= N) {
            nextY++;
            if (nextY < N) {
                nextX = colorPattern[nextY][0] == color ? 0 : 1;
            }
        }

        if (board[y][x] == 0) {
            backtrack(nextY, nextX, color, count);
            return;
        }

        if (isValidPosition(y, x)) {
            occupied[y][x] = true;
            backtrack(nextY, nextX, color, count + 1);
            occupied[y][x] = false;
        }

        backtrack(nextY, nextX, color, count);
    }

    static boolean isValidPosition(int x, int y) {
        int directionCount = 0;
        for (int dir = 0; dir < 4; dir++) {
            if (canMove(x, y, dir)) directionCount++;
        }
        return directionCount == 4;
    }

    static boolean canMove(int x, int y, int dir) {
        int nx = x;
        int ny = y;
        while (true) {
            nx += directions[dir][0];
            ny += directions[dir][1];
            if (nx < 0 || nx >= N || ny < 0 || ny >= N) break;
            if (occupied[nx][ny]) return false;
        }
        return true;
    }
}