이진 분류에 따른 회귀인 로지스틱 회귀
예를 들어 합격/불합격 결과의 값을 내는 함수라면 로지스틱 회귀를 사용
import numpy as np
import matplotlib.pyplot as pltdef sigmoid(x):
return 1/(1+np.exp(-x))
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y, 'g')
plt.plot([0,0],[1.0,0.0], ':') # 가운데 점선 추가
plt.title('Sigmoid Function')
plt.show()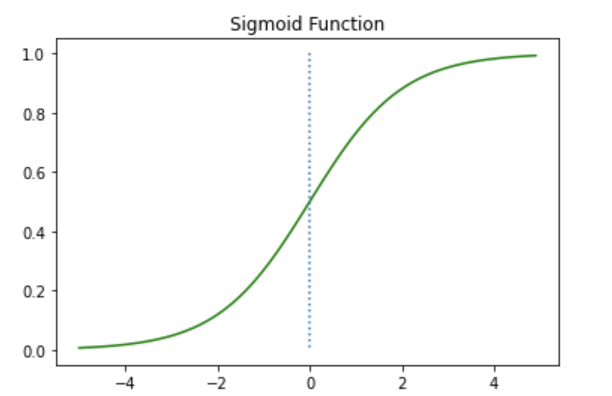
가중치에 따른 변화
def sigmoid(x):
return 1/(1+np.exp(-x))
x = np.arange(-5.0, 5.0, 0.1)
y1 = sigmoid(0.5*x)
y2 = sigmoid(x)
y3 = sigmoid(2*x)
plt.plot(x, y1, 'r', linestyle='--') # w의 값이 0.5일때
plt.plot(x, y2, 'g') # w의 값이 1일때
plt.plot(x, y3, 'b', linestyle='--') # w의 값이 2일때
plt.plot([0,0],[1.0,0.0], ':') # 가운데 점선 추가
plt.title('Sigmoid Function')
plt.show()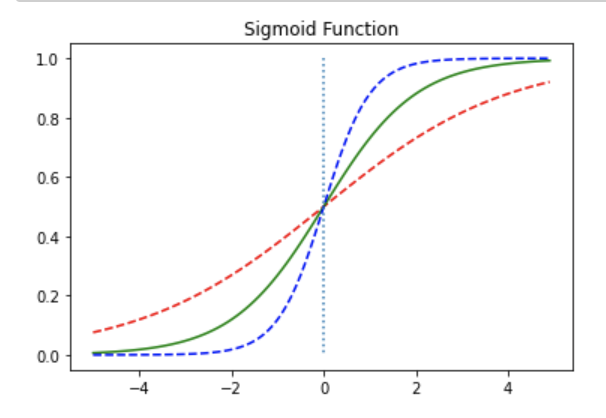
가 0.5일 때 빨간색, 1일 때 초록, 2일 때 파란색
--> 값에 따라 경사도가 달라진다.
에 따른 변화
def sigmoid(x):
return 1/(1+np.exp(-x))
x = np.arange(-5.0, 5.0, 0.1)
y1 = sigmoid(x+0.5)
y2 = sigmoid(x+1)
y3 = sigmoid(x+1.5)
plt.plot(x, y1, 'r', linestyle='--') # x + 0.5
plt.plot(x, y2, 'g') # x + 1
plt.plot(x, y3, 'b', linestyle='--') # x + 1.5
plt.plot([0,0],[1.0,0.0], ':') # 가운데 점선 추가
plt.title('Sigmoid Function')
plt.show()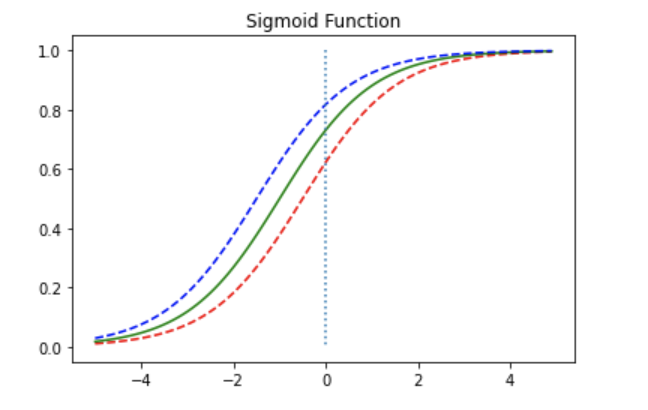
비용함수
로지스틱에서 MSE는 로컬 미니멈에 빠질 수 있기 때문에 다른 함수를 사용
시그모이드는 0과 1사이의 값을 반환하므로 실제값이 0일 때 y값이 1에 가까워지면 오차가 커진다.
케라스로 구현
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras import optimizers
x = np.array([-50, -40, -30, -20, -10, -5, 0, 5, 10, 20, 30, 40, 50])
y = np.array([0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1]) # 숫자 10부터 1
model = Sequential()
model.add(Dense(1, input_dim=1, activation='sigmoid'))
sgd = optimizers.SGD(lr=0.01)
model.compile(optimizer=sgd, loss='binary_crossentropy', metrics=['binary_accuracy'])
model.fit(x, y, epochs=200)plt.plot(x, model.predict(x), 'b', x,y, 'k.')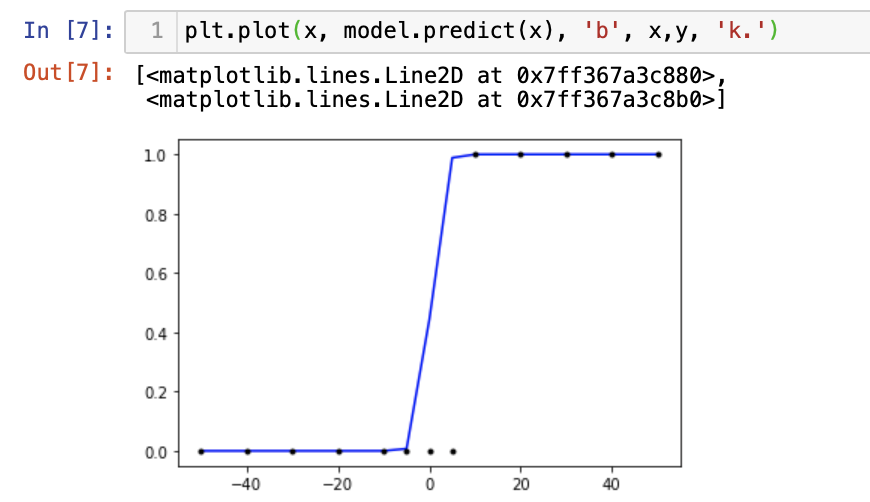
print(model.predict([1, 2, 3, 4, 4.5]))
print(model.predict([11, 21, 31, 41, 500]))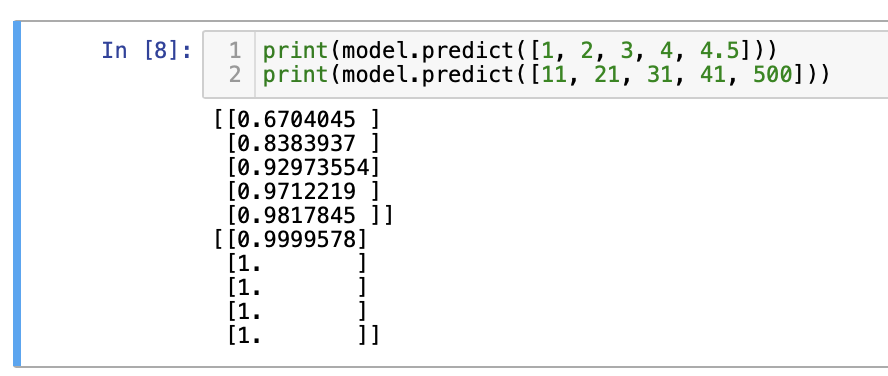
다중 입력
다중 선형 회귀
import numpy as np
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras import optimizers독립변수 3개인 선형회귀
세 시험에 대한 최종점수 계산
# 중간 고사, 기말 고사, 가산점 점수
X = np.array([[70,85,11], [71,89,18], [50,80,20], [99,20,10], [50,10,10]])
y = np.array([73, 82 ,72, 57, 34]) # 최종 성적
model = Sequential()
model.add(Dense(1, input_dim=3, activation='linear'))
sgd = optimizers.SGD(lr=0.0001)
model.compile(optimizer=sgd, loss='mse', metrics=['mse'])
model.fit(X, y, epochs=2000)X_test = np.array([[20,99,10], [40,50,20]])
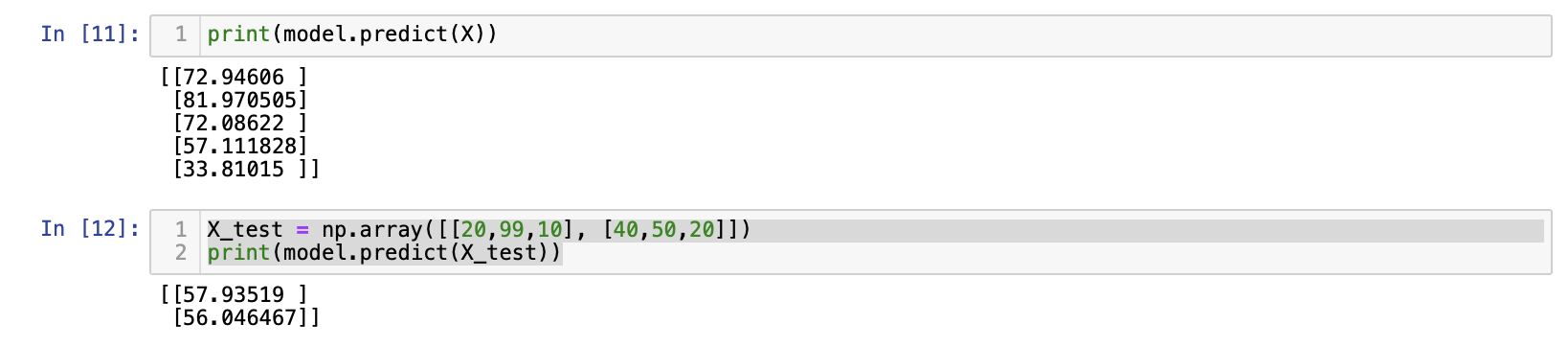
print(model.predict(X_test))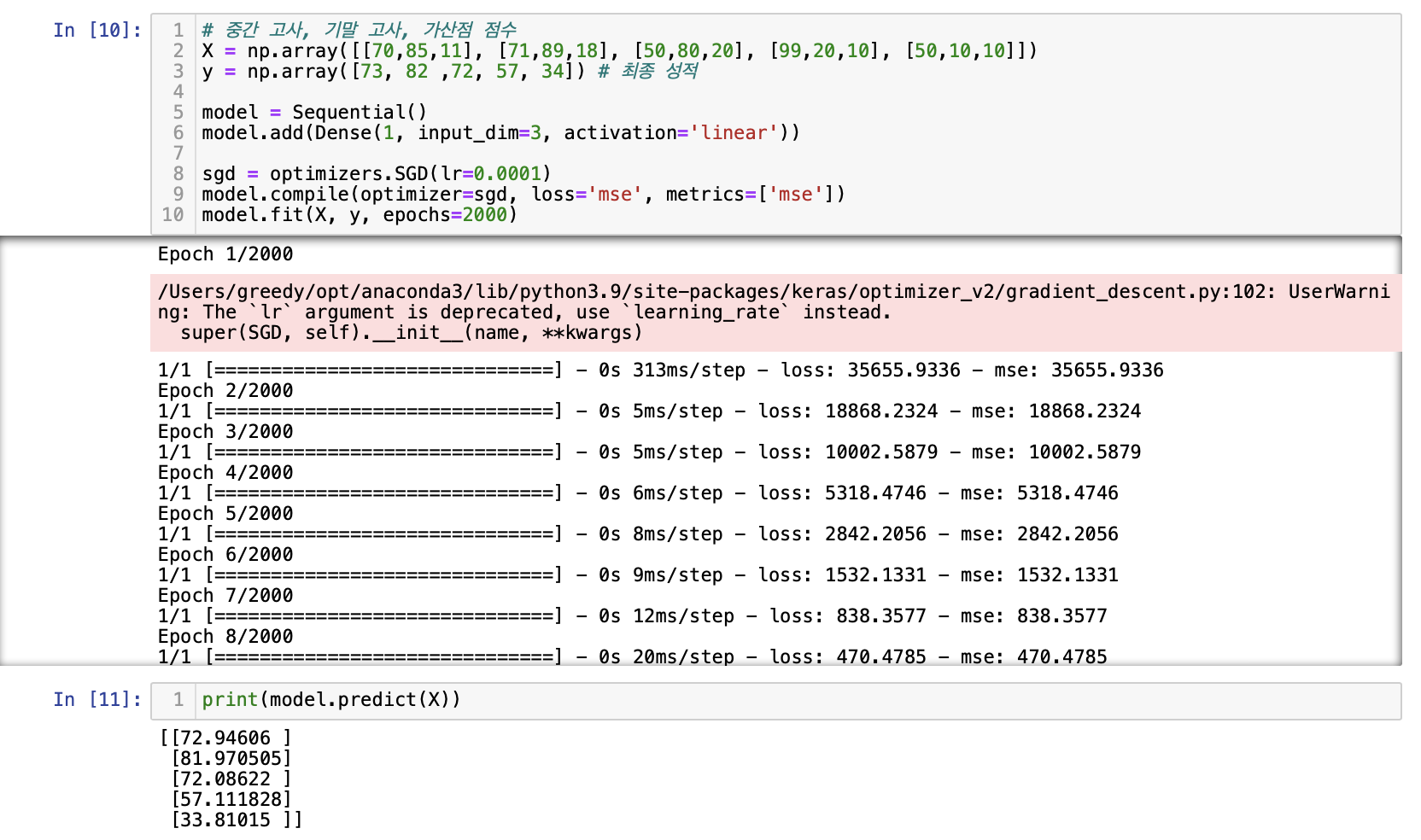
다중 로지스틱

독립 변수 2개(꽃받침 길이, 꽃잎 길이로 꽃의 종류를 파악)
두 입력의 합이 이상이면 1인 로직
X = np.array([[0, 0], [0, 1], [1, 0], [0, 2], [1, 1], [2, 0]])
y = np.array([0, 0, 0, 1, 1, 1])
model = Sequential()
model.add(Dense(1, input_dim=2, activation='sigmoid'))
model.compile(optimizer='sgd', loss='binary_crossentropy', metrics=['binary_accuracy'])
model.fit(X, y, epochs=2000)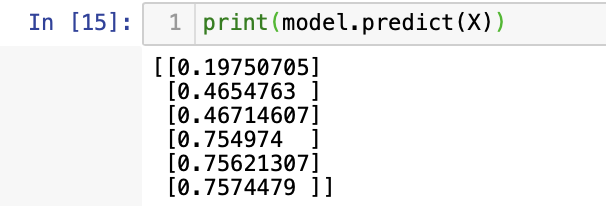
인공 신경망 다이어그램

벡터와 행렬 연산
벡터 : 크기와 방향을 가진 양
행렬 : 행과 열을 가진 2차원의 형상
3차원 이상의 배열을 이해하기 위해 텐서
import numpy as np
d = np.array(5)
print('텐서의 차원 :',d.ndim)
print('텐서의 크기(shape) :',d.shape)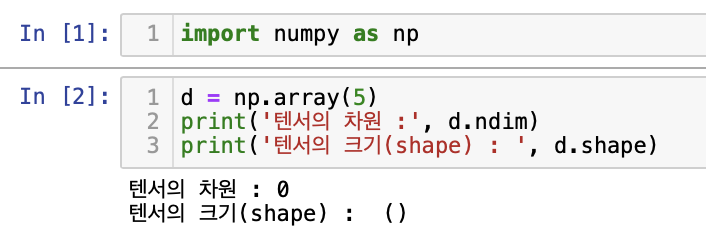
ndim에서의 숫자는 차원(axis의 갯수)

3차원 이상은 텐서로 보통 부른다.
연산
A = np.array([8, 4, 5])
B = np.array([1, 2, 3])
print('두 벡터의 합 :',A+B)
print('두 벡터의 차 :',A-B)두 행렬의 합 : [9 6 8]
두 행렬의 차 : [7 2 2]A = np.array([[10, 20, 30, 40], [50, 60, 70, 80]])
B = np.array([[5, 6, 7, 8],[1, 2, 3, 4]])
print('두 행렬의 합 :')
print(A + B)
print('두 행렬의 차 :')
print(A - B)두 행렬의 합 :
[[15 26 37 48]
[51 62 73 84]]
두 행렬의 차 :
[[ 5 14 23 32]
[49 58 67 76]]벡터의 내적은 dot으로 표현하며 두 벡터의 차원이 같아야 한다.
내적결과는 스칼라로 나타난다.
A = np.array([1, 2, 3])
B = np.array([4, 5, 6])
print('두 벡터의 내적 :',np.dot(A, B))두 벡터의 내적 : 32행렬의 곱셈은 왼쪽 행렬의 행벡터와 오른쪽 행렬의 열벡터의 내적이 결과 행렬의 원소로 나타남
A = np.array([[1, 3],[2, 4]])
B = np.array([[5, 7],[6, 8]])
print('두 행렬의 행렬곱 :')
print(np.matmul(A, B))두 행렬의 행렬곱 :
[[23 31]
[34 46]]다중선형회귀의 모습을 행렬의 곱으로 나타낼 수 있다.
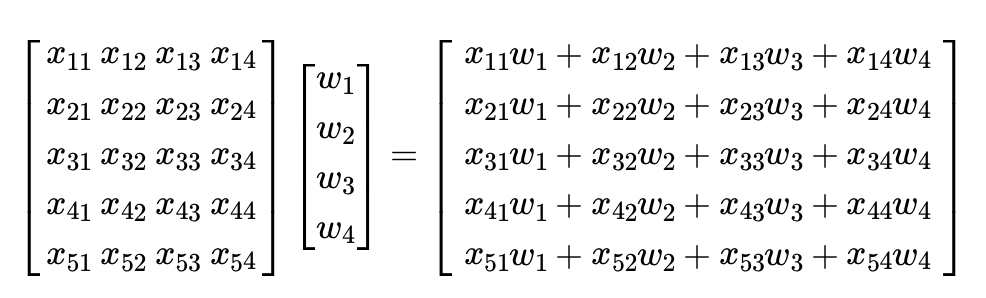
입력 행렬 와 가중치 벡터 의 곱
위 식에 편향 벡터 를 더하면
소프트맥스 회귀
로지스틱이 이진분류라면 3개 이상의 선택지 중 1개를 고르는 다중 클래스 분류 문제는 소프트맥스
소프트맥스 함수
- K개의 선택지일 때 입력치의 차원은 K
- 여러 데이터를 K개로 축소하기 위해 가중치 곱
- 실제값은 원-핫 벡터로 표현한다
- 예측값과 실제값과의 차이는 오차이며, 이로부터 가중치를 업데이트한다.
- 비용함수로는 크로스 엔트로피 함수를 사용한다.
크로스 엔트로피 함수
제대로 예측하면 이 되고 예측치와 실제값이 같다는 의미이다.
실습
데이터 https://www.kaggle.com/saurabh00007/iriscsv
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import urllib.request
from sklearn.model_selection import train_test_split
from tensorflow.keras.utils import to_categoricalurllib.request.urlretrieve("https://raw.githubusercontent.com/ukairia777/tensorflow-nlp-tutorial/main/06.%20Machine%20Learning/dataset/Iris.csv", filename="Iris.csv")
data = pd.read_csv('Iris.csv', encoding='latin1')
print('샘플의 개수 :', len(data))
print(data[:5])# 중복을 허용하지 않고, 있는 데이터의 모든 종류를 출력
print("품종 종류:", data["Species"].unique(), sep="\n")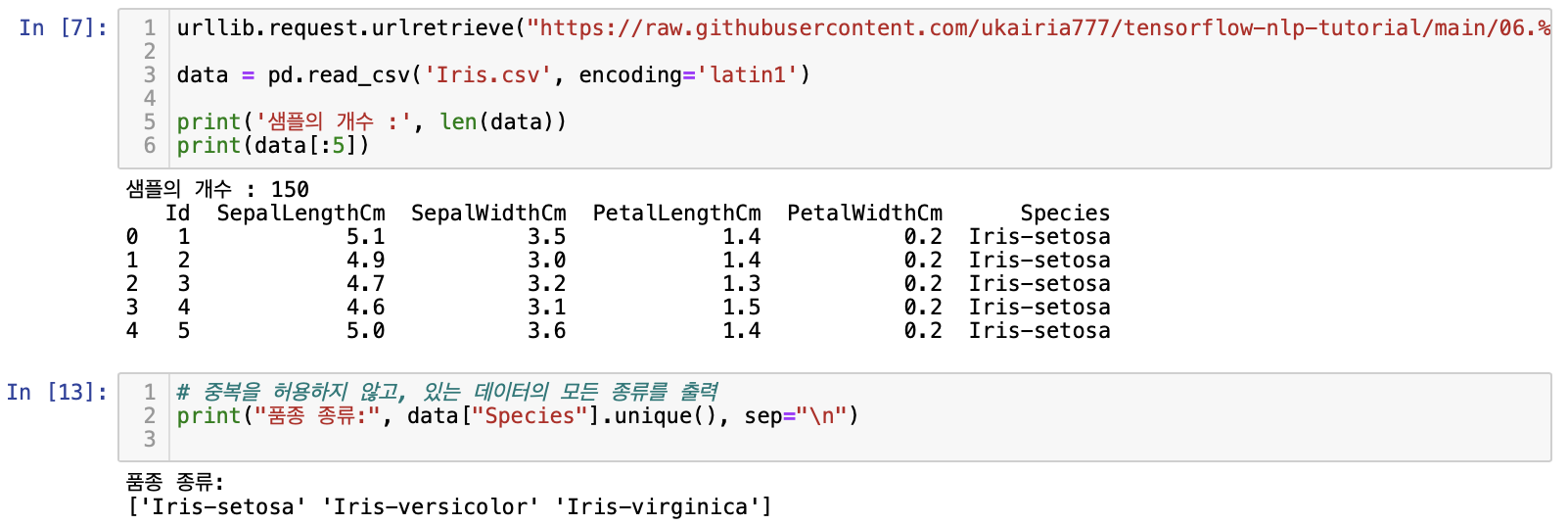
seaborn으로 시각화
sns.set(style="ticks", color_codes=True)
g = sns.pairplot(data, hue="Species", palette="husl")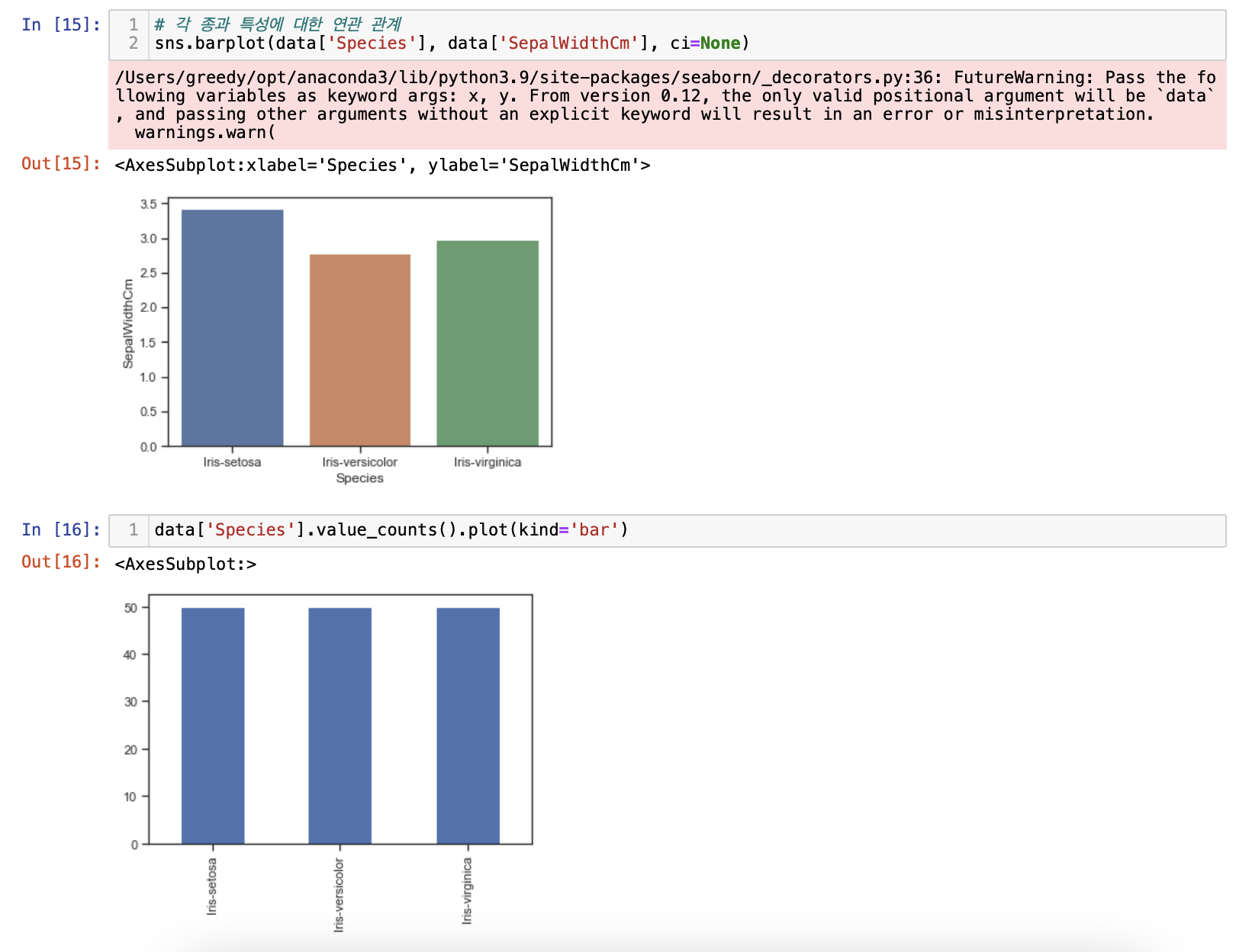
# 각 종과 특성에 대한 연관 관계
sns.barplot(data['Species'], data['SepalWidthCm'], ci=None)
# 분포 확인
data['Species'].value_counts().plot(kind='bar')
# Iris-virginica는 0, Iris-setosa는 1, Iris-versicolor는 2가 됨.
data['Species'] = data['Species'].replace(['Iris-virginica','Iris-setosa','Iris-versicolor'],[0,1,2])
data['Species'].value_counts().plot(kind='bar')# X 데이터. 특성은 총 4개.
data_X = data[['SepalLengthCm', 'SepalWidthCm', 'PetalLengthCm', 'PetalWidthCm']].values
# Y 데이터. 예측 대상.
data_y = data['Species'].values
print(data_X[:5])
print(data_y[:5])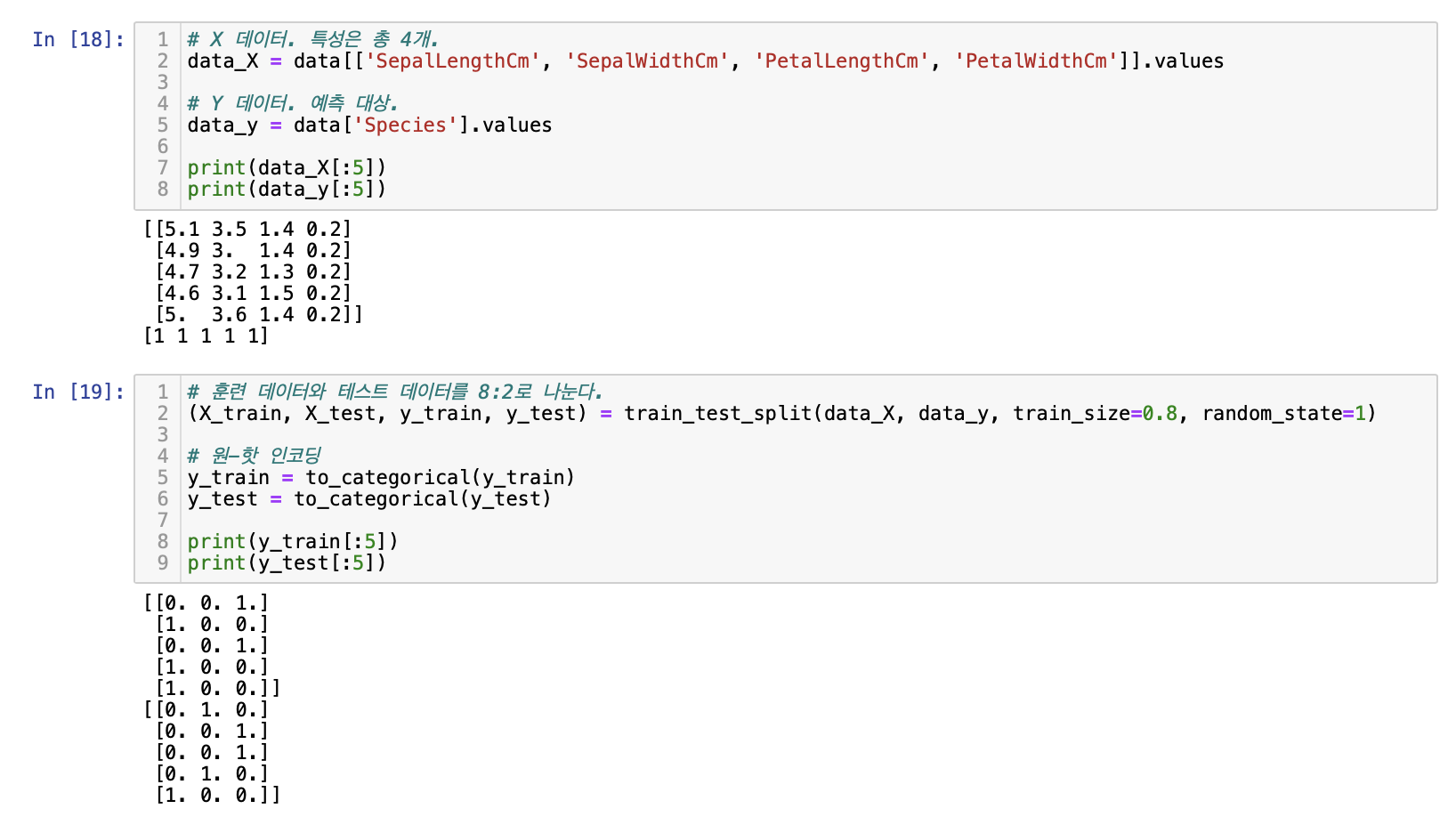
훈련 데이터와 테스트 데이터 분리, 원-핫 인코딩
--> 전처리 끝
소프트맥스 회귀
입력 차원4 = input_dim : 4
출력 3이므로 input_dim 앞 인자 3
activation = softmax
cost는 crossentropy
옵티마이저는 adam(경사하강법의 일종)
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
model = Sequential()
model.add(Dense(3, input_dim=4, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
history = model.fit(X_train, y_train, epochs=200, batch_size=1, validation_data=(X_test, y_test))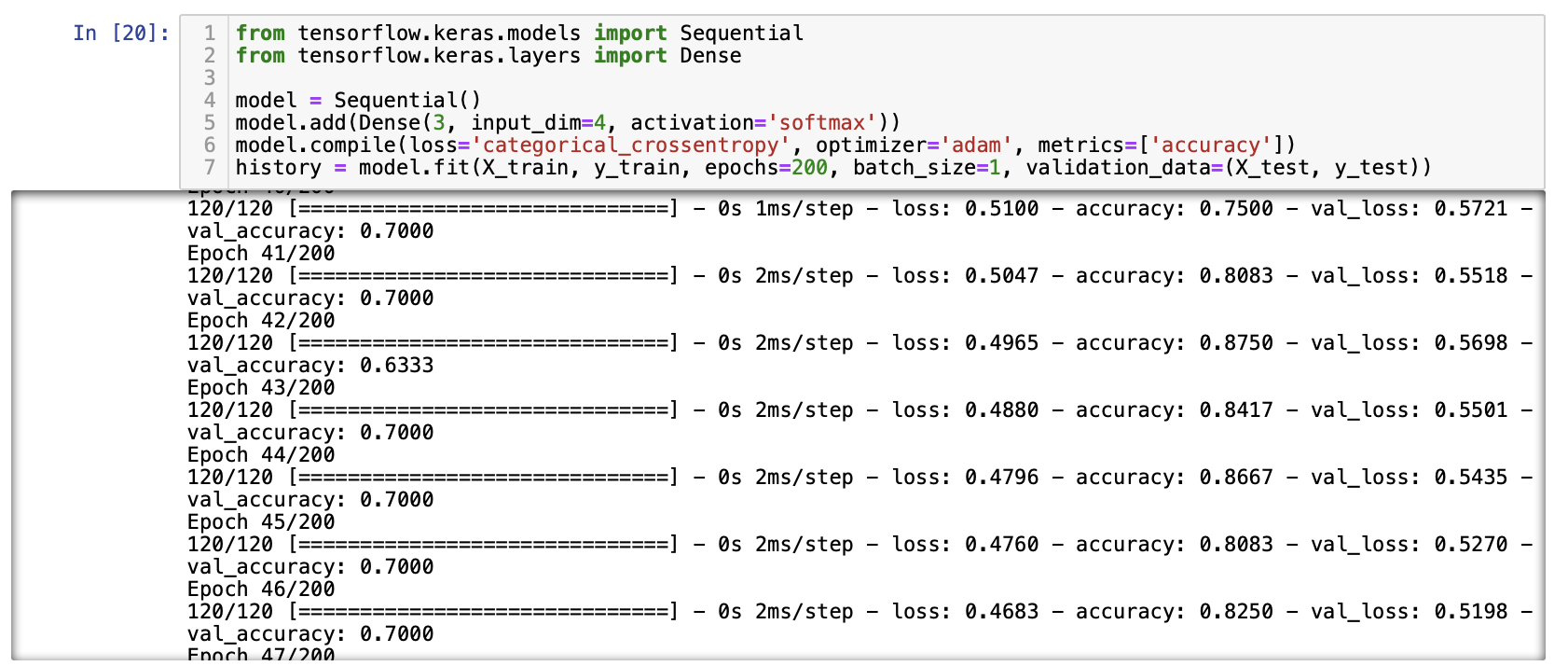
epochs = range(1, len(history.history['accuracy']) + 1)
plt.plot(epochs, history.history['loss'])
plt.plot(epochs, history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()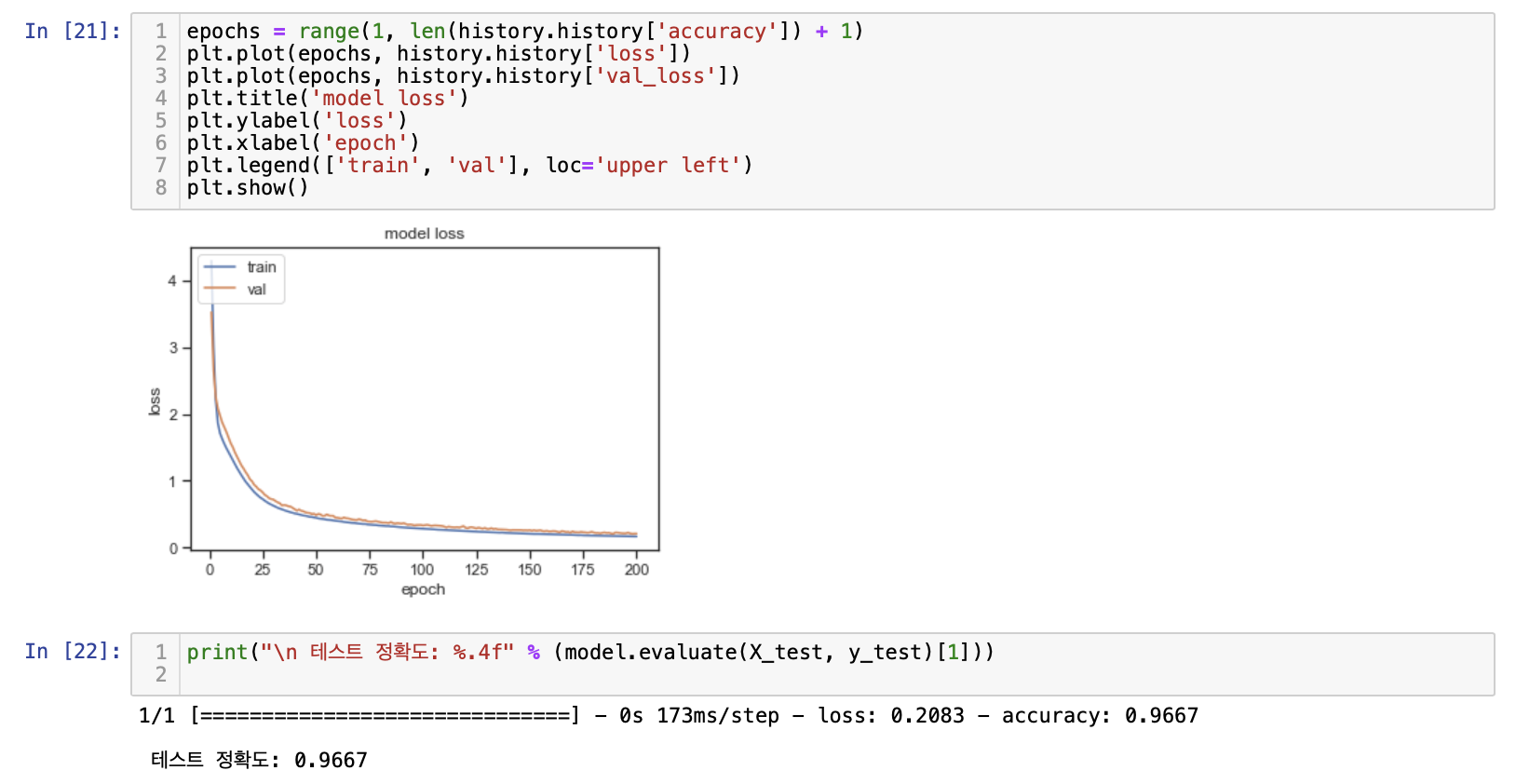
accuracy는 훈련 데이터의 정확도
val_accuracy는 테스트 데이터의 정확도
evaluate로 정확도 출력
print("\n 테스트 정확도: %.4f" % (model.evaluate(X_test, y_test)[1]))
테스트 정확도: 0.9667학습 출처 : https://wikidocs.net/35821
