🔴 신경망이란?
- 가중치 매개변수의 적절한 값을 데이터로부터 자동으로 학습하는 능력
🔴 신경망의 예시
- 입력층(0), 은닉층(1), 출력층(2)
- 신경망은 모두 3층으로 구성됨
- 가중치를 갖는 층은 2개 뿐이기 때문에 '2층 신경망'이라고 함
🔴 퍼셉트론 복습
- 퍼셉트론은 x1과 x2라는 두 신호를 입력받아 y를 출력하는 것을 의미
- b는 편향을 나타내는 매개변수로, 뉴런이 얼마나 쉽게 활성화되느냐를 제어함
- w1, w2는 각 신호의 가중치를 나타내는 매개변수로, 신호의 영향력을 제어함
🟠 활성화 함수
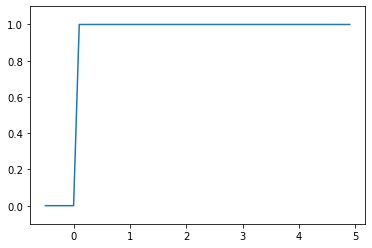
- 임계값을 경계로 출력이 바뀌는데, 이런 함수를 계단 함수라고 함
- 임계값을 경계로 출력이 바뀌는데, 이런 함수를 계단 함수라고 함
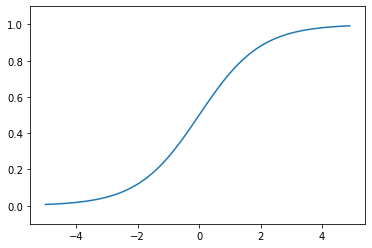
🟠 시그모이드 함수
- 함수는 입력을 주면 출력을 돌려주는 변화기와 같은 것
🟠 계단 함수 구현하기
# 인수 x는 실수(부동수소점)만 받아들임 def step_function(x): if x > 0: return 1 else: return 0# 넘파이 배열도 지원하게 수정 def step_function(x): y = x > 0 return y.astype(np.int)import numpy as np x = np.array([-1.0, 1.0, 2.0]) print(x) # [-1. 1. 2.] y = x > 0 # y는 bool배열 # 결과 [False True True] print(y)# y는 bool배열 --> int로 (수정) y = y.astype(np.int) y # 결과 array([0, 1, 1])
🟠 계단 함수 그래프
import numpy as np import matplotlib.pylab as plt def step_function(x): return np.array(x > 0, dtype=np.int) x = np.arange(-0.5, 5.0, 0.1) # -5.0 ~ 5.0 전까지 0.1 간격의 넘파이 배열을 생성 y = step_function(x) # step_function은 인수로 받은 넘파이 배열의 원소를 각각을 인수로 계단 함수 실행하여 # 그 결과를 다시 배열로 만들어 돌려줌 plt.plot(x,y) plt.ylim(-0.1, 1.1) # y축의 범위 지정 plt.show()
🟠 시그모이드 함수 구현하기
import numpy as np # np.exp(-x)는 exp(-x) 수식에 해당됨 def sigmoid(x): return 1 / (1 + np.exp(-x))x = np.array([-1.0, 1.0, 2.0]) sigmoid(x) # array([0.26894142, 0.73105858, 0.88079708])t = np.array([1.0, 2.0, 3.0]) print(1.0 + t) # [2. 3. 4.] print(1.0 / t) # [1. 0.5 0.33333333]import matplotlib.pylab as plt x = np.arange(-5.0, 5.0, 0.1) y = sigmoid(x) plt.plot(x, y) plt.ylim(-0.1, 1.1) # y축 범위 지정 plt.show
🟠 시그모이드 함수와 계단 함수 비교
- 계단 함수와 시그모이드 함수는 입력이 중요하면 큰 값을 출력함
- 입력이 중요하지 않으면, 작은 값을 출력함
- 입력이 아무리 작거나 커도 출력은 0~1 사이임
🟠 비선형 함수
- 계단함수와 시그모이드 함수의 공통점은 '비선형 함수' 라는 것임
- 시그모이드 함수는 곡선
- 계단 함수는 계단처럼 구부러진 직선으로 나타남과 동시에 비선형 함수로 분류됨
🟠 ReLU 함수
- ReLU는 입력이 0을 넘으면 그 입력을 그대로 출력하고, 0 이하이면, 0을 출력하는 함수임
# maximum은 두 입력 중 큰 값을 선택해 반환하는 함수임 def relu(x): return np.maximum(0, x)
🟢 다차원 배열의 계산
- 다차원 배열
import numpy as np A = np.array([1, 2, 3, 4]) print(A) # [1 2 3 4] np.ndim(A) A.shape A.shape[0] # 4B = np.array([[1,2], [3,4], [5,6]]) print(B) # [[1 2] [3 4] [5 6]] np.ndim(B) B.shape # (3, 2)
🟢 행렬의 곱
# 두 행렬의 곱은 넘파이 np.dot()으로 계산함 # np.dot()은 입력이 1차원 배열이면 벡터를, 2차원 배열이면 행렬 곱을 계산함 A = np.array([[1,2], [3,4]]) A.shape B = np.array([[5,6], [7,8]]) B.shape np.dot(A, B) # array([[19, 22],[43, 50]])# 2 x 3 행렬 A = np.array([[1,2,3], [4,5,6]]) A.shape # 3 x 2 행렬 B = np.array([[1,2], [3,4], [5,6]]) B.shape np.dot(A, B) # array([[22, 28],[49, 64]])C = np.array([[1,2], [3,4]]) C.shape A.shape np.dot(A, C)A = np.array([[1,2], [3,4], [5,6]]) A.shape B = np.array([7,8]) B.shape np.dot(A, B) # array([23, 53, 83])
🟢 신경망에서의 행렬 곱
X = np.array([1,2]) X.shape W = np.array([[1,3,5], [2,4,6]]) print(W) # [[1 3 5] [2 4 6]] W.shape Y = np.dot(X, W) print(Y) # [ 5 11 17]
🔵 3층 신경망 구현하기
- 3층 신경망 : 입력층(0층)은 2개, 첫 은닉층(1층)은 3개, 두번째 은닉층(2층)은 2개, 출력층(3층)은 2개의 뉴런으로 구성됨
🔵 표기법 설명
- 신경망에서의 계산을 행렬 계산으로 정리할 수 있음
🔵 각 층의 신호 전달 구현하기
X = np.array([1.0, 0.5]) W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]]) B1 = np.array([0.1, 0.2, 0.3]) print(W1.shape) # (2, 3) print(X.shape) # (2,) print(B1.shape) # (3,) # sigmoid() 함수는 넘파이 배열을 받아 같은 수의 원소로 구성된 넘파이 배열을 반환 A1 = np.dot(X, W1) + B1 Z1 = sigmoid(A1) print(A1) # [0.3, 0.7, 1.1] print(Z1) # [0.57444252, 0.66818777, 0.75026011]W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]]) B2 = np.array([0.1, 0.2]) print(Z1.shape) # (3,) print(W2.shape) # (3, 2) print(B2.shape) # (2,) A2 = np.dot(Z1, W2) + B2 Z2 = sigmoid(A2)# 항등 함수는 identify_function()을 정의하고, 이를 출력층의 활성화 함수로 이용했음 # 항등 함수는 입력을 그대로 출력하는 함수임 def identify_function(x): return x W3 = np.array([[0.1, 0.3], [0.2, 0.4]]) B3 = np.array([0.1, 0.2]) A3 = np.dot(Z2, W3) + B3 Y = identify_function(A3) # 혹은 Y = A3
- 회귀 = 항등함수
- 2클래스 함수 = 시그모이드 함수
- 다중 클래스 분류 = 소프트맥스 함수
🔵 구현정리
def init_network(): network = {} network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]]) network['b1'] = np.array([0.1, 0.2, 0.3]) network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]]) network['b2'] = np.array([0.1, 0.2]) network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]]) network['b3'] = np.array([0.1, 0.2]) return network def forward(network, x): W1, W2, W3 = network['W1'], network['W2'], network['W3'] b1, b2, b3 = network['b1'], network['b2'], network['b3'] a1 = np.dot(x, W1) + b1 z1 = sigmoid(a1) a2 = np.dot(z1, W2) + b2 z2 = sigmoid(a2) a3 = np.dot(z2, W3) + b3 y = identify_function(a3) return y # init_network(), forward() 함수 정의 network = init_network() x = np.array([1.0, 0.5]) y = forward(network, x) print(y) # [0.31682708 0.69627909]
- init_network() 함수는 가중치와 편향을 초기화하고 이들을 딕셔너리 변수인 network에 저장함
- 이 딕셔너리 변수 network에는 각 층에 필요한 매개변수(가중치와 편향)을 저장함
- forward() 함수는 입력 신호를 출력을 변환하는 처리 과정을 모두 구현하고 있음
- 함수 이름 forward()하 한 것은 신호가 순방향(입력에서 출력 방향)으로 전달됨(순전파)을 알리기 위함
🟣 출력층 설계하기
- 신경망은 분류와 회귀 모두에 이용할 수 있음
- 기계학습 문제는 분류와 회귀로 나눈다
- 분류는 데이터가 어느 class에 속하느냐의 문제임
- 회귀는 입력 데이터에서 연속적인 수치를 예측하는 문제임
🟣 항등 함수와 소프트맥스 함수 구현하기
- 항등 함수는 입력을 그대로 출력함 (= 입력과 출력이 항상 같다는 뜻)
- 출력층에선 항등 함수를 사용하면 입력 신호가 그대로 출력 신호가 됨
import numpy as np a = np.array([0.3, 2.9, 4.0]) exp_a = np.exp(a) # 지수 함수 print(exp_a) # [ 1.34985881 18.17414537 54.59815003] sum_exp_a = np.sum(exp_a) # 지수 함수의 합 print(sum_exp_a) # 74.1221542101633 y = exp_a / sum_exp_a print(y) # [0.01821127 0.24519181 0.73659691]def softmax(a): exp_a = np.exp(a) sum_exp_a = np.sum(exp_a) y = exp_a / sum_exp_a return y
🟣 소프트맥스 함수 구현시 주의점
- softmax() 함수코드는 오버플로 문제가 있음
- 오버플로란? : 컴퓨터 수는 4바이트나 8바이트와 같이 크기가 유한한 데이터로 다룸, 표현할 수 있는 수의 범위가 한정되어 너무 큰 값은 표현할 수 없다는 문제가 발생함
# 소프트맥스는 어떤 정수를 더해든 빼든 결과는 바뀌지 않음 a = np.array([1010, 1000, 990]) np.exp(a) / np.sum(np.exp(a)) # 소프트맥스 함수의 계산 array([nan, nan, nan]) --> 제대로 계산 안됨 c = np.max(a) # c = 1010(최대값) a - c # array([ 0, -10, -20]) np.exp(a - c) / np.sum(np.exp(a - c)) # array([9.99954600e-01, 4.53978686e-05, 2.06106005e-09])def softmax(a): c = np.max(a) exp_a = np.exp(a - c) # 오버플로 대책 sum_exp_a = np.sum(exp_a) y = exp_a / sum_exp_a return y
🟣 소프트맥스 함수의 특징
- 소프트맥스 함수의 출력은 0 ~ 1.0 사이의 실수임
- 소프트맥스 함수 출력의 총합은 1 (= 확률)
a = np.array([0.3, 2.9, 4.0]) y = softmax(a) print(y) # [0.01821127 0.24519181 0.73659691] np.sum(y) # 1.0
🟣 출력층의 뉴런 수 정하기
- 입력 이미지를 숫자 0 ~ 9 중 하나로 분류
🟤 손글씨 숫자 인식
- 먼저 훈련(학습)데이터를 사용해 가중치 매개변수를 학습하고, 추론 단계에서는 앞서 학습한 매개변수를 사용하여 입력 데이터를 분류함
🟤 MNIST 데이터 셋
- 입력 이미지를 숫자 0 ~ 9 중 하나로 분류
- 훈련이미지 60,000장, 시험이미지 10,000장
- 이미지 데이터 28 X 28 크기의 회색조 1채널
각 픽셀 0 ~ 255- ® 데이터 받는 주소 링크 : https://github.com/WegraLee/deep-learning-from-scratch
import sys, os sys.path.append(os.pardir) # 부모 디렉토리의 파일을 가져올 수 있도록 설정 from dataset.mnist import load_mnist # 처음 한 번은 몇분정도 시간걸림 (x_train, t_train), (x_test, t_test) = \ load_mnist(flatten=True, normalize=False) # 각 데이터의 형상 출력 print(x_train.shape) # (60000, 784) print(t_train.shape) # (60000, ) print(x_test.shape) # (10000, 784) print(t_test.shape) # (10000, )
- load_mnist 함수는 읽은 MNIST 데이터를 (훈련 이미지, 훈련 레이블), (시험 이미지, 시험 레이블) 형식으로 반환
- 인수로는 normalize,, flatten, one_hot_label 세 가지를 설정할 수 있음
- 세 인수 모두 bool 값임
- 첫번째 인수 normalize는 입력 이미지의 픽셀 값을 0.0 ~ 1.0 사이의 값으로 정규화 할지를 정함
- False로 설정하면, 입력 이미지를 1 x 28 x 28의 3차원 배열로, True로 설정하면 784개의 원소로 이뤄진 1차원 배열로 저장함
- 세번째 인수 one_hot_lavel은 레이블을 원-핫-인코딩 형태로 저장할지 정함
- 원-핫-인코딩은 정답을 뜻하는 원소만 1이고, 나머지는 모두 0인 배열을 의미
- 파이썬에는 pickle(피클)이라는 편리한 기능이 있음
- 이는 프로그램 실행 중에 특정 객체를 파일로 저장하는 기능임
- 저장해둔 pickle 파일을 로드하면, 실행 당시의 객체를 즉시 복원할 수 있음
- MNIST 데이터셋을 읽는 load_mnist() 함수에서도 2번째 이후의 읽기 시, pickle를 이용함
- pickle 덕분에 MNIST 데이터를 순식간에 준비할 수 있음
import sys, os sys.path.append(os.pardir) import numpy as np from dataset.mnist import load_mnist from PIL import Image def img_show(img): pil_img = Image.fromarray(np.uint8(img)) pil_img.show() (x_train, t_train), (x_test, t_test) = \ load_mnist(flatten=True, normalize=False) img = x_train[0] label = t_train[0] print(label) # 5 print(img.shape) # (784,) img = img.reshape(28, 28) # 원래 이미지의 모양으로 변형 print(img.shape) # (28, 28) img_show(img)
- flatten=True로 설정해 읽어드린 이미지는 1차원 넘파이 배열로 저장되어 있음
- 이미지를 표시할 때, 원래 형상인 28 x 28 크기로 다시 변형해야 함
- reshape() 메서드는 원하는 형상을 인수로 지정하면 넘파이 배열의 형상을 바꿀 수 있음
- 넘파이로 저장된 이미지 데이터를 PIL용 데이터 객체로 변환해야하며, 이 변환은 Image.fromarray()가 수행함
🟤 신경망의 추론 처리
- MNIST, 이 신경망은 입력층 뉴런을 784개, 출력층 뉴런을 10개로 구성함
- 입력층 뉴런이 754개인 이유는 이미지 크기가 28 X 28 = 784 이기 때문
- 출력층 뉴런이 10개인 이유는 0 ~ 9까지의 숫자를 구분하는 문제이기 때문
import pickle import numpy as np def sigmoid(x): return (1 / (1 + np.exp(-x))) def get_data(): (x_train, t_train), (x_test, t_test) = \ load_mnist(normalize=True, flatten=True, one_hot_label=False) # normalize=True는 0 ~ 255 범위인 각 픽셀의 값을 0.0 ~ 1.0 범위로 변환 # 데이터를 특정 범위로 변환하는 처리를 정규화(normalize)라고 함 # 신경망의 입력 데이터에 특정 변환을 가하는 것 --> 전처리(pre-procssing) # 입력 이미지 데이터에 대한 전처리 작업으로 정규화 시킴 return x_test, t_test def init_network(): with open("C:/Users/yuri/AI_master/밑바닥부터 시작하는 딥러닝1/deep-learning-from-scratch/ch03/sample_weight.pkl", 'rb') as f: network = pickle.load(f) return network def predict(network, x): W1, W2, W3 = network['W1'], network['W2'], network['W3'] b1, b2, b3 = network['b1'], network['b2'], network['b3'] a1 = np.dot(x, W1) + b1 z1 = sigmoid(a1) a2 = np.dot(z1, W2) + b2 z2 = sigmoid(a2) a3 = np.dot(z2, W3) + b3 y = softmax(a3) return y
- 전처리를 통해 식별 능력을 개선하고 학습 속도를 높임
- 위의 예시는 각 픽셀의 값을 255로 나누는 단순한 정규화를 수행하였지만, 데이터 전체의 분포를 고려해 전처리하는 경우가 많음
- ex) 데이터 전체 평균과 표준편차를 이용하여 데이터들이 O을 중심으로 분포하도록 이동하거나 데이터의 확산 범위를 제한하는 정규화를 수행함
- 그 외에도 전체 데이터를 균일하게 분포시키는 데이터 백색화가 있음
# 정확도 평가 x, t = get_data() network = init_network() accuracy_cnt = 0 for i in range(len(x)): y = predict(network, x[i]) p = np.argmax(y) # 확률이 가장 높은 원소의 인덱스를 얻음 if p == t[i]: accuracy_cnt += 1 print("Accuracy:" + str(float(accuracy_cnt) / len(x))) # Accuracy:0.9352 --> 올바르게 분류할 비율이 93.52%
- 세가지 함수를 사용해 신경망에 의한 추론 수행, 정확도 평가
- for문을 돌며 x에 저장된 이미지 데이터를 1장씩 꺼내 predict() 함수로 분류
- predict() 함수는 각 레이블의 확률을 넘파이 배열로 변환 (ex. 이미지가 숫자 '0'일 확률이 0.1)
- 그런 다음, np.argmax() 함수로 이 배열에서 값이 가장 큰(확률이 가장 높은) 원소의 인덱스룰 구함
- 마지막으로, 신경망이 예측한 답변과 정확 레이블을 비교하여 맞힌 숫자 accuracy_cnt를 세고, 이를 전체 이미지 숫자로 나눠 정확도를 구함
🟤 배치 처리
- 구현한 신경망 각 층의 가중치 형상을 출력
x, _ = get_data() network = init_network() W1, W2, W3 = network['W1'], network['W2'], network['W3'] x.shape # (10000, 784) x[0].shape # (784,) W1.shape # (784, 50) W2.shape # (50, 100) W3.shape # (100, 10)x, t = get_data() network = init_network() batch_size = 100 # 배치 크기 accuracy_cnt = 0 for i in range(0, len(x), batch_size): x_batch = x[i:i+batch_size] y_batch = predict(network, x_batch) p = np.argmax(y_batch, axis = 1) accuracy_cnt += np.sum(p == t[i:i+batch_size]) print("Accuracy:" + str(float(accuracy_cnt) / len(x))) # Accuracy:0.9352
- range()함수는 range(start, end) 처럼 인수를 2개 지정해 호출하면, start에서 end-1까지의 정수로 이뤄진 리스트를 반환함
- range(start, end, step)처럼 인수를 3개 지정하면, start ~ end-1까지 step 간격으로 증가하는 리스트를 반환함
list(range(0,10)) # [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] list(range(0,10,3)) # [0, 3, 6, 9]
- range() 함수가 반환하는 리스트를 바탕으로 x[i:i+batch_size]에서 입력 데이터를 묶음
- x[i:i+batch_size]는 입력 데이터의 i번째 부터 i+batch_size번째 까지의 데이터를 묶는다는 의미
- batch_size가 100 이므로, x[0:100], x[100:200]과 같이 앞에서부터 100장씩 묶어 꺼냄
- argmax()는 최댓값의 인덱스를 가져옴
- 여기서는 axis = 1을 추가하였는데, 이는 100 x 10 배열 중 1차원 배열을 구성하는 각 원소에서 최댓값의 인덱스를 찾도록 위함
x = np.array([[0.1, 0.8, 0.1], [1.3, 0.1, 0.6], [0.2, 0.5, 0.3], [0.8, 0.1, 0.1]]) y = np.argmax(x, axis=1) print(y) # [1 0 1 0]y = np.array([1, 2, 1, 0]) t = np.array([1, 2, 0, 0]) print(y == t) # [ True True False True] np.sum(y == t) # 3
⚪ 정리
- 신경망에서는 매끄럽게 변화하는 시그모이드 함수를 사용
- 퍼셉트론에서는 갑자기 변화하는 계단 함수를 사용
- 이 차이는 신경망 학습에 중요함
- 신경망에서는 활성화 함수로 시그모이드 함수와 ReLU 함수 같은 매끄럽게 변화하는 함수를 이용함
- 넘파이의 다차원 배열을 잘 사용하면, 신경망을 효율적으로 구현할 수 있음
- 기계학습 문제는 크게 회귀와 분류로 나눌 수 있음
- 출력층의 활성화 함수로는 회귀에서는 주로 항등 함수를, 분류에서는 주로 소프트맥스 함수를 사용함
- 분류에서는 출력층의 뉴런 수를 분류하려는 클래스 수와 같게 설정함
- 입력 데이터를 묶은 것을 배치라 하고, 추론 처리를 이 배치 단위로 진행하면 결과를 훨씬 빠르게 얻을 수 있음