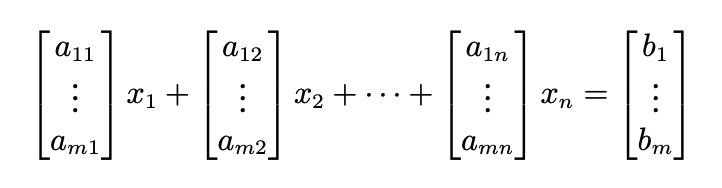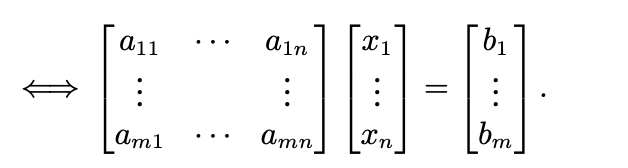이 시리즈는 Mathematics for Machine Learning의 내용을 번역 및 재해석해서 작성한 글입니다. 이 책의 내용에 이해를 돕는 글을 첨부하였으며 완전한 번역본이 아님을 알려드립니다.
2.1 Systems of Linear Equations
선형 방정식 시스템은 선형대수에서 중요한 역할을 합니다. 많은 문제들은 선형방정식 시스템으로 표현될 수 있고, 선형대수학을 통해 우리는 이 방정식을 풀 수 있습니다.
Exercise 2.1 연립방정식
회사에서 R1,R2,...,Rn−1,Rn의 자원을 필요로 하는 제품 N1,N2,...,Nn−1,Nn 라는 상품을 생산합니다. Nj를 생산하기 위해ㅔ서는 Ri의 자원이 요구됩니다. 이 때 요구하는 자원의 양은 aij가 됩니다.
문제는 최적의 생산 계획을 찾는 것이 목표이니, 자원 Ri의 총량 유닛을 bi 라고 가정한다면, 상품 Nj가 생산되는 개수 xj는 얼마나 될 수 있을까요?(모든자원은 사용가능하고, 남는 자원은 없다고 가정합니다.)
ai1x1 + ai2x2 + ainxn = bi
따라서 위 다항식은 각 상품의 개수 xi ~ xn를 생산할 때 드는 자원 Ri의 총량 유닛인 bi이라고 말할 수 있습니다.
그렇다면 자원 R1,R2,...,Rn−1,Rn 에 대해서는 다음과 같은 식이 정리됩니다.
a11x1 + a12x2 + a1nxn = b1
a21x1 + a22x2 + a2nxn = b2
⋮
am1x1 + am2x2 + amnxn = bm
위와 같은 식들을 연립방정식이라고 하고, 찾고 싶은 값인 x1,x2,...,xn−1,xn을 미지수라고 합니다. 이러한 식을 만족하는 x1,x2,...,xn−1,xn을 일차 연립방정식의 해라고 합니다.
해의 종류 : 3가지
1) 해가 없는 경우(0)
x1 + x2 + x3 = 3 (1)
x1 - x2 + x3 = 2 (2)
x1 + 3x3 = 1 (3)
2) 유일한 해가 존재하는 경우(1개)
x1 + x2 + x3 = 3 (1)
x1 - x2 + x3 = 2 (2)
x2 + 3x3 = 2 (3)
3) 해가 무수히 많은 경우
x1 + x2 + x3 = 3 (1)
x1 - x2 + x3 = 2 (2)
2x1 + 3x3 = 5 (3)
일반적으로, 연립방정식의 해는 위 3가지 중 1가지에 속합니다. Chap 9에서 배우는 선형 회귀(Linear Regression)에서 수 많은 방정식으로 만들어진 일차 연립방정식에서 유일한 해를 찾지 못할 때, 어떻게 해야하는 지 배울 수 있습니다.
연립방정식은 행렬식
일차 연립방정식을 다시 살펴봅니다. 우리가 관심 있는 것은 미지수인 x1,x2,...,xn−1,xn 입니다. 아래의 식에서
a11x1 + a12x2 + a1nxn = b1
a21x1 + a22x2 + a2nxn = b2
⋮
am1x1 + am2x2 + amnxn = bm
계수와 미지수를 분리하여 다음과 같이 표현할 수 있습니다.
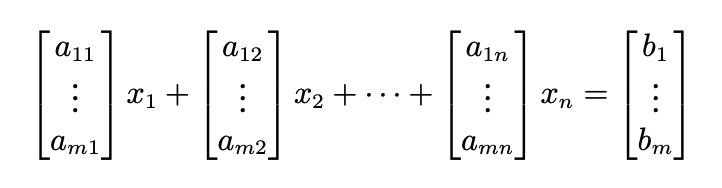
같은 계수를 행렬로, 미지수의 집합을 벡터로 표현한다면 아래처럼 행렬식으로 표현할 수 있습니다. 이 때, 아래의 형태를 compact notation라고 합니다.
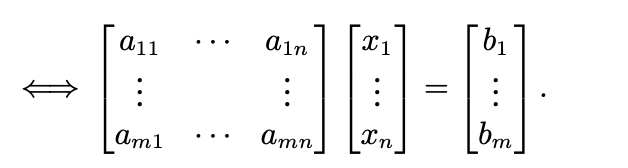
Contributor
Matt J
맹준영