#230329 수
매일매일 한 챕터씩 공부하는 건 참 좋은 것 같다. 정리가 좀 오래 걸려서 고작 20-30쪽 읽는데 몇 시간씩 걸리고 있긴 하지만 이러면 뭐라도 남겠지? 기억력이 너무 나빠서 이렇게라도 해야됨.. 미래의 내가 잊어버렸을 때마다 열어볼 수 있게.. 경작하면서 벨로그 쓰는 습관이 생긴 것은 참 좋은 것 같다. 집중력 저하될 때 벨로그 쓰면서 하면 강제로라도 집중하게 된다. 그리고 감정 기복 심할 때마다 뭐 어디 얘기할 곳도 없고 일기 쓰기는 귀찮고(작년에 다이어리 사서 일주일 써봄) 그랬는데 습관으로 자리잡고 나니 공부한 거랑 그날의 기분 tmi 다 때려부을 수 있어서 좋음
오늘의 주제는?
4장 분류하는 유닛을 만들어봅시다~ <이진 분류>
- 초기 인공지능 이진 분류 알고리즘(퍼셉트론, 아달린)
- 로지스틱 회귀란?
1. 초기 인공지능 알고리즘으로 로지스틱 회귀를 이해해 봅시다~
1) 기본 용어
퍼셉트론 : 1957년 코넬 항공 연구소의 프랑크 로젠블라트가 발표한, 이진 분류 문제에서 최적의 가중치를 학습하는 알고리즘
이진 분류 : 샘플 데이터를 true 혹은 false로 구분하는 문제
2) 퍼셉트론의 구조
퍼셉트론은 선형 회귀와 유사한 구조를 가지고 있다.
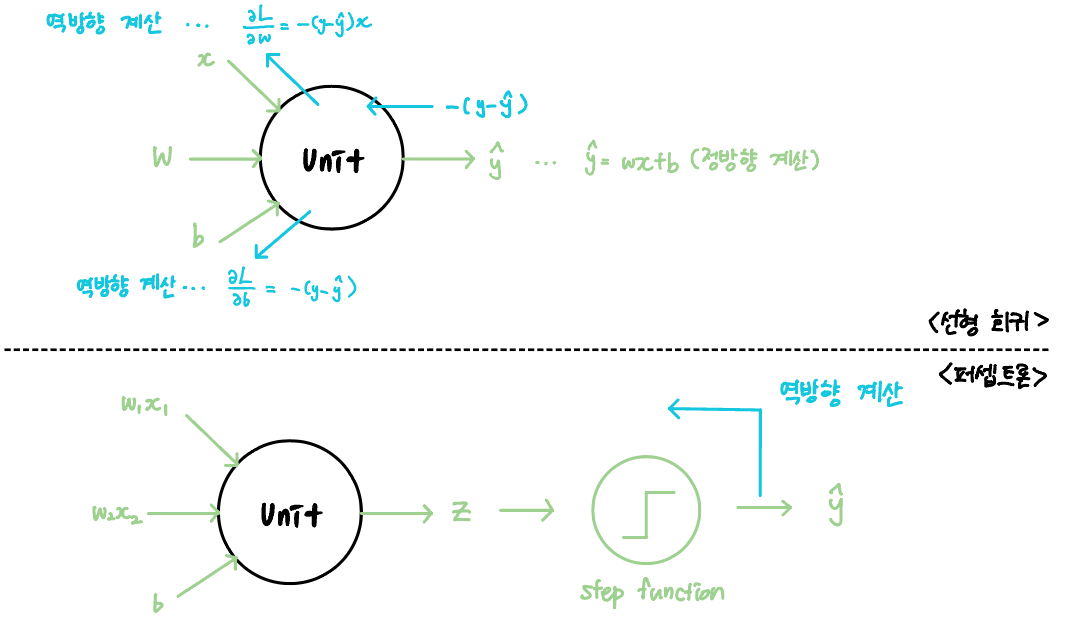
유사한 구조를 가지고 있다고 한 이유는 별 게 아니고 그냥 퍼셉트론도 선형회귀처럼 직선 방정식을 사용하기 때문이다.
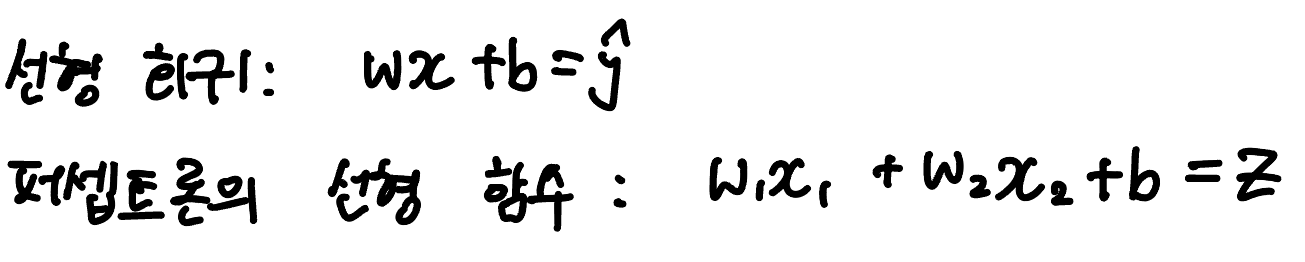
퍼셉트론의 유닛은 입력 신호들을 받아 위의 직선 방정식을 계산한 값 z를 만들고, z를 다시 계단함수에 통과시켜 예측값 ŷ를 구한다.
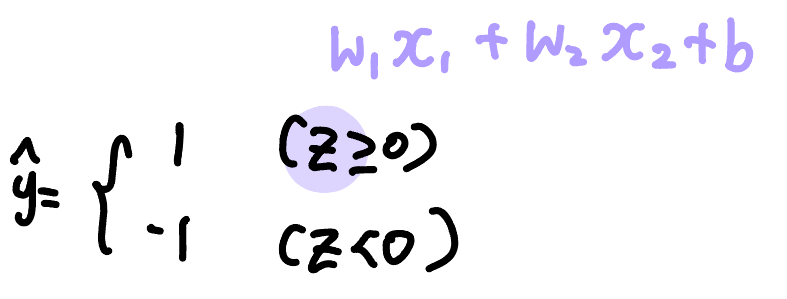
계단함수는 z가 0보다 크면 1로, 0보다 작으면 -1로 분류하기 때문에 ŷ는 1 또는 -1의 값을 갖게 된다. 그리고 계단함수의 결과를 사용하여 역방향 계산으로 가중치와 절편을 업데이트한다.
+) 1을 양성 클래스, -1을 음성 클래스라고 한다.
위에서 본 퍼셉트론의 선형 함수는 특성이 2개인 경우의 선형 함수이다. 하지만 실제 샘플들은 17일차 벨로그(3장)에서 살펴본 당뇨병 환자 데이터처럼 특성이 여러 개인 경우가 더 많다 (당뇨벙 환자 데이터에서는 10개였다). n개의 특성에 대한 선형함수는 다음과 같이 표기할 수 있다,
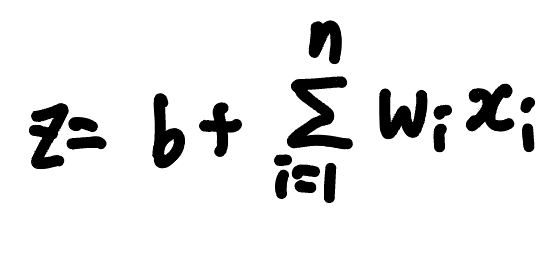
3) 아달린의 구조
아달린 : 1960년 스탠포드 대학의 버나드 위드로우와 테드 호프가 발표한, 퍼셉트론을 개선한 적응형 선형 뉴런
계단 함수의 결과를 가중치와 절편을 업데이트하는 데에 사용한 퍼셉트론과 달리, 아달린은 계단 함수의 결과는 ŷ를 구하는 예측에만 활용하고 가중치와 절편은 선형 함수의 결과로 업데이트 한다.
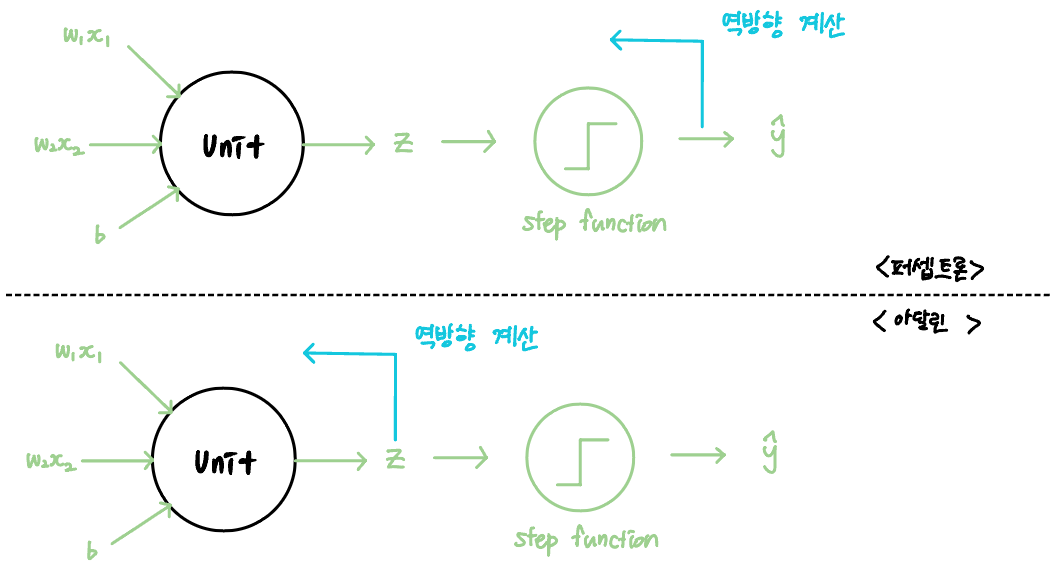
역방향 계산이 선형 함수 출력 이후에 일어난다는 점 외에 퍼셉트론과 아달린의 차이는 없으므로, 다음 내용으로 넘어가자.
4) 로지스틱 회귀의 구조
로지스틱 회귀는 아달린에서 조금 더 발전한 형태의 알고리즘이다.
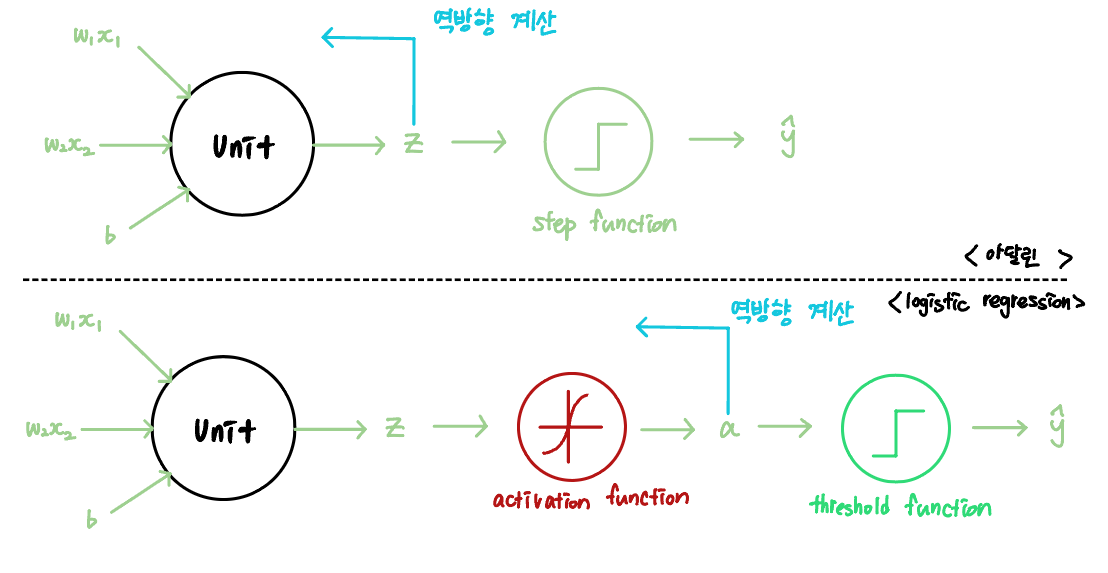
입력 신호들을 선형 함수에 통과시켜 얻은 z를 임계 함수에 보내기 전, 활성화 함수를 이용해 변형시킨다. 임계 함수는 퍼셉트론과 아달린의 계단 함수와 역할은 유사하지만, 계단 함수는 선형 함수의 출력값z를, 임계 함수는 활성화 함수의 출력값 a를 사용한다는 점에서 다르다.
전부 이해한 것 같지만 아직 모르는 게 한 가지있다. 활성화 함수는 대체 뭔가요..? 활성화 함수는 주로 비선형 함수가 사용된다. 예를 들어,
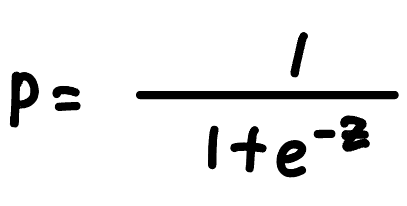
이런 식으로.. 생겼다.
왜 비선형 함수일까? 만약 활성화 함수가 z에 대한 선형함수라면
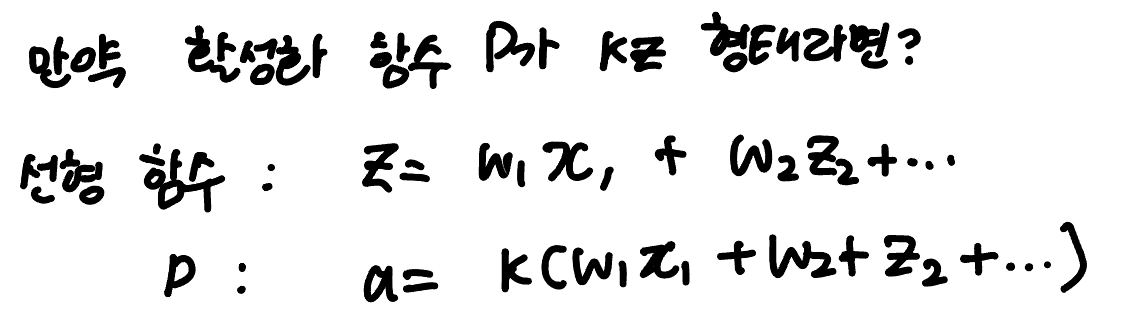
z값이나 a값이나 상수 k가 곱해진 것 빼곤 별 차이가 없는데 뭣하러 통과시키겠습니까? 그냥 아달린과 다를 게 없다. 활성화 함수가 필요하지도 않을 것이다. 그러면 활성화 함수는 대체 왜 필요하냐! 얜 하는 일이 뭐냐! 하는 일이 있으니 이렇게 비선형 함수로 만든 것 아니냐! 그것에 대해 알아보자. 어떻게? 로지스틱 회귀의 활성화 함수인 '시그모이드 함수'를 통해서!
2. 시그모이드 함수로 확률을 만들어보자
1) 시그모이드 함수의 역할
시그모이드 함수는 z를 0~1 사이의 확률값 a로 변환시켜주는 역할을 한다. 예를 들어 시그모이드 함수를 통과한 a값이 0.7이고 사용된 샘플 데이터가 암 종양 판정이라면 0.7은 양성 샘플일 확률(환자가 악성 종양일 확률)로 해석할 수 있다. 0.5를 넘기면 양성 클래스, 0.5 이하면 음성 클래스로 분류하는 경우가 많다. (퍼셉트론과 아달린에서는 계단 함수를 통과한 ŷ가 1이면 양성, -1이면 음성으로 분류하였다.)
2) 시그모이드 함수가 만들어지는 과정
역할을 알아봤으니 이제 어떻게 생겼는지도 알아야 할 것이다.
시그모이드 함수는 odds ratio라는 통계를 기반으로 만들어진다.
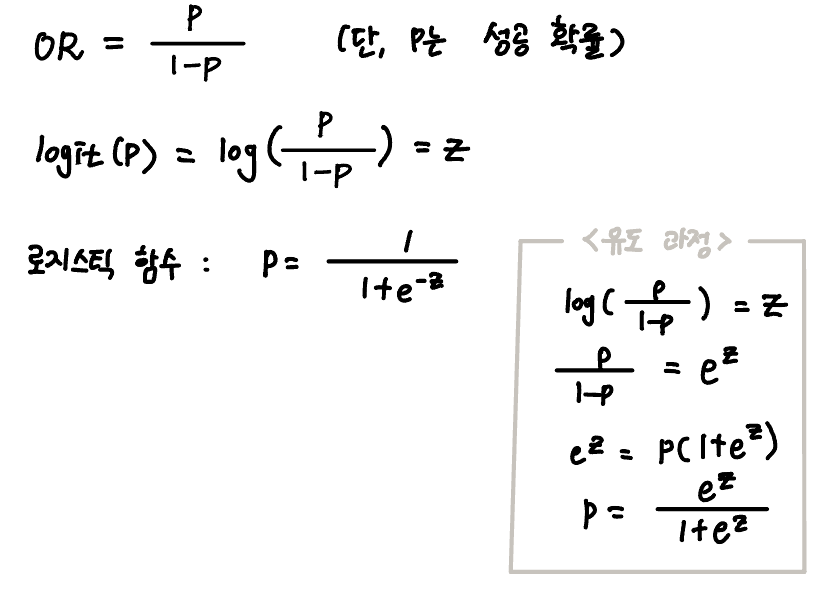
OR은 odds ratio,
logit(p)는 오즈 비에 자연 로그 함수를 취해 만든 로짓 함수,
로지스틱 함수는 로짓 함수를 z에 대해 정리한 것이다. z에 대해 정리하는 이유는 z를 가로축에 놓기 위함이다.
오즈비, 로짓 함수, 로지스틱 함수를 각각 그래프에 그리면 다음과 같이 생겼다.
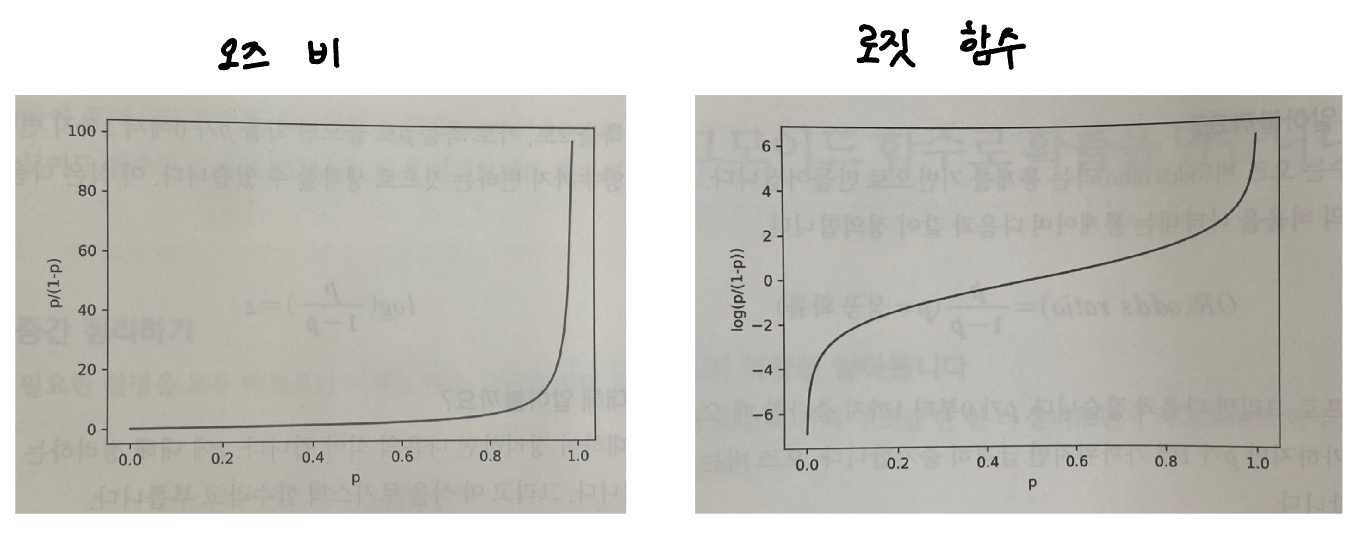
로짓 함수의 가로와 세로 축을 뒤집으면,
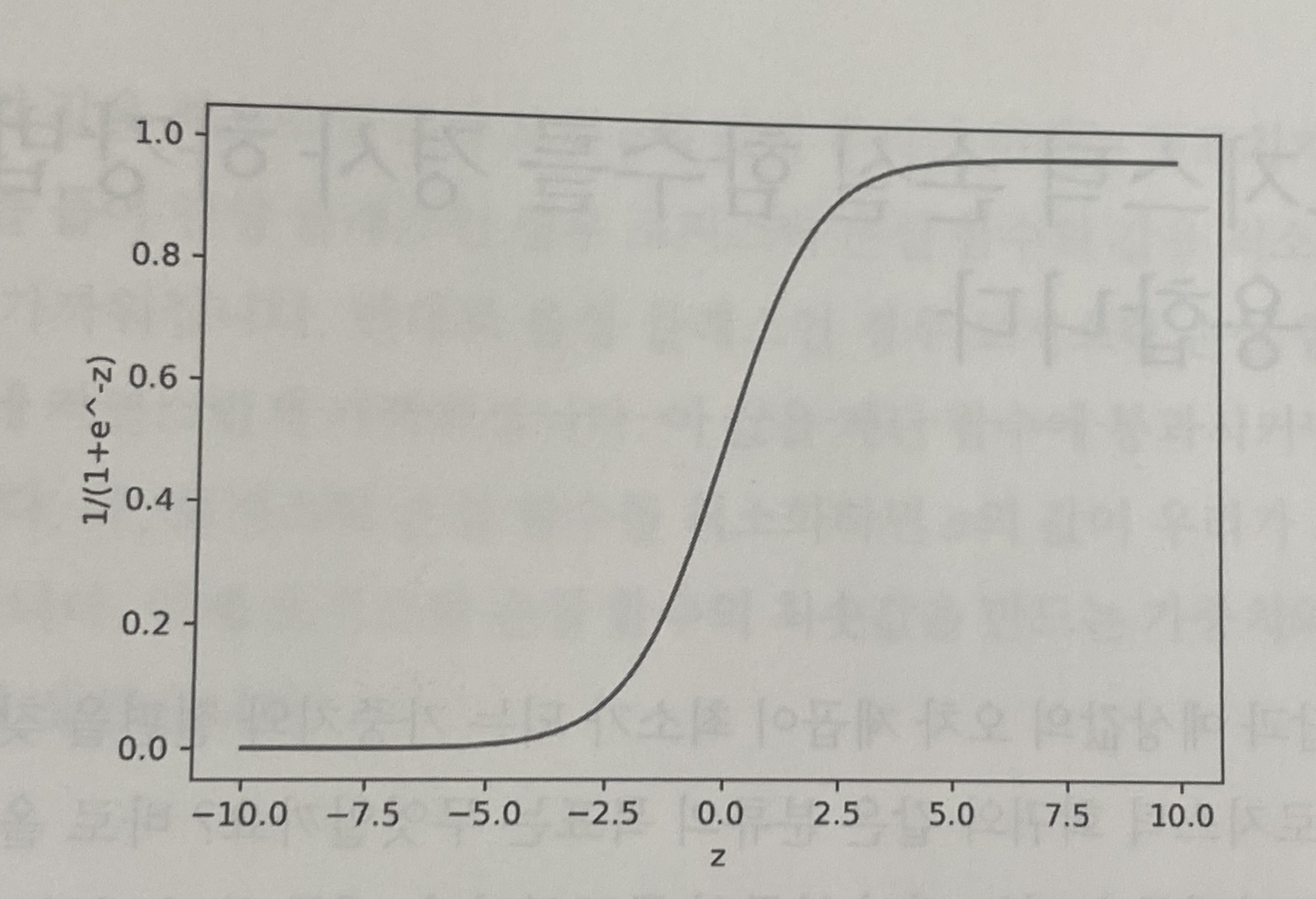
짜란~ 로지스틱 함수! 모양 때문에 로지스틱 함수를 시그모이드 함수라고 한다.
3) 시그모이드 함수 파고들기
