#230320 월
1. 강화학습의 개념들
- neural network : reinforcement learning framework 중 하나
- deep neural network를 사용한 rl이 deep learning
- deep learning은 agent가 어떻게 작동하도록 할 것인지 안내해주는 agent의 알고리즘이라고도 할 수 있음
2. 강화학습의 이론들
1) multi-armed bandit problem
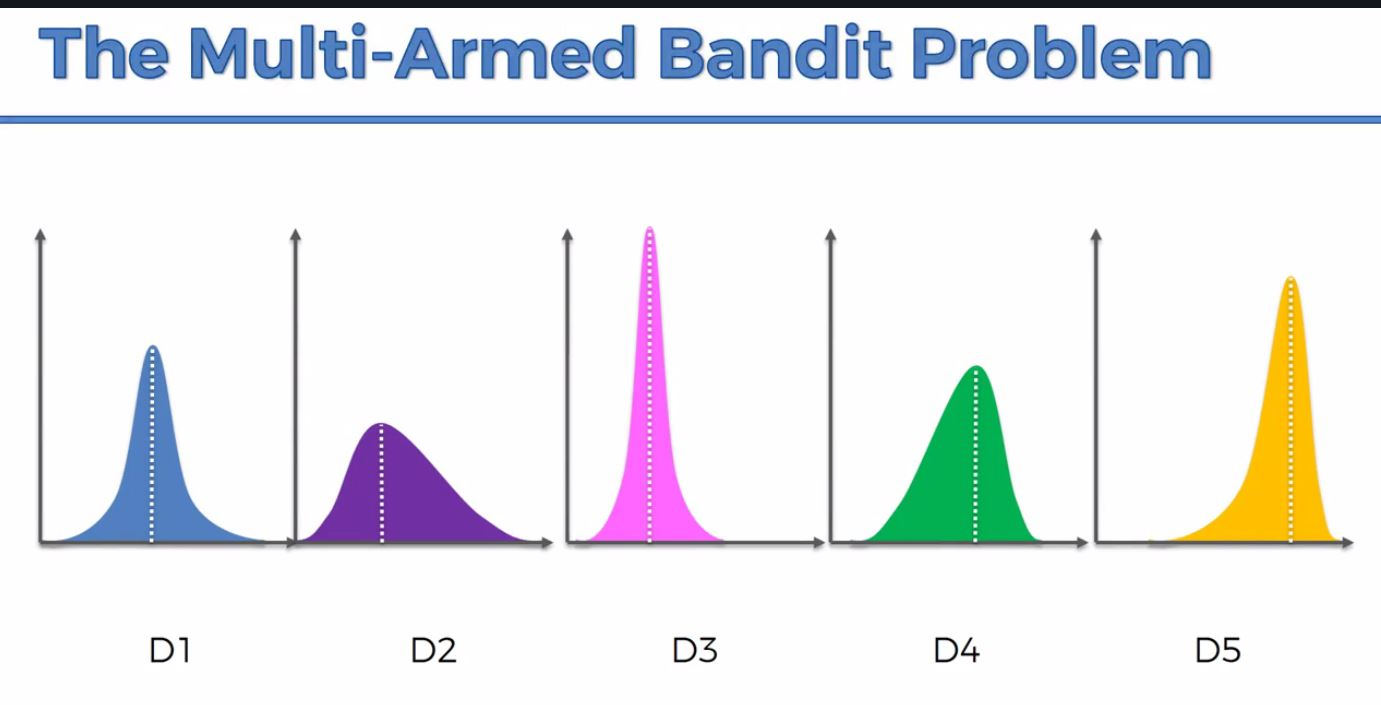slot machine이 모두 분포가 다름 = mean, 표준편차가 다름
-> 어떤 전략을 써야 reward를 maximize 할 수 있을까?
- epsilon-greedy policy : 추정되는 가장 큰 reward를 매번 선택하는 전략
- argmax policy : 가장 큰 predicted probablity를 가진 클래스를 찾는 전략
2) state, action, reward
현재 state에서 어떤 action을 취하면 얼마만큼의 reward가 있는가?
3) Markov Decision Process
의사결정 과정을 모델링하는 것
모든 문제는 MDP 문제로 바꿀 수 있음
그리고 이 MDP 문제는 RL로 풀 수 있음
4) value function
input은 변동 가능한 state
policy는 고정
-
state value function은 given state에서의 G_t 기댓값 리턴
-
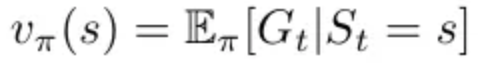
action value function은 policy π에서 agent가 어떤 action a를 취했을 때 나오는 기댓값 리턴
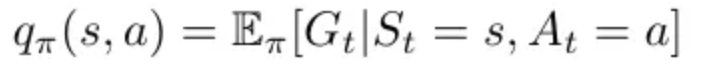
=> 어떤 state가 가장 가치가 높은지(reward를 maximize 해주는지)를 알 수 있음
5) policy function
policy 고정 x
policy, state가 모두 input -> 어떤 확률로 어떤 action을 취할지를 return 해줌
=> 해당 state에서 어떤 action이 가장 좋은지를 알 수 있음
6) state value
어떤 state를 starting point로 잡았을 때의 overall reward의 예측 기댓값
7) sparse reward problem
ex) 체스는 게임이 끝나기 전까지는 해당 state가 적절한지 아닌지(reward를 얼마를 줘야할지) 전혀 알 수 없음
-> 게임이 끝나기 직전의 마지막 수에만 reward를 줄 수 있음
= environment는 거대한데 그에 비해 reward는 부족함
8) Q-learning
4)의 value function과 거의 같은 개념이다. goal에 가까운 state일수록 높은 reward를 반영하여, 머신이 가치가 높은 state로 다가가도록 함. for loop를 돌면서 머신은 점점 Q-value를 찾아나감. 그래서 7)의 sparse reward problem을 어느정도 해결할 수 있다.
9) tensor
real world의 environment를 컴퓨터가 계산할 수 있는 n차원 배열(n>2)로 표현하기 -> 이 tensor가 input이 됨
10) credit assignment
- 7)에서 말했듯 강화학습에서는 sparse reward problem이 존재한다. 그러면 게임이 끝난 후 이전까지의 모든 수에 어떻게 credit을 분배할까? 주로 goal에 가까운 state일수록 크게, 멀어질수록 낮게 주는 reward descent를 사용한다.
3. 강화학습 방법 : neural network를 얼마나 자주 update하느냐로 분류 가능
1) Monte Carlo Learning
random sampling 반복
2) online learning
3) actor-critic
state function이 예측한 state value vs action function이 보여주는 reward -> 예상했던 reward만큼을 받았는가 아닌가를 평가하며 학습하는 방법
