BOJ 2193 이친수

어떤 문제가 최적 부분 구조와 부분 문제 반복을 만족하는 경우, dp를 적용해 풀 수 있다.

2193번 역시 두 조건을 만족하므로 dp를 이용해 풀어보았다.

풀이:

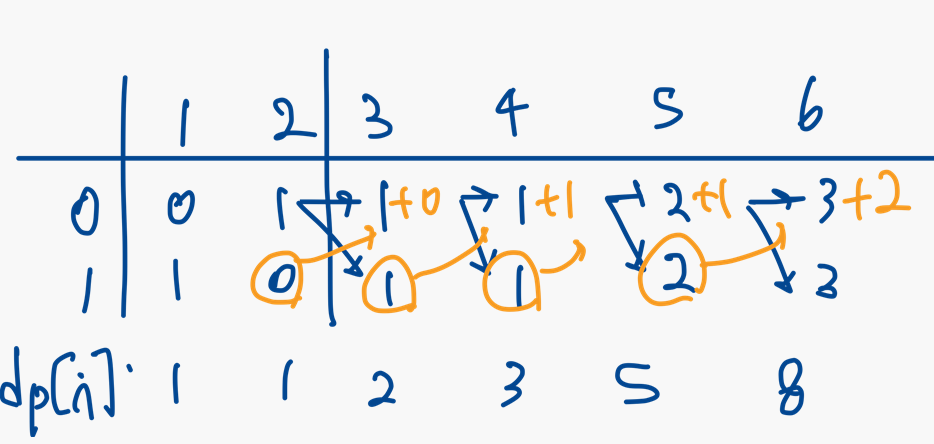
dp[0]=1, dp[1]=1 일때,
관찰을 통해 점화식이 dp[n]=dp[n-1]=dp[n-2] 라는 것을 알 수 있다.

결과적으로 점화식이 피보나치 수열과 동일한 형태라는 것을 구하긴 했지만
점화식이 왜 이렇게 나오는지 잘 이해가 되지 않았다.
이어서 알아보도록 하자... 더보기

규칙이 뭘까...

우선 문제를 보면:
이친수는 0과 1로만 이루어진 수로, 다음의 조건을 따른다.
1. 이친수는 0으로 시작하지 않는다.
2. 이친수에서는 1이 두 번 연속으로 나타나지 않는다. 즉, 11을 부분 문자열로 갖지 않는다.

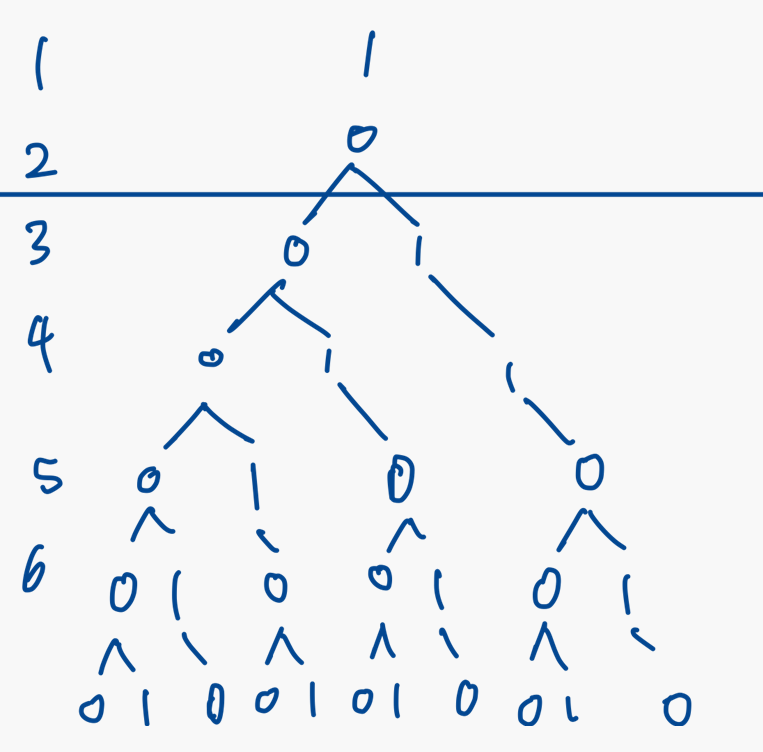
조건에 맞게 계속 쓰다 보면 n자리 이친수는 n-1자리 이친수들의 가장 끝에 0과 1을 붙인 것이라는걸 알 수 있다. 0으로 끝난다면 뒤에 0 또는 1을 붙일 수 있고, 1로 끝난다면 뒤에 0을 붙일 수 있다.
ex) 101 --> 1010 / 100 --> 1001, 1000

따라서 n자리 이친수의 개수는 n-1자리의 '0으로 끝나는 이친수'의 개수 *2 + '1로 끝나는 이친수'의 개수이다.

그럼 위의 식이 어떻게 dp[n]=dp[n-1]+dp[n-2]가 되는 것일까?

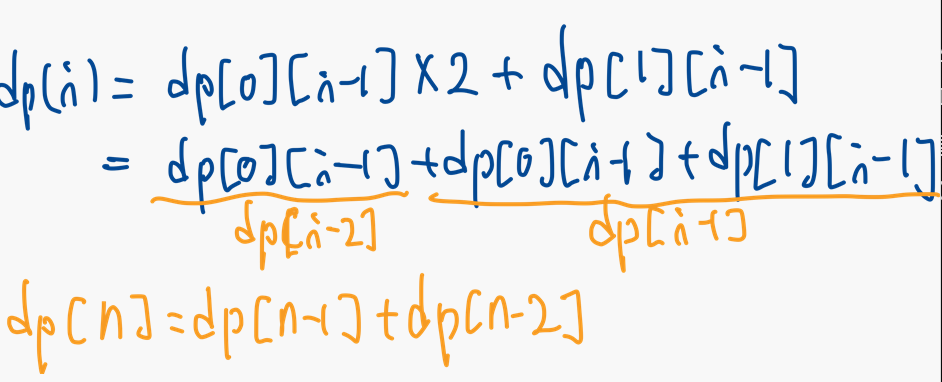
잘 정리하면 된다.

코드:

#include <iostream>
using namespace std;

long long int dp[100];

int main() {

	int n;
	cin >> n;
	dp[1] = 1;
	dp[2] = 1;
	for (int i = 3; i <= n; i++) {
		dp[i] = dp[i - 1] + dp[i - 2];
	}
	cout << dp[n];

	return 0;
}

점화식이 머리로는 이해됐지만 가슴으로는 이해되지 않아 계속 들여다봤던 문제다. dp 문제 중에선 쉬운 편이던데 아직은 부족한가 보다