
최소 비용 트리 (Least Spanning Tree)를 공부하다가 풀게 된 문제이다.
이 문제에서 크루스칼 알고리즘을 사용하여 풀었다.
최소 비용 트리는 보통 프림 알고리즘이나 크루스칼 알고리즘을 사용하여 푼다.
그 중 크루스칼 알고리즘에 대해 먼저 다뤄보겠다.
크루스칼 알고리즘이란?
크루스칼 알고리즘을 이해하기 위해서는 그리디 알고리즘과 Union Find에 대해 알고 있어야 한다.
그리디 알고리즘이란?
우선 그리디 알고리즘에 대해 간단하게 설명하자면 당장 눈 앞에 있는 것들 중 최선의 것을 선택하며 나아가는 알고리즘이다.
당장 눈 앞에 있는 경우의 수에서 최선을 선택한다. 따라서 미래의 경우에는 고려하지 않는 알고리즘이다.
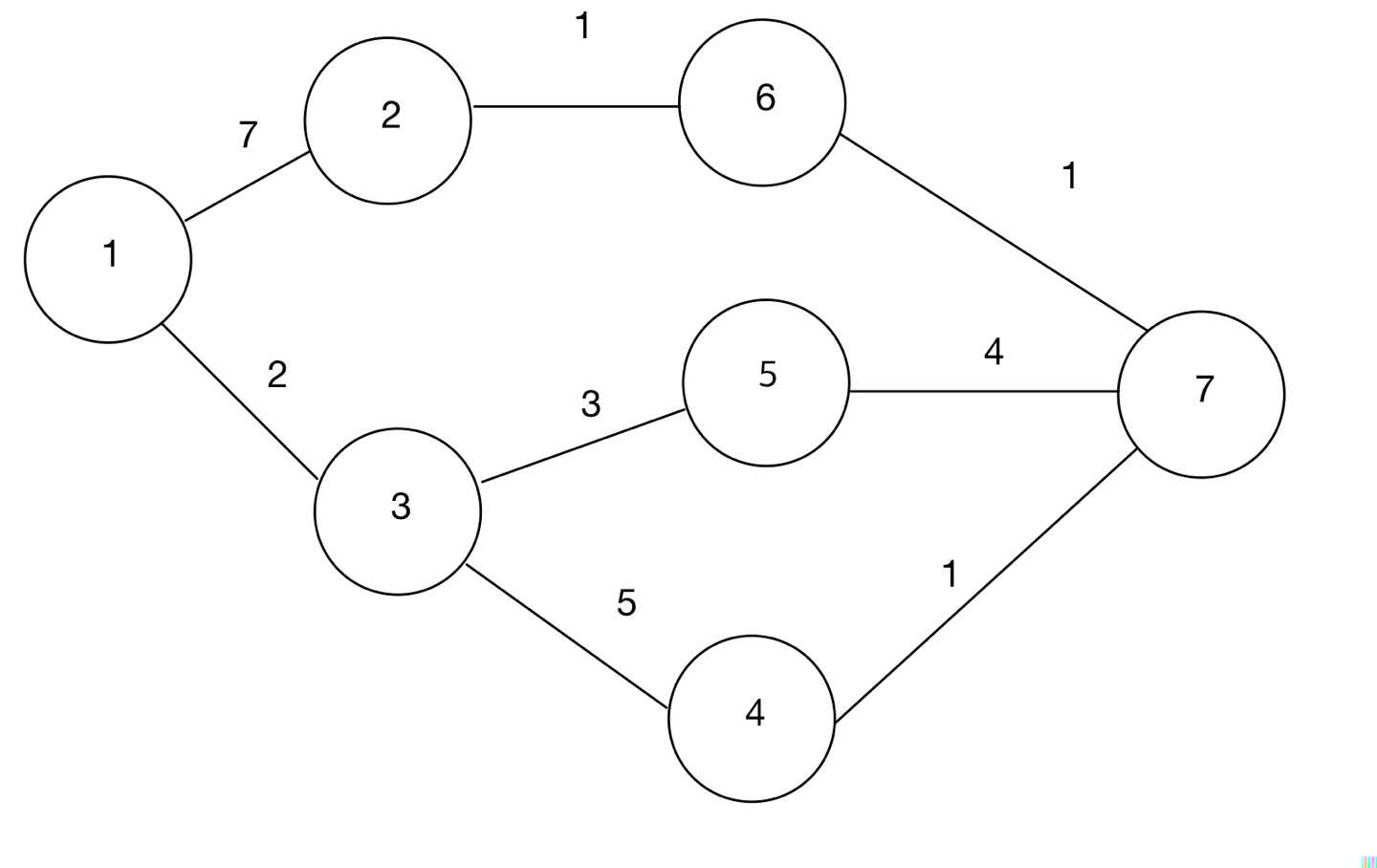
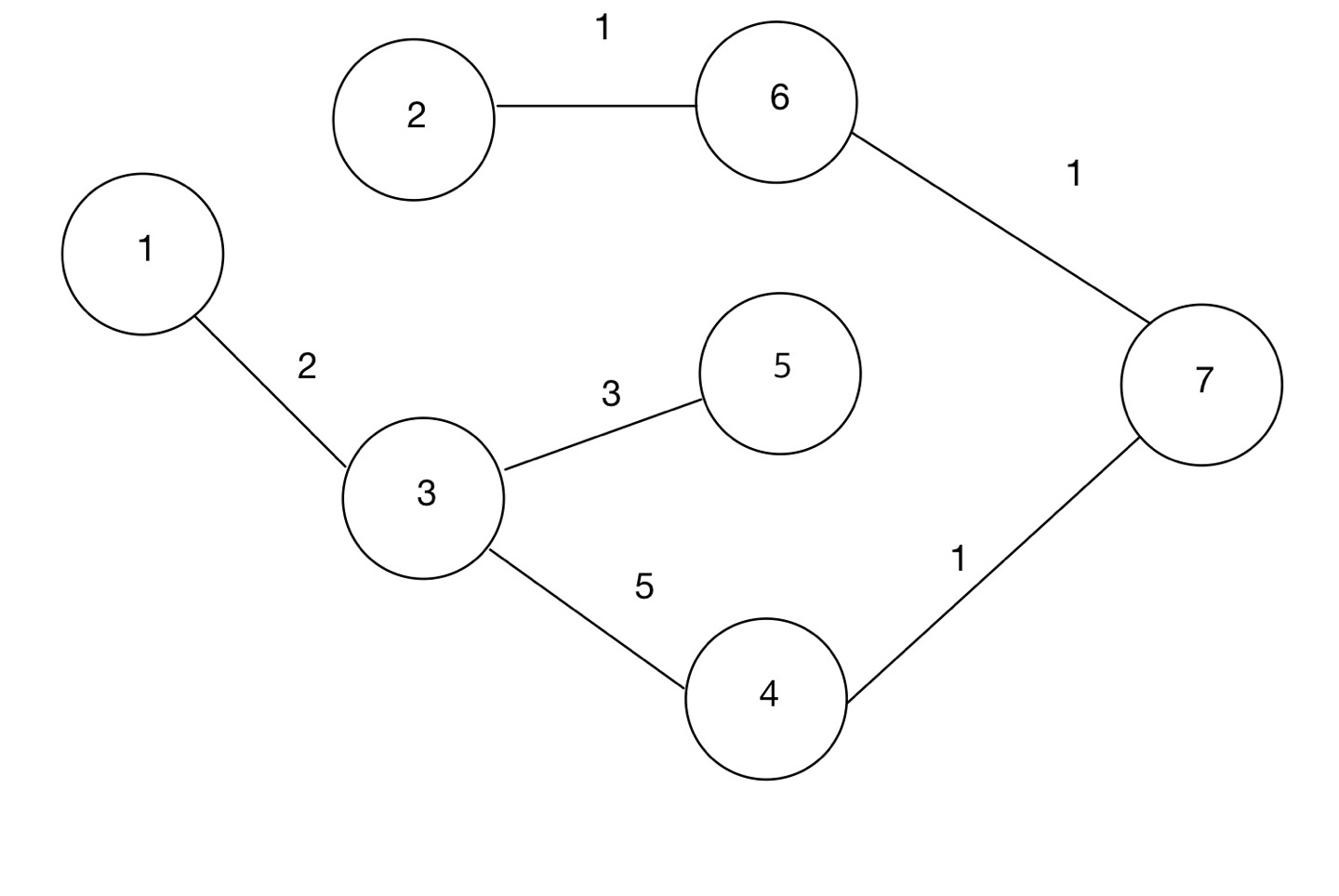
그림은 직접 그린 거라 조금 부족하다..
그림에서 1에서 7까지 가는 경로를 그리디 알고리즘으로 정한다면 1에서 가중치 7과 2 중 더 작은 2의 경로를 선택한다. 3에서는 가중치 3과 5 중 3을 선택하면 7까지 가는 총 가중치는 2 + 3 + 4 = 9가 된다.
그리디 알고리즘은 현재의 상황에서만 충실해야 하기 때문에 이와 같은 결과가 나오지만 보통 최선의 선택을 하려고 미래의 상황을 고려하면 1 - 3 - 4 - 7 의 경로를 선택하여 가중치가 2 + 5 + 1 = 8이 되어야 한다.
그러면 그리디 알고리즘이 어느정도 이해가 되었을 것이라고 생각한다.
그렇다면 이제 크루스칼 알고리즘에 대해 알아보자.
크루스칼 알고리즘
크루스칼 알고리즘은 그리디 알고리즘을 기반으로 한다.
기존의 그래프들의 간선에서 가중치가 감소하지 않는 순서로 에지 추가 여부를 결정하는데 에지가 사이클을 형성하지 않는다면 에지를 추가한다.
이렇게만 말하면 조금 헷갈릴 수도 있을것 같은데 그림을 통해 살펴보자.
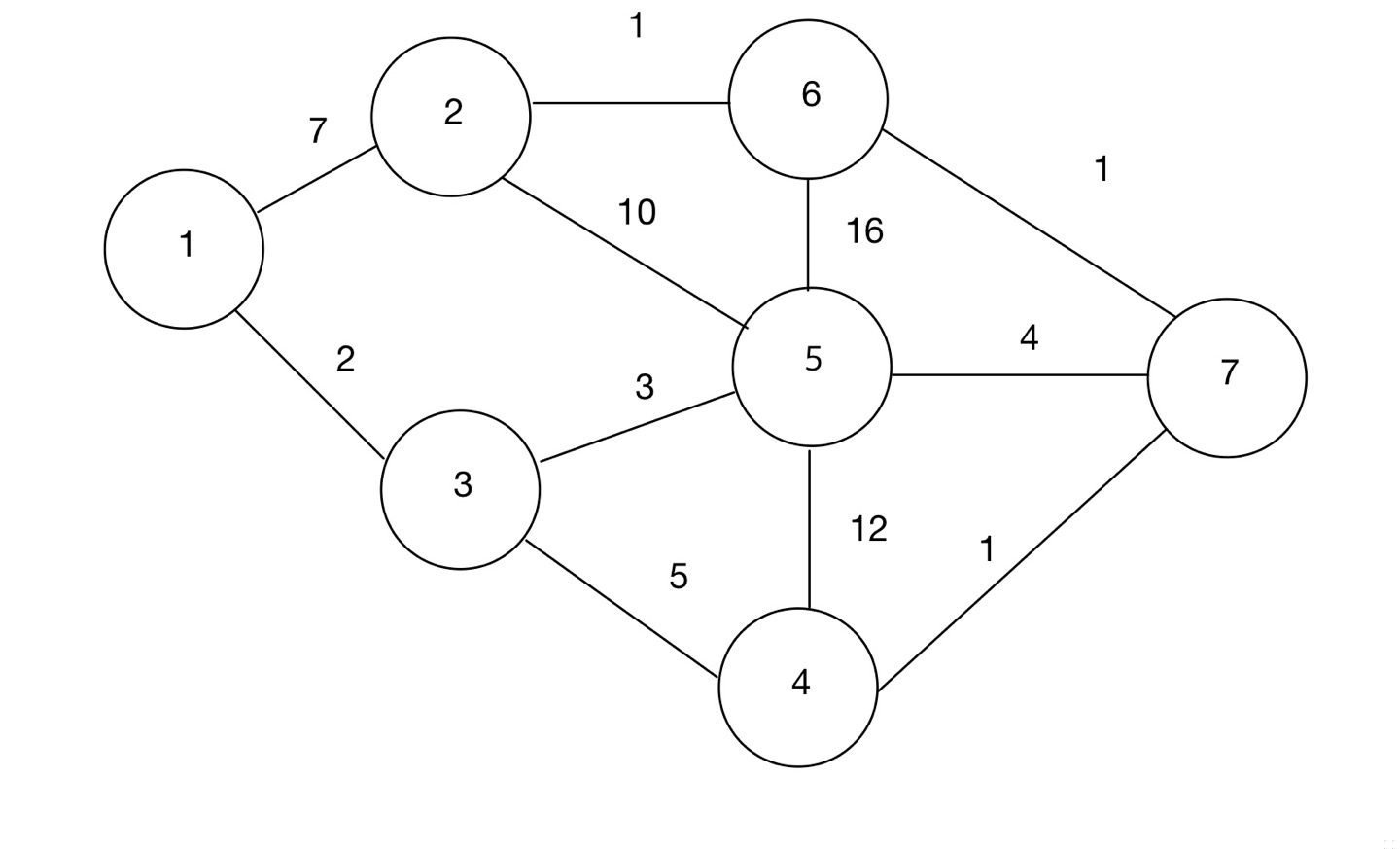
이러한 그래프가 존재한다고 가정하자. 그러면 우선 노드 들만 표시를 하면
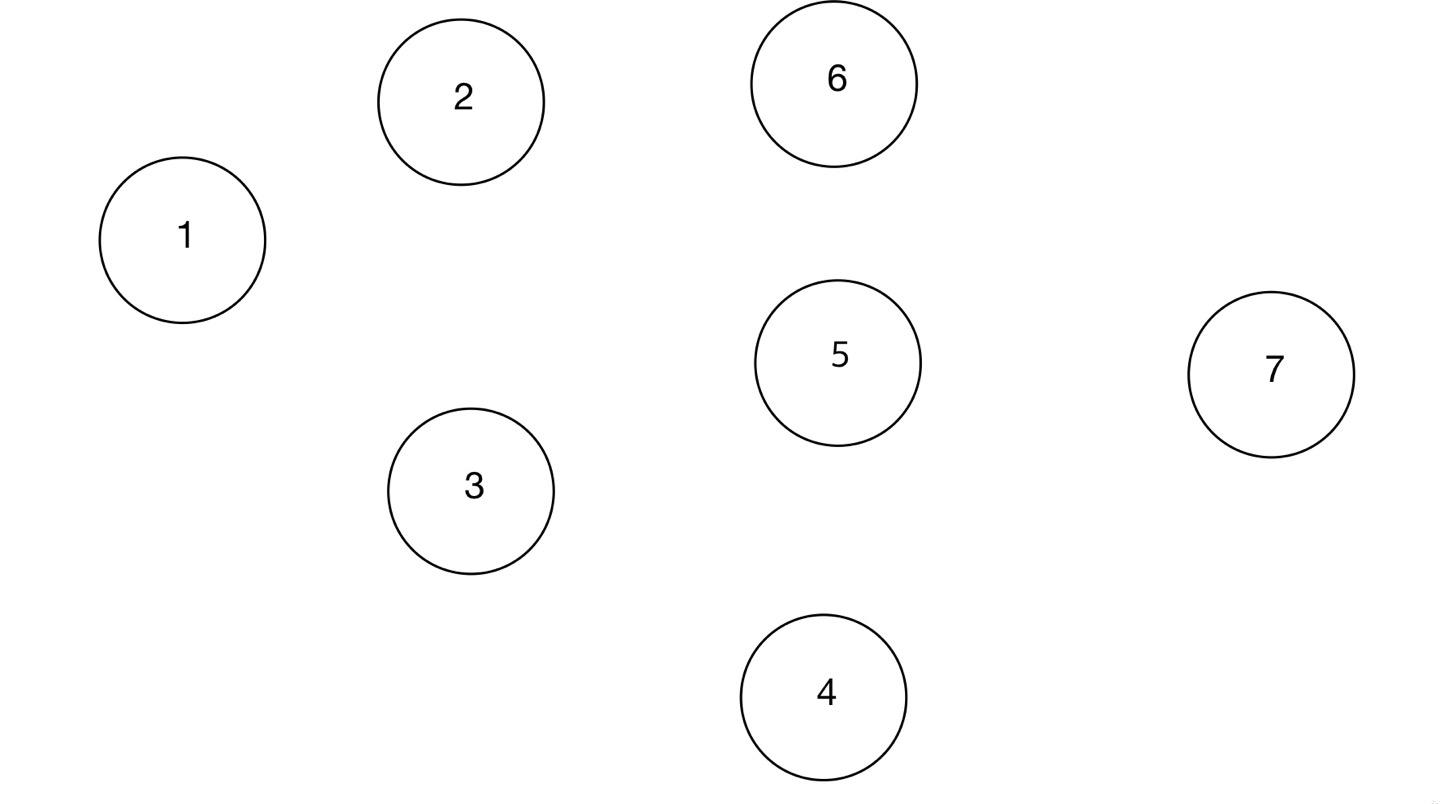
여기서 가중치가 작은 간선들부터 추가해나가는 것이다.
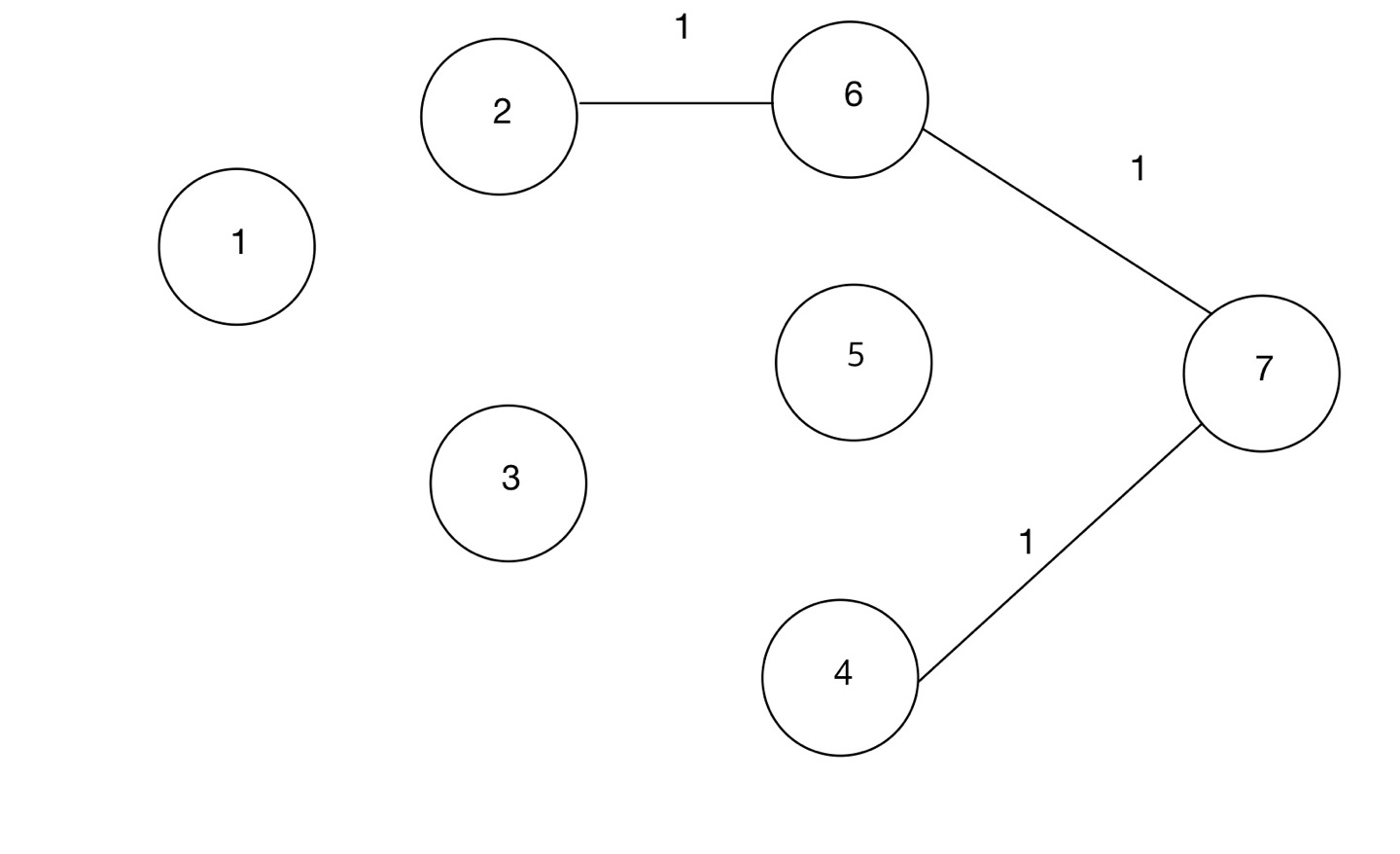
우선 가중치가 가장 작은 1 간선들 부터 추가한다.
이 간선들은 사이클을 형성하지 않기 때문에 추가될 수 있었다.
계속해서 사이클을 형성하지 않고 가중치가 작은 간선들부터 추가해나가면 위와 같은 최소 신장 트리가 완성된다.
크루스칼 알고리즘을 구현하면 가중치가 가장 작은 에지부터 차례로 고려할 수 있어야 하고, 추가한 간선이 사이클을 형성하는지 추가마다 확인해야한다.
이 과정에서 사이클 형성 여부를 Union-Find를 이용한다.
Union-Find란?
Union-Find는 Disjoint Set(분리 집합) 자료구조에서 사용하는 알고리즘이다.
Disjoint Set(분리 집합) 이란 서로 중복되지 않는 부분 집합들로 나눠진 원소들에 대한 자료구조이다.
Union-Find로 트리를 표현할 수 있다.
트리를 표현할 때 보통은 자신의 부모 노드를 연결해주어 트리를 구현하는 경우가 많은데 Union-Find는 자신의 부모 노드의 부모 노드를 계속해서 타고나가 루트 노드를 저장해준다.
한마디로 만약 두 노드가 같은 집합 즉, 같은 트리에 포함되어있다면 저장하고 있는 루트 노드가 같을 것이다.
그렇다면 어떻게 Union-Find로 사이클 생성 여부를 파악할까?
같은 트리에 포함되어있다면 루트 노드가 같은 것을 이용하여 파악하는 것이다.
그렇다면 이제 문제 풀이하면서 살펴도록 하고 넘어가자.
문제 풀이
문제에서 모든 컴퓨터가 연결되어 있어야 하는데 컴퓨터를 연결하는 비용을 최소화 해야 한다고 하였다.
그렇게 되기 위해서는 크루스칼 알고리즘이 바로 떠올랐다.
크루스칼 알고리즘을 통해 최소 스패닝 트리를 형성하면 그것의 가중치 합이 최소 비용이 될 것이다.
프림 알고리즘도 가능할 것이지만 크루스칼 풀이법으로 해결하였다.
크루스칼 알고리즘은 시간 복잡도가 Union-Find에 걸리는 시간 O(2m), 가중치를 미리 정렬하는데 힙을 사용하면 O(m), 에지를 제거할 때마다 O(log m) 시간이 걸리므로 크루스칼 알고리즘은 O(mlogm) 이라고 볼 수 있다.
하지만 필자는 정렬하는데 최소 힙을 사용하지 않고 그냥 sort()를 사용했음을 참고하길 바란다.
자세한 내용은 코드를 보면서 얘기하자.
import sys
read = sys.stdin.readline
n = int(read())
m = int(read())
lan = []
parent = [int(i) for i in range(n)]
for i in range(m):
a, b, c = map(int, read().split(' '))
lan.append([c, a - 1, b - 1])
def find(x):
if parent[x] != x:
return find(parent[x])
return x
def union(x, y):
fc = find(x)
sc = find(y)
if fc == sc:
return False
if fc > sc:
parent[fc] = sc
else:
parent[sc] = fc
return True
ans = 0
lan.sort()
for cost, com1, com2 in lan:
cycle = union(com1, com2)
if not cycle:
continue
ans += cost
print(ans)우선 Union-Find를 사용하기 위해 각각의 노드의 루트 노드를 저장하는 배열을 초기화해놓는다.
Lan선의 정보를 입력받으면 가중치를 우선으로 배열에 저장해준 후 오름차순으로 정렬해준다.
find()는 입력받은 노드의 루트 노드를 찾아주는 함수이다.
union()은 find()를 통해 루트 노드를 찾아주고 만약 루트 노드가 같다면 현재 두 노드는 같은 집합에 속해있다는 의미이므로 만약 간선이 추가되면 사이클이 형성된다.
따라서 루트가 같다면 False를 반환해주어 두 노드가 연결되지 않도록 하고 만약 루트가 다르다면 루트를 갱신해주어 간선을 추가해준다.
그리고 가중치를 더해주어 가중치의 총 합을 구한다.
그리고 이러한 가중치들은 아까 정렬한 Lan선의 오름차순 배열에서 차례대로 간선이 추가되고 계산되므로 가중치가 낮은 간선 부터 체크 + 사이클 생성 여부 체크 = 크루스칼 알고리즘을 완성했다고 볼 수 있다.
이렇게 크루스칼 알고리즘을 활용하여 문제를 풀어보았다.
프림 알고리즘 또한 최소 스패닝 트리 알고리즘이기 때문에 풀 수 있으니 궁금하다면 한 번 검색을 해보는 것도 좋을것 같다.
