20장. 코드 최적화 기법

Deah (김준희)·2024년 6월 18일

누구나 자료구조와 알고리즘 (개정2판)

목록 보기

17/17

지금까지 배운 내용을 통해 다양한 자료 구조에 대한 시간/공간 복잡도를 분석할 수 있다.
이러한 개념을 바탕으로 빠르고 메모리 효율적인 훌륭한 코드를 작성해보자.

20.1 전제 조건: 현재 빅 오 파악하기

알고리즘 최적화에 앞서 반드시 해야 할 전제 조건(prerequisite)은 현재 코드의 효율성을 파악하는 것이다. 현재 속도를 알아야 더 빠르게 만들 수 있기 때문이다. 다루는 알고리즘이 어떤 빅 오 카테고리에 속하는지 알아야 최적화를 할 수 있으므로 현재 알고리즘의 빅 오를 알아내는 단계를 전제 조건(prereq)이라고 부르겠다.

20.2 시작점: 상상할 수 있는 최상의 빅 오

이 기법은 모든 알고리즘에 유용하며 반드시 최적화 프로세스의 첫 단계여야 한다.

현재 알고리즘의 효율성을 알아냈으면 상상할 수 있는 최상의 빅 오를 생각해보자. (가능한 최상의 실행 시간)

상상할 수 있는 최상의 빅 오란 본질적으로 당면한 문제에 대해 기대할 수 있는 최상의 빅 오이며, 절대 달성할 수 없다고 믿는 빅 오이다. 예를 들어, 배열의 각 항목을 출력하는 함수를 작성할 때 상상할 수 있는 최상의 빅 오는 $O(N)$ 일 것이다. 배열 내 모든 항목에 접근하여 처리해야할 수밖에 없기 때문이다.

이렇게 알고리즘을 최적화 하기 위해서는 두 가지 빅 오를 밝혀내야 한다.

알고리즘의 현재 빅 오
작업에 걸릴 최상의 빅 오

두 개의 빅 오가 다르면 최적화 할 여지가 있다는 의미이다. 현재 알고리즘의 실행 시간이 $O(N^2)$ 이고 상상할 수 있는 최상의 빅 오가 $O(N)$ 이면 노력해볼 개선점이 생긴 것이다. 빅 오 간 차이는 최적화로 얻을 잠재적 이익을 나타낸다.

현재 알고리즘의 빅 오 카테고리 알아내기 (= 전제 조건)

문제를 해결할 수 있는 최상의 빅 오 알아내기

최상의 빅 오가 현재 빅 오보다 빠르면 최상의 빅 오에 가깝게 코드를 최적화 하기

물론 상상할 수 있는 최상의 빅 오를 항상 달성할 수는 없다. 현재 구현을 더 이상 최적화할 수 없을 수도 있다. 하지만 상상할 수 있는 최상의 빅 오는 최적화로 이뤄낼 수 있는 목표를 제시하는 도구이다. 보통은 현재 빅 오와 최상의 빅 오 사이쯤 속도로 알고리즘을 성공적으로 최적화한다.

상상의 나래 펼치기

앞서 살펴보았듯이 상상할 수 있는 최상의 빅 오는 최적화로 달성할 목표를 제시해주는 역할을 한다. 이러한 이점을 최대한 활용하기 위해서는 놀라운 상상력을 발휘해 최상의 빅 오를 생각해내는 것이 좋다.

또 하나의 사고 비결은, 당면한 문제를 해결할 정말 빠른 빅 오를 고르는 것이다. 이 방법을 '놀라운 빅 오(Amazing Big O)' 라고 부르겠다. 놀라운 빅 오를 골랐다면 "이것으로 문제를 해결할 수 있다고 믿을까?" 자문해보자. 놀라운 빅 오의 효율성으로 문제를 해결할 수 있다고 믿는다면 놀라운 빅 오를 상상할 수 있는 최상의 빅 오로 삼아보자.

여기까지 왔다면 알고리즘의 빅 오와 목표로 삼을 상상할 수 있는 최상의 빅 오가 준비된 것이다. 즉 최적화할 준비를 마쳤다. 이제부터는 코드의 효율성을 높이는 다른 최적화 기법과 사고 전략을 알아보자.

20.3 룩업 마법

최적화 기법 중 하나는 " $O(1)$ 시간 안에 마법처럼 원하는 정보를 찾을 수 있다면, 알고리즘을 더 빠르게 바꿀 수 있을까?" 하고 자문하는 방법이다. 대답이 "YES"라면, 주로 해시 테이블 같은 자료 구조를 사용해 마법을 부린다. 이 것을 룩업 마법이라고 부르겠다.

저자 룩업 마법

도서관에서 소프트웨어를 개발하며 책과 저자 데이터를 각각 두 개의 배열에 넣었다고 가정해보자.

authors 는 해시 테이블을 포함한느 배열이고, 각 해시 테이블은 저자의 이름과 ID를 포함한다. 그리고 books 도 다수의 해시 테이블을 포함하며, 책 데이터를 가지고 있다.

let authors = [
	{"author_id" => 1, "name" => "Virginia Woolf"},
	{"author_id" => 2, "name" => "Leo Tolstoy"},
	{"author_id" => 3, "name" => "Dr. Seuss"},
	{"author_id" => 4, "name" => "J. K. Rowling"},
	{"author_id" => 5, "name" => "Mark Twain"},
]

let books = [
	{"author_id" => 3, "title" => "Hop on Pop"},
	{"author_id" => 1, "title" => "Mrs. Dalloway"},
	{"author_id" => 4, "title" => "Harry Potter and the Sorcerer's Stone"},
	{"author_id" => 1, "title" => "To the Lighthouse"},
	{"author_id" => 2, "title" => "Anna Karenina"},
	{"author_id" => 5, "title" => "TheAdventures of Tom Sawyer"},
	{"author_id" => 3, "title" => "The Cat in the Hat"},
	{"author_id" => 2, "title" => "War and Peace"},
	{"author_id" => 3, "title" => "Green Eggs and Ham"},
	{"author_id" => 5, "title" => "The Adventures of Huckleberry Finn"}
]

books 에서 각 해시 테이블은 책 제목과 author_id를 포함하는데, 이것을 통해 authors 배열의 데이터에서 저자를 알아낼 수 있다.

예를 들어 "Hop on Pop"의 author_id는 3이다. authors 배열을 보면 Dr.Seuss의 ID가 3이므로 "Hop on Pop"의 저자가 Dr.Seuss라는 것을 알 수 있다.

이제 두 정보를 하나로 합쳐 아래와 같은 배열을 생성하는 코드를 작성해보자.

books_with_authors = [
	{"title" => "Hop on Pop", "author" => "Dr, Seuss"},
	{"title" => "Mrs, Dalloway", "author" => "Virginia Woolf"},
	{"title" => "Harry Potter and the Sorcerer's Stone", "author" => "J. K. Rowling"},
	{"title" => "To the Lighthouse", "author" => "Virginia Woolf"},
	{"title" => "Anna Karenina", "author" => "Leo Tolstoy"},
	{"title" => "The Adventures of Tom Sawyer", "author" => "Mark Twain"},
	{"title" => "The Cat in the Hat", "author" => "Dr. Seuss"},
	{"title" => "War and Peace", "author" => "Leo Tolstoy"},
	{"title" => "Green Eggs and Ham", "author" => "Dr. Seuss"},
	{"title" => "The Adventures of Huckleberry Finn", "author" => "Mark Twain"}
]

데이터를 위와 같이 구성하려면 books 배열을 순회하면서 각 책과 저자를 연결시켜줘야 한다.

첫 번째로는 중첩 루프를 사용하는 방법이 있다. 바깥 루프에서 각 책을 순회하고, 안쪽 루프에서 저자를 일일이 확인하며 각 책과 연결된 ID를 가지는 저자를 찾는 것이다.

function connectBooksWithAuthors(books, authors) {
  let booksWithAuthors = [];
  
  books.forEach(book => {
    authors.forEach(author => {
      if (book.author_id === author.author_id) {
        booksWithAuthors.push({
          title: book.title,
          author: author.name
        });
      }
    })
  })
  
  return booksWithAuthors;
}

이 알고리즘은 책 $N$ 개의 저자를 찾기 위해, 저자 $M$ 명의 루프를 순회해야 하므로 시간 복잡도가 $O(N * M)$ 이다.

최적화를 위해서는 상상할 수 있는 최상의 빅 오를 먼저 생각해보아야 한다. 예제에서는 책 $N$ 개를 무조건 순회해야 하므로 $O(N)$ 보다 더 빠를 수는 없어보인다. $O(N)$ 이 불가능은 아닌 생각할 수 있는 가장 빠른 속도이므로 상상할 수 있는 최상의 빅오로 삼아보자.

그 다음은 룩업 마법을 사용할 차례다. " $O(1)$ 시간 안에 마법처럼 원하는 정보를 찾을 수 있다면 알고리즘을 더 빠르게 바꿀 수 있을까?

이 질문을 예제에 적용해보자. 현재는 바깥 루프에서 모든 책을 순회한다. 안쪽 루프에서는 각 책에 대해 authors 배열에서 그 책의 author_id를 찾는다.

하지만 $O(1)$ 시간만에 저자를 찾는 방법이 있다면?
저자 한 명을 찾을 때 마다 모든 저자를 순회하지 않고 즉시 찾을 수 있다면?

이러한 경우 안쪽 루프를 사용하지 않을 수 있어 코드 속도를 $O(N)$ 으로 올릴 수 있으므로 알고리즘의 속도가 크게 향상된다.

자료 구조 추가하기

룩업을 실현할 가장 쉬운 방법 중 하나는 코드에 자료 구조를 추가하는 것이다. 이 자료 구조는 데이터를 빠르게 룩업할 수 있는 방식으로 데이터를 저장하는데 쓰인다. 대게 해시 테입르이 가장 적합한 자료 구조인데, $O(1)$ 만에 룩업이 가능하기 때문이다.

저자 정보가 현재는 배열에 저장되어 있어서, 주어진 author_id를 찾는데 항상 $O(M)$ 단계가 소요된다. (저자의 수) 하지만 같은 정보를 해시 테이블에 저장하면 각 저자를 $O(1)$ 시간만에 찾을 수 있다.

let authorHashTable = {
  1 => "Virginia Woolf", 
  2 => "Leo Tolstoy", 
  3 => "Dr. Seuss",
  4 => "J. K. Rowling", 
  5 => "Mark Twain"
}

function connectBooksWithAuthors(books, authors) {
  let booksWithAuthors = [];
  let authorHashTable = {};

  authors.forEach(author => {
    authorHashTable[author.author_id] = author.name;
  });

  books.forEach(book => {
    booksWithAuthors.push({
      title: book.title,
      author: authorHashTable[book.author_id]
    });
  });

  return booksWithAuthors;
}

먼저 authors 배열을 순회하며 해당 데이터로 authorHashTable을 생성한다. 이 때는 저자가 $M$ 명이면 $M$ 단계가 소요된다.

이어서 책 리스트를 순회하며 authorHashTable을 사용해 한 단계만에 저자를 찾는다. 이 때는 책이 $N$ 개이면 $N$ 단계가 소요된다.

최적화한 알고리즘은 책 $N$ 개를 순회하는 루프 하나와 저자 M명을 순회하는 루프 하나를 실행하므로 총 $O(N + M)$ 단계가 걸린다. 기존의 $O(N * M)$ 보다 훨씬 빠른 속도이다.

단, 추가 공간이 전혀 사용되지 않았던 기존 알고리즘과 다르게 해시 테이블을 추가로 생성하기 때문에 공간을 $O(M)$ 만큼 더 사용하게 된다. 속도를 위해 메모리를 기꺼이 희생할 수 있다면 대단한 최적화 효과이다.

두 수의 합(two-sum) 문제

마법 룩업으로 최적화 할 수 있는 또 다른 시나리오를 살펴보자.

두 수의 합 문제는 잘 알려진 코딩 문제이다. 숫자 배열을 입력받아 합해서 10(또는 주어진 다른 수)이 되는 두 수가 배열에 있는지를 true, false로 반환하는 함수를 작성하면 된다. (중복이 없다고 가정하겠다.)

let arr1 = [2, 0, 4, 1, 7, 9]

위와 같은 배열이 있다고 할 때, 1과 9를 합하면 10이 되므로 해당 함수는 true를 반환해야 한다.

let arr2 = [2, 0, 4, 5, 3, 9]

만약 배열이 위와 같다면 false를 반환해야 한다.

가장 먼저 떠오르는 방법은 중첩 루프를 사용해 매 수마다 다른 수들과 비교해 합해서 10이 되는지 알아보는 것이다.

function isTwoSum(array) {
	for (let i = 0; i < array.length; i++) {
    	for (let j = 0; j < array.length; j++) {
        	if (i !== j && array[i] + array[j] === 10) return true;
        }
    }
  
  	return false;
}

최적화를 시도하기 전에는 전제 조건을 이행하고 코드의 현재 빅 오를 알아내야 한다. 전형적인 중첩 루프 알고리즘처럼 isTwoSum 함수의 실행 시간은 $O(N^2)$ 이다.

다음으로 알고리즘이 최적화의 가치가 있는지 확인하려면 상상할 수 있는 최상의 빅 오를 생각해야 한다. 예제에서는 배열의 각 수를 무조건 1번 이상 방문해야 하므로 $O(N)$ 보다 좋을 수는 없다. 또 누군가 이 문제의 해법을 $O(N)$ 이라고 말해도 믿을 거 같다. 그러니 $O(N)$ 을 상상할 수 있는 최상의 빅 오로 삼자.

[2, 0, 4, 1, 7, 9] 배열 예제에서 바깥 루프를 머릿 속으로 한 단계씩 살펴보자. 이 루프는 첫 번째 숫자인 2부터 시작한다. 2를 순회할 때 어떤 정보를 룩업하고 싶은가? 2를 배열 내 다른 숫자와 더해서 10이 되는지를 알고 싶다. 한 발 더 나아가서 생각하면 2를 순회할 때 이 배열 어딘가에 8이 있는지를 알고싶은 것이다. 마법처럼 $O(1)$ 만에 룩업할 수 있고 배열에 8이 있는지 알게 되면 바로 true를 반환할 수 있다. 두 숫자를 합하면 10이 되므로 8을 2의 보수(counterpart)라고 부르자.

이제 데이터 구조를 추가해보자. 보통 가장 기본적인 옵션은 $O(1)$ 읽기가 가능한 해시 테이블이다. 배열 내 어떤 숫자든 $O(1)$ 안에 룩업해야 하므로 숫자를 해시 테이블에 키로 저장하자.

{ 2： true, 0： true, 4： true, 1： true, 7： true, 9： true }

이제 어떤 숫자든 $O(1)$ 안에 룩업할 수 있다. 그럼 보수는 어떻게 룩업할까?
기본적으로 어떤 숫자의 보수는 10에서 그 숫자를 빼서 계산한다.
$10 - 2 = 8$ 이므로 2의 보수는 8이다.

function isTwoSum(array) {
	let hash = {};
  
  	for (let i = 0; i < array.length; i++) {
    	if (hash[10 - array[i]) return true;
      	hash[array[i]] = true
    }
  
    return false;
}

이 알고리즘은 배열의 각 숫자를 한 번씩 순회한다. 각 수에 방문할 때마다 현재 숫자의 보수가 해시 테이블에 키로 있는지 확인한다. 어떤 숫자의 보수를 찾았으면 바로 true를 반환한다. 또한 각 숫자를 순회하며 그 숫자를 해시 테이블에 키로 삽입한다. 이런 식으로 배열을 검사해가며 각 숫자로 해시 테이블을 채운다.

이 방법에서는 알고리즘의 속도가 $O(N)$ 으로 급격히 빨라진다. 루프 내내 $O(1)$ 을 수행할 수 있도록 특별이 데이터 원소를 모두 해시 테이블에 저장함으로서 가능했다.

20.4 패턴 인식

코드 최적화와 알고리즘 개발에 전반적으로 쓰이는 가장 유용한 전략 중 하나가 패턴을 찾는 방법이다. 대게 문제에서 패턴을 발견하면 문제의 복잡도를 해소하고 실제로 간단한알고리즘을 개발할 수 있다.

동전 게임

동전 게임은 두 명의 플레이어가 다음과 같은 방식으로 경기를 치룬다. 동전 더미를 가운데 쌓아놓고, 각 플레이어가 동전 더미에서 차례대로 동전을 하나 혹은 두 개 없앤다. 마지막 동전을 없애는 플레이어가 게임에서 진다.

무작위 선택으로 승패가 갈리는 게임이 아니라 올바른 전략을 통해 상대방이 마지막에 동전을 가져가게 함으로써 게임에서 이길 수 있다.

동전 더미에 놓인 동전 개수가 주어졌을 때 게임에서 이길 수 있는지 계산하는 함수를 작성하려면 어떻게 해야 할까? 곰곰이 생각해보면 하위 문제를 사용함으로써 동전이 몇 개든 정확하게 계산알 수 있음을 깨닫게 된다. (하향식 재귀)

function gameWinner(numberOfCoins, currentPlayer = "you") {
  	if (numberOfCoins <= 0) {
      return currentPlayer;
  	}

  	let nextPlayer = currentPlayer === "you" ? "them" : "you";

  	if (gameWinner(numberOfCoins - 1, nextPlayer) === currentPlayer ||
      gameWinner(numberOfCoins - 2, nextPlayer) === currentPlayer) {
      return currentPlayer;
  	} else {
      return nextPlayer;
  	}
}

gameWinner 함수는 동전 개수와 어떤 플레이어가 게임할 차례인지를 받는다. 그리고 게임의 승자를 반환한다. 함수를 처음 호출할 때 cuurentPlayer는 "you"다.

기저 조건은 currentPlayer에 0개 이하의 동전이 남았을 때다. 즉, 상대방이 마지막 동전을 가져갔고, 현재 플레이어가 자동으로 게임에서 이기는 경우이다.

이어서 다음 플레이어를 저장할 nextPlayer 변수를 정의하고, 재귀를 수행한다.
현재 더미보다 동전이 한 개와 두 개씩 적은 동전 더미에 gameWinner 함수를 재귀적으로 호출해서 다음 플레이어가 이 시나리오에서 이기는지 지는지를 알아본다. nextPlayer가 두 시나리오에서 모두 지게되면 currentPlayer가 이긴다.

전제 조건 = 알고리즘의 현재 속도 = $O(2^N)$

상상할 수 있는 최상의 빅 오 = $O(1)$

예제 생성

문제마다 패턴이 고유하나 모든 문제에 걸쳐 유용한 패턴 찾기 기법을 하나 찾아냈다. 바로 수많은 예제를 생성하는 것이다. 많은 양의 예제 입력을 가져와 각각의 결과를 계산하고 패턴을 발견할 수 있는지 보자.

동전 더미의 크기가 1일 때부터 10까지 누가 승자인지 생각해보면 다음과 같다.

동전 개수	승자
1	상대방
2	당신
3	당신
4	상대방
5	당신
6	당신
7	상대방
8	당신
9	당신
10	상대방

명확한 패턴이 보인다. 기본적으로 코인 1개에서 시작해 2번에 걸러 1번씩 상대방이 이긴다. 나머지는 당신이 승자다. 즉, "them"은 동전 개수에서 1을 뺏을 때 3으로 나눠지는 수다. 이제 나눗셈 계산 하나로 누가 이길지를 알아낼 수 있다.

function gameWinner(numberOfCoins) {
  	if ((numberOfCoins - 1) % 3 === 0) {
    	return "them";
  	} else {
    	return "you";
  	}
}

numberOfCoins에서 1을 뺀 후 3으로 나눌 수 있다면 승자가 "them", 그렇지 않다면 승자는 "you"가 된다. 수학 연산 하나만 사용하는 알고리즘으로 시간과 공간 관점에서 모두 $O(1)$ 이다. 그리고 간단하다.

많은 예제를 입력해 패턴을 식별하고 문제를 해결할 수 있었다.

합 교환(sum swap) 문제

패턴 인식과 마법 룩업을 함께 사용해 알고리즘을 최적화 할 수 있는 예제를 살펴보자.

let array1 = [5, 3, 2, 9, 1]
let array2 = [1, 12, 5]

array1에 있는 숫자를 모두 합하면 20이고, array2에 있는 숫자를 모두 합하면 18이 된다. 함수는 서로 교환했을 때 두 배열의 합이 똑같아지는 숫자를 각 배열에서 하나씩 찾아야 한다. 위 예제에서는 1과 2가 된다.

let array1 = [5, 3, 1, 9, 1]   // 19
let array2 = [2, 12, 5]        // 19

이제 두 배열의 합이 똑같이 19가 됐다.

복잡해지지 않도록 함수에서 실제 교환을 수행하지 않고 교환해야 하는 두 수의 인덱스만 반환하겠다. (두 인덱스를 포함하는 배열로 반환) 방금 array1의 인덱스 2와 array2의 인덱스 0을 교환했으므로 [2, 0]을 반환하면 된다.

이 알고리즘을 작성하는 방법은 중첩 루프를 사용하는 것이다. 바깥 루프에서 array1의 각 숫자를 가리키고 안쪽 루프에서 array2의 각 숫자를 순회하며 두 숫자를 교환할 때 두 배열의 합을 확인한다.

전제 조건 = 알고리즘의 현재 속도 = $O(N * M)$

상상할 수 있는 최상의 빅 오 = $O(N + M)$

이제 문제에 숨겨진 패턴을 찾아야 한다.

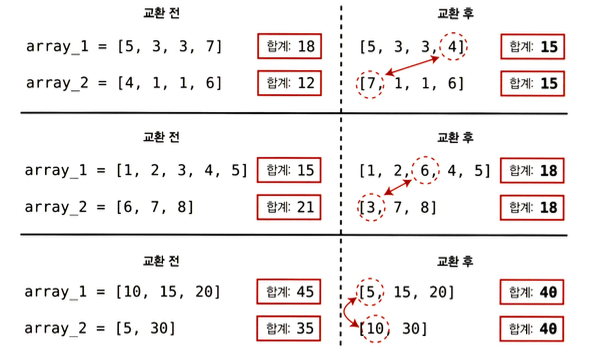
첫 번째 패턴은 합이 같아지려면 더 큰 배열에 있는 더 큰 수와 더 작은 배열에 있는 더 작은 수를 서로 교환한다는 것이다.

두 번째 패턴은 한 번 교환할 때 각 배열의 합이 같은 양만큼 바뀐다는 것이다. 예를 들어 7과 4를 교한하면 한 배열은 3만큼 작아지고, 나머지 배열의 합은 3만큼 커진다.

세 번째 패턴은 교환 후 각 배열의 합이 항상 두 배열 합 사이 중간에 떨어진다는 것이다.

이러한 패턴에 따라 각 배열의 합을 알면 배열 중 하나에 있는 어떤 숫자를 봤을 때 교환해야 하는 숫자를 계산할 수 있어야 한다.

let array1 = [5, 3, 3, 7]    // 18
let array2 = [4, 1, 1, 6]    // 12

18과 12의 가운데는 15다. 성공적인 교환을 위해서는 두 배열의 합이 15에 떨어져야 한다.

array1의 숫자들은 보며 어떤 숫자와 교환해야하는지 알아내보자. ("보수")
array1의 첫 번째 숫자인 5부터 시작하자.

5와 어떤 수를 교환해야 할까? array1이 3만큼 작아지고 array2가 3만큼 커지는 것을 알고 있으니 5와 2를 교한해야 한다. 불행하게도 array2에는 2가 없으므로 교환이 일어날 수 없다.

array1의 다음 숫자인 3을 보자. 두 배열의 합이 같기 위해서는 3을 array2의 0과 교환해야 하지만 array2에 0은 없다.

array1의 마지막 숫자는 7이다. 양 배열의 합이 15가 되려면 7과 4를 교환해야 한다. array2에 4가 있으므로 성공적으로 교환할 수 있다.

이 패턴을 어떻게 코드로 표현할까?
먼저 다음 계산으로 배열의 합이 얼만큼 변해야 하는지 알아낸다.

shift_amout = (sum1 = sum2) / 2

sum1은 array1의 합이고, sum2는 array2의 합이다. sum1이 18이고 sum2가 12이면 차이가 6이다. 이 차이를 2로 나누어 각 배열이 얼만큼 변해야 하는지 알아낸다.

예제에서 shift_amount는 3이므로 목표 합이 되려면 array2는 3만큼 커져야 한다.
따라서 두 배열의 합을 계산하는 알고리즘부터 만들어 나가야 한다. 다음으로 배열 하나의 숫자를 순회하며 나머지 배열에서 그 숫자의 보수를 찾는다.

예를 들어, array2에서 각 숫자를 순회한다면 앞서 보았듯 현재 숫자에 shift_amount를 더한 보수와 교환해야 한다. 현재 숫자가 4라면 그 보수를 찾기 위해 4에 shift_amount를 더해 7을 얻는다. 즉, 현재 숫자와 교환할 7을 array1에서 찾아야 한다.

이 패턴을 어떻게 활용해야 할까? 여전히 중첩 루프를 사용해야 하고, 알고리즘은 $O(N * M)$ 이다.

이 때 룩업을 활용할 수 있다. 어떤 숫자의 보수를 나머지 배열에서 O(1)만에 찾을 수 있으면 알고리즘이 훨씬 빨라질 수 있다. 먼저 한 배열의 숫자를 해시 테이블에 저장하면 나머지 배열을 순회하며 그 해시 테이블 내 어떤 숫자든 $O(1)$ 안에 바로 찾을 수 있다.

function sumSwap(array1, array2) {
  	let hashTable = {};
  	let sum1 = 0;
 	 let sum2 = 0;

 	 array1.forEach((num, index) => {
    	sum1 += num;
    	hashTable[num] = index;
  	});

  	array2.forEach(num => {
    	sum2 += num;
  	});

  	let shiftAmount = (sum1 - sum2) / 2;

  	for (let i = 0; i < array2.length; i++) {
    	let num = array2[i];
    	if (hashTable[num + shiftAmount] !== undefined) {
      		return [hashTable[num + shiftAmount], i];
    	}
  	}
  
  	return null;
}

이 방식은 기존 $O(N * M)$ 보다 훨씬 빠르다. array1의 크기가 $N$ 이고, array2의 크기가 $M$ 이면 최적화 이후 알고리즘은 $O(N + M)$ 시간에 실행된다.

이 방식은 array1의 숫자 $N$ 개를 전부 해시 테이블로 복사하므로 $O(N)$ 공간을 추가로 사용한다. 공간을 희생해 시간을 얻는 것이지만 속도가 중요하다면 큰 이득이 된다.

20.5 탐욕 알고리즘

탐욕은 가장 다루기 힘든 알고리즘의 속도를 올리는 전략이다. 모든 상황에 통하지는 않지만 일단 통하면 상황이 반전된다.

탐욕 알고리즘(greedy)은 매 단계마다 그 순간에 최선처럼 보이는 방법을 고르는 알고리즘이다.

배열 최댓값

배열에서 가장 큰 숫자를 찾는 알고리즘을 작성해보자.

중첩 루프로 각 숫자를 배열 내 나머지 숫자와 비교할 수 있다. 다른 모든 숫자보다 큰 숫자를 찾으면 배열에서 가장 큰 숫자를 찾은 것이다. 전형적인 중첩 루프 알고리즘처럼 이 방식은 $O(N^2)$ 시간이 소요된다.

배열을 오름차순으로 정렬해 배열의 마지막 값을 반환하는 방법도 있다. 퀵 정렬 같이 가장 빠른 정렬 알고리즘을 사용하면 $O(NlogN)$ 시간이 소요된다.

세 번째가 탐욕 알고리즘이다.

function max(array) {
  	let greatestNumber = array[0];
  
  	array.forEach(number => {
    	if (number > greatestNumber) greatestNumber = number;
  	})
  
  	return greatestNumber;
}

20.6 자료 구조 변경

( 추가 중 ... )

Deah (김준희)

기록 중독 개발자의 기록하는 습관

이전 포스트