8.1 서론

실험에서 관심있는 모수를 목표모수라고 합니다.
추정에는 점추정과 구간추정이 있고 간단하게 설명해보자면 아래와 같아요.

• 점추정: 모평균 $\mu$에 가까우리라 생각되는 하나의 수치를 사용
• 구간추정: 모평균 $\mu$가 두 수치 사이에 있을 것이라고 추정하여 모수가 포함되어있을 것 같은 구간을 만들어냄

정의 8.1
추정량은 표본에 포함된 측정값을 가지고 추정값을 어떻게 계산하는지를 알려주는, 일반적으로 공식으로 표현되는 규칙이다.

예를 들어, 표본평균

는 모평균 $\mu$의 하나의 점추정량이 되는거에요.
이해하기 더 쉬운 예제를 들어볼게요.
한 학급이 있습니다. 이 학급의 성적을 목표모수라고 하겠습니다.
학급의 성적을 보는 방법은 표본평균을 구해도 되고, 중앙값을 구해도 됩니다.
이렇게 다른 추정량을 사용하면 다른 추정값이 나오게 되는거죠.
이해 되시나요?
추정량은 표본평균, 중앙값, 표본분산같은 공식들이 되는거에요.
이를 통해 나온 값들이 추정량, 점추정량 같은 것들이 된답니다.
이러한 추정량들은 좋은 추정량, 나쁜 추정량이 있는데요.
누구는 평균이 더 좋아! 누구는 중앙값이 더 좋아! 할 수 있잖아요?
그럴 때 어떤게 더 좋은지, 잘 맞는지 판단을 하는 기준이 필요하겠죠?

---

8.2 점추정량의 편향(bias)과 평균제곱오차(MSE)

점추정은 표적에 사격하는 것과 비슷한데요. 추정값을 만들어내는 추정량은 권총, 추정값은 한 발에 비유할 수 있어요. 모수는 과녁의 정중앙이라고 생각을 하고 설명을 할게요.

모수의 추정값을 계산하는 것 = 한 발 쏘는 것

으로 볼 수 있겠죠?
만약 한 사람이 한 발을 쏴서 정중앙에 명중시켰다면, 뛰어난 사격이라고 하나요?
물론 뛰어나다고 할 수는 있지만 한 발에 대한 신뢰도는 높지 않을 거에요.
운으로 정중앙을 명중시킨건지 실력인지 아직은 모르죠.

반대로 100발을 쏴서 모두 정중앙 가까이에 명중시켰다고 해볼까요?
그럼 되게 정확도가 높다고 느껴지죠. 이때부터는 신뢰도가 높아지는 거에요.
여기서 알아야 할 점은 추정값을 한 번 구한다고 해서 절대로 점추정 절차의 우수성을 평가할 수 없다는 점이에요.

그렇게 추정절차를 매우 여러번 사용되었을 때 추정값들을 관찰해야 해요.
점추정에서의 추정값은 숫자니까 숫자들로 도수분표를 만들어 점추정량의 우수성을 평가하고,
이 도수분포가 얼마나 목표모수에 가까이 모여있는지 지켜봐야합니다.

편향

bias와 Unbias에 대해서 알아보려고 하는데요.
우선 모수 $\theta$의 점추정값을 구한다고 가정하죠.
$\theta$의 추정량을 $\hat\theta$(세타 햇)이라고 할게요.

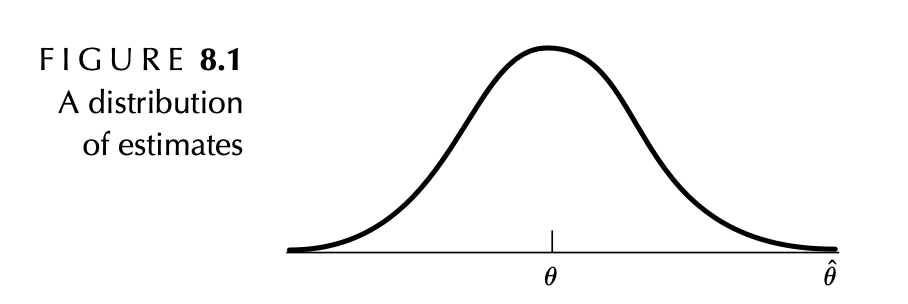
권총 예제를 생각하면 $\hat\theta$의 표집분포가 위의 그림 8.1과 같이 목표모수($\theta$)의 근처에 모여있는 것이 바람직해요.
즉, $E(\hat\theta)=\,\theta$. 이 성질을 만족하는 점추정량을 비편향(불편, unbias)이라 해요.

어디로 치우쳐지지 않았다라는 의미로 받아들여도 괜찮을 것 같아요.
그럼 편향은 무엇일까요?

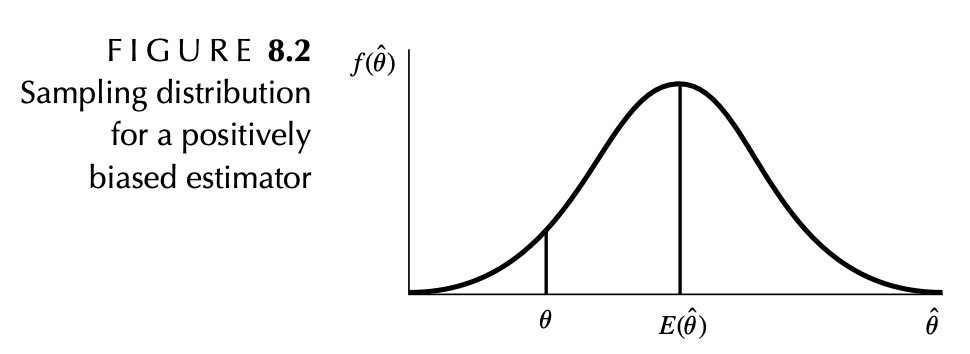
그림 8.2는 $E(\hat\theta)>\,\theta$인 양의 편향 점추정량의 표집분포에요.

정의 8.2
$\hat\theta$을 모수 $\theta$의 점추정량이라고 한다. 만약 $E(\hat\theta)=\theta$라면 $\hat\theta$은 비편향(불편) 추정량이다.
만약 $E(\hat\theta)\neq\theta$라면 편향 추정량이라고 한다.

정의 8.3
점추정량 $\hat\theta$의 편향 $B(\hat\theta)=E(\hat\theta)-\theta$로 주어진다.

여러분은 아래의 그림 중 어느 것을 선호하시나요?
사실 저는 아래 그림을 보고 둘 다 별로아닌가 생각을 했었는데요.

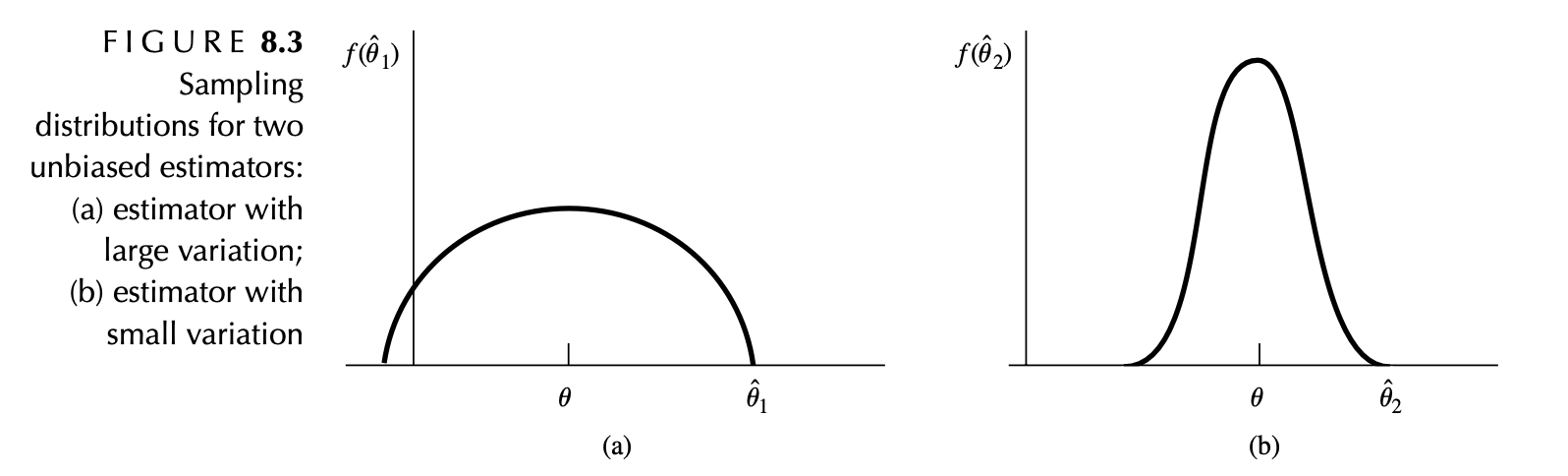
(a)는 큰 변동을 갖는 추정량
(b)는 작은 변동을 갖는 추정량입니다.
하지만 분산이 작을 수록 반복표집에서 $\hat\theta_2$이 $\theta$에 가까울 비율이 높아요.
이 말을 듣고 다시 그림을 보면 그래보이죠?

그러니까 이와 같이 비편향성에 더하여 $\hat\theta$의 분포의 분산 $V(\hat\theta)$이 가능한 작아지면 좋은 거죠.

점추정량의 우수성을 규정하기 위해서 편향($B(\hat\theta)$)과 분산($V(\hat\theta)$)를 사용하는 대신
추정량($\hat\theta$)과 목표모수($\theta$) 사이의 거리의 제곱의 평균

을 적용할 수 있다.

정의 8.4
점추정량 $\hat\theta$의 평균제곱오차(Mean Square Error)는

$MSE(\hat\theta) = E[(\hat\theta-\theta)^2]$

이다.

점추정량 $\hat\theta$의 평균제곱오차 $MSE(\hat\theta)$은 추정량의 분산과 편향의 함수로도 볼 수 있습니다.
만약 $B(\hat\theta)$가 추정량 $\hat\theta$의 편향을 나타낸다면

임을 보일 수 있어요.

증명은 다음에~

---

8.3 몇 가지 일반적인 비편향 점추정량

이번 절에서는 직관적으로 고려할 가치가 있는 점추정량을 볼거에요.
예를 들면, 모평균 $\mu$를 추정하기 위하여 표본평균 $\overline Y$을 사용하고,
이항모수 $p$를 추정하기 위하여 표본비율 $\hat p=\frac{Y}{n}$ 을 사용하는 것은 자연스럽죠.
그렇다면 서로 다른 두 모집단에서 $n_1$과 $n_2$개의 독립인 확률표본을 가지고 추론한다면 평균차$(\mu_1 - \mu_2)$ 혹은 두 이항모수의 차$(p_1-p_2)$는 어떻게 추정할까요?

생각보다 쉬운데요.
$(\mu_1 - \mu_2)$를 추정하기 위하여 표본평균의 차 $(\overline Y_1 - \overline Y_2)$를 사용하고,
$(\hat p_1-\hat p_2)$를 추정하기 위하여 표본비율의 차 $(\hat p_1-\hat p_2)$를 사용을 고려해야 합니다.
네 개의 추정량 $\overline Y,\, \hat p,\, (\overline Y_1 - \overline Y_2),\, (\hat p_1-\hat p_2)$은 확률변수의 함수이므로 기댓값과 분산을 구할 수 있어요.
확률표집인 경우, 네 추정량 모두 비편향이고 아래의 표에 나타난 표준편차를 갖는 것을 보일 수 있습니다.

가장 오른쪽에 있는 Standard Error는 말 그대로 표준오차를 말하는데요.
표준오차란, 추정량 $\hat\theta$의 표집분포의 표준편차, $\sigma_{\hat\theta}=\sqrt{\sigma_{\hat\theta}^2}$을 추정량 $\hat\theta$의 표준오차라 합니다.

-표본분산 불편추정량 증명-

---

8.4 점추정량의 우수성 평가

자 이제 우리가 진행한 점추정 절차의 우수성을 평가해보는 것을 배워야겠죠.
추정값과 목표모수와의 거리로 나타내는 방법이 있습니다.
반복표본에서 확률적으로 변하는 이 값을 추정오차(error of estimation)이라고 부릅니다.
당연히 추정오차가 적은걸 선호해요.

정의 8.5
추정오차 $\epsilon$은 추정량과 목표모수와의 거리이다. 즉, $\epsilon=|\hat\theta-\theta|$이다.

살짝 주의해야할 점은 "$\epsilon$이 0이면 비편향 추정량인가?"라는 궁금증이 생길 수도 있어요. 저는 그랬거든요.
근데 다시 한번 생각해보니 $B(\hat\theta)=E(\hat\theta)-\theta$이고 $E(\hat\theta) \neq \hat\theta$ 인 것 같더라구요. 그래서 둘이 다른거구나. 라고 생각하면 될 것 같습니다.