1.1 행렬 A의 열을 이용한 곱셈 Ax

1. 행렬 곱셈을 열의 조합으로 본 관점
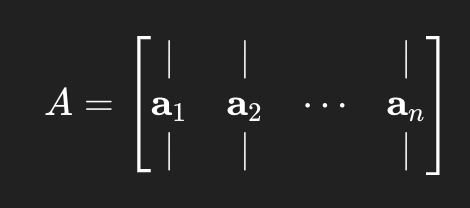
mxn 행렬 A = [a1, a2, ..., an]과 열벡터 $x=(x1, x2, ...xn)^T$가 있을 때, 곱 Ax는 다음과 같이 열 벡터들의 선형결합으로 해석할 수 있다.

$Ax = x_1a_1 + x_2a_2 + ... + x_na_n$

즉, Ax 결과는 열공간안에 존재하는 벡터이다.

• 열공간이란?
  행렬의 열벡터들로 생성되는 공간을 뜻한다, 즉 가능한 모든 선형 조합의 집합이다.

이 때 열 공간은 Col(A) = Span{$a_1, a_2, ..., a_n$} 이다. 열공간은 행렬 A의 열들이 존재하는 공간의 부분 공간이다.
A가 mxn 행렬이면, 열 벡터는 $R^m$에 속하므로 열공간은 $R^m$의 부분공간이 된다.
열공간의 차원은 그 행렬의 계수(Rank)와 같다. (즉, 선형독립인 열 벡터들의 개수)

• 열공간이 왜 중요한가?
  선형방정식 Ax=b의 해가 존재하는지 판단할 때 사용한다.
  벡터 b가 Col(A) 안에 있으면 해가 존재한다. b가 열공간 밖에 있으면 해가 없다.

2. 네 가지 핵심 개념
1. Column Space (열공간)
2. Row Space (행공간)
3. Rank (행렬의 계수: 독립 열벡터의 개수)
4. Gaussian Elimination (계수 및 기저 추출)

3. 열공간의 차원과 기저
열공간의 차원은 행렬의 랭크와 같고 이는 선형독립인 열의 개수이다.
Gaussian elimination을 통해 선형 독립인 열만 뽑아 basis로 삼으면 이 열들이 열공간을 완전히 생성한다.