플로이드 워셜 ( Floyd-Warshall )

플로이드-워셜 알고리즘은 모든 정점 쌍 사이의 최단 경로를 찾는 그래프 알고리즘이다.
이 알고리즘은 다익스트라와 달리 음의 가중치를 가지는 그래프에서도 사용할 수 있다.

플로이드 워셜의 핵심 은 A노드에 B노드까지 최단 경로를 구했다고 가정했을 때,
최단 경로 위에 K 노드가 존재한다면 그것을 이루는 부분 경로 역시 최단경로라는 것이다.

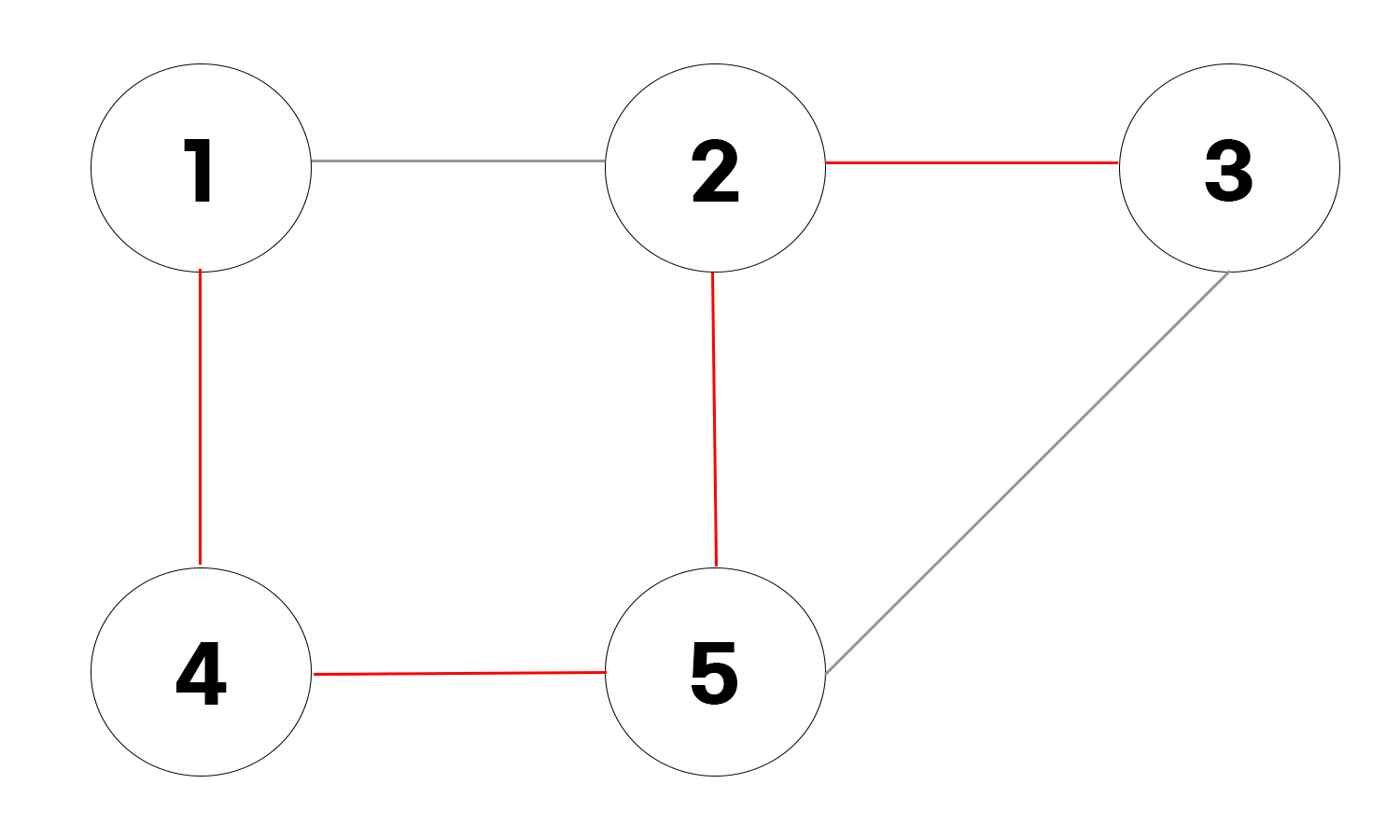
색칠된 에지 경로가 1 -> 3 이 최단 경로라면,
1 -> 5 경로와 5 -> 3 경로의 최단 경로 역시 색칠된 에지로 이뤄질 수 밖에 없다.

즉, 전체 경로의 최단 경로는 부분 경로의 최단 경로의 조합으로 이루어 진다는 뜻.

플로이드 워셜은 다이나믹 프로그래밍(DP)를 이용하여 구현된다.
구현 순서는 다음과 같다.

• 1. 인접행렬 배열을 선언하고 Start == End 를 0으로, 이외는 무한으로 초기화

        for (int i = 1; i <= N; i++) {
              for (int j = 1; j <= N; j++) {
                  if (i == j)
                      Dist[i][j] = 0;
                  else
                      Dist[i][j] = Integer.MAX_VALUE;
              }
         }

• 2. 최단 거리 배열에 그래프 데이터 저장
     Dist[Start][End] = Cost

      	  for (int i = 0; i < M; i++) {
                st = new StringTokenizer(br.readLine());
                int start = Integer.parseInt(st.nextToken());
                int end = Integer.parseInt(st.nextToken());
                int cost = Integer.parseInt(st.nextToken());
     
                // 값이 덧씌워질 경우 대비, 더 작은 값으로 업데이트
                if (Dist[start][end] > cost) {
                    Dist[start][end] = cost;
                }
            }

     
     

• 3. 점화식으로 배열 업데이트

           /*
           for ( 경유지 K에 관해 1 ~ N )
             for ( 출발노드 S에 관해 1 ~ N )
               for ( 도착노드 E에 관해 1 ~ N )
           */
     
           for (int k = 1; k <= N; k++) {
                for (int start = 1; start <= N; start++) {
                    for (int end = 1; end <= N; end++) {
                        Disth[start][end] = Math.min(Dist[start][end], Dist[start][k] + Dist[k][end]);
                    }
                }
            }

[ 백준 ] 플로이드

-  Java Code

    // N : 도시의 수(Node) , M : 버스의 수(Edge)
    static int N, M;

    // 가중치 그래프
    static int Graph[][];

    static final int Max_Value = 10000001;

    public static void main(String[] args) throws IOException {

        /*
         * 플로이드-워셜
         * 1. 인접행렬 배열을 선언하고 S==E를 0으로, 이외는 무한으로 초기화
         * 2. 최단 거리 배열에 그래프 데이터 저장 D[S][E] = W(가중치)
         * 3. 점화식으로 배열 업데이트
         *   for ( 경유지 K )
         *     for ( 출발노드 S )
         *       for ( 도착노드 E )
         * */

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;

        N = Integer.parseInt(br.readLine());
        M = Integer.parseInt(br.readLine());

        Graph = new int[N + 1][N + 1];

        // 1. 인접행렬 배열은 선언하고 S==E를 0으로, 이외는 무한으로 초기화
        for (int i = 1; i <= N; i++) {
            for (int j = 1; j <= N; j++) {
                if (i == j)
                    Graph[i][j] = 0;
                else
                    Graph[i][j] = Max_Value;
            }
        }

        // 2. 최단 거리 배열에 그래프 데이터 저장 D[S][E] = W(가중치)
        for (int i = 0; i < M; i++) {
            st = new StringTokenizer(br.readLine());
            int start = Integer.parseInt(st.nextToken());
            int end = Integer.parseInt(st.nextToken());
            int cost = Integer.parseInt(st.nextToken());

            // 값이 덧씌워질 경우 대비, 더 작은 값으로 업데이트
            if (Graph[start][end] > cost) {
                Graph[start][end] = cost;
            }
        }

        // 3. 점화식으로 배열 업데이트
        for (int k = 1; k <= N; k++) {
            for (int start = 1; start <= N; start++) {
                for (int end = 1; end <= N; end++) {
                    /*if (Graph[start][end] > Graph[start][k] + Graph[k][end]) {
                        Graph[start][end] = Graph[start][k] + Graph[k][end];
                    }*/
                    Graph[start][end] = Math.min(Graph[start][end], Graph[start][k] + Graph[k][end]);
                }
            }
        }

        for (int i = 1; i <= N; i++) {
            for (int j = 1; j <= N; j++) {
                if (Graph[i][j] == Max_Value) {
                    System.out.print("0 ");
                } else {
                    System.out.print(Graph[i][j] + " ");
                }
            }
            System.out.println();
        }

    }