Graph Search

2차원의 인접행렬로 구현된 그래프에서 정점을 탐색하는 알고리즘이다.
DFS, BFS 두 방법 모두 사용할 수 있지만 난 BFS의 방식이 더 이해가 잘됐다.

[ 백준 ] 유기농 배추
위 문제의 예시를 빗대어 사용하겠다.

2차원 행렬 Graph[][]에 다음과 같이 startNode, endNode 값을 저장하면

// Graph[i][j]
0 0
1 0
1 1
4 2
4 3
4 5
2 4
3 4
7 4
8 4
9 4
7 5
8 5
9 5
7 6
8 6
9 6

아래와 같은 행렬이 완성된다.

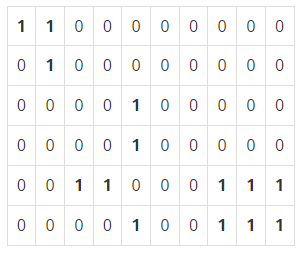
이같은 그래프 탐색 문제의 핵심은 현재 노드를 기준으로 상하좌우를 확인하는 것이다.

Graph[0][0] 부터 Graph[N][M] 까지 차례대로 탐색해가며
현재 노드의 상하좌우에 1이 존재한다면 Queue에 다음 노드의 좌표를 넣어
다시 그 노드의 상하좌우를 확인하는 방식으로 문제를 해결한다.

ArrayList와 달리 현재 좌표 x, y값을 Queue에 삽입해야하기 때문에

Queue<int[]> q = new LinkedList<>();

와 같은 형식으로 큐를 선언해야한다.

또한 상하좌우를 확인할 때 코드를 간결하고 이해하기 쉽게 쓸 수 있도록
상하좌우의 좌표를 계산할 1차원 배열 2개를 만든다.

int dx[] = { 0, 0, -1, 1 };
int dy[] = { -1, 1, 0, 0 };

// dx[i] 와 dy[i] 의 관계만 서로 중복되지 않도록 하면 되기 때문에 순서는 상관없다.

/* 
예를 들어 이런식으로도 사용할 수 있다는 것.
int dx[] = { -1, 1, 0, 0 };
int dy[] = { 0, 0, -1, 1 }; 
*/

이후 시작 좌표를 큐에 삽입하고 일반적인 BFS 탐색처럼 큐가 빌 때 까지 무한반복한다.

큐에서 좌표를 꺼내고 그 좌표의 상하좌우를 확인하는 방법은 다음과 같다.

		// 큐가 비어있으면 더이상 인접한 배추가 없다는 뜻
        while (!q.isEmpty()) {

            // 배추의 위치를 꺼냄
            int[] curr = q.poll();

            // 상하좌우 확인
            for (int i = 0; i < 4; i++) {
                int x = curr[0] + dx[i];
                int y = curr[1] + dy[i];

                // 좌표가 배추밭을 벗어나게되면 다음 좌표를 체크해야한다
                if (x < 0 || x >= M || y < 0 || y >= N) {
                    continue;
                }

                // 상하좌우 좌표에 배추가 있고, 방문하지 않았다면
                if (Graph[x][y] == 1 && Visited[x][y] == false) {
                    q.add(new int[]{x, y});
                    Visited[x][y] = true;
                }

            }

        }

이와 같은 형식으로 모든 좌표의 상하좌우를 확인하면서
이어져 있고 (Graph[x][y] == 1)
방문하지 않았다면 ( !Visited[x][y] == false)
큐에 삽입하는 방식으로 행렬의 끝까지 탐색하는 것이 그래프 탐색(BFS)의 기본이다.

-  Java Code


	static int Graph[][];
    static boolean Visited[][];
    static int M, N;

    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int T = Integer.parseInt(br.readLine());

        StringBuilder sb = new StringBuilder();
        StringTokenizer st;

        for (int testCase = 0; testCase < T; testCase++) {

            st = new StringTokenizer(br.readLine());

            // 가로
            M = Integer.parseInt(st.nextToken());

            // 세로
            N = Integer.parseInt(st.nextToken());

            // 배추의 개수
            int K = Integer.parseInt(st.nextToken());

            // 배추밭
            Graph = new int[M][N];

            // 배추밭 방문 여부
            Visited = new boolean[M][N];

            // 배추가 있어야할 위치에 배추 저장
            for (int i = 0; i < K; i++) {
                st = new StringTokenizer(br.readLine());
                int x = Integer.parseInt(st.nextToken());
                int y = Integer.parseInt(st.nextToken());

                // 배추 좌표 입력
                Graph[x][y] = 1;
            }
            // ==============================================
            // 입력된 내용 저장

            // 지렁이의 개수
            int earthWarm = 0;

            // 배추밭 탐색
            for (int i = 0; i < M; i++) {
                for (int j = 0; j < N; j++) {

                    // 배추가 존재하고 방문한적이 없는 지 확인
                    if (Graph[i][j] == 1 && Visited[i][j] == false) {
                        bfs(i, j);
                        earthWarm++;
                    }

                }
            }

            sb.append(earthWarm + "\n");

        }
        System.out.println(sb);

    }

    static void bfs(int startX, int startY) {

        // 방문한 위치를 true로 변경
        Visited[startX][startY] = true;

        // x, y 좌표를 저장할 Queue 배열 생성
        Queue<int[]> q = new LinkedList<>();

        // x, y 좌표를 q에 Push
        q.add(new int[]{startX, startY});

        // 상하좌우
        int dx[] = {0, 0, -1, 1};
        int dy[] = {-1, 1, 0, 0};
        // 배추가 상하좌우에 인접하면 이동할 수 있음
        // 현재 좌표에서 상하좌우 움직이는 좌표를 지정

        // 큐가 비어있으면 더이상 인접한 배추가 없다는 뜻
        while (!q.isEmpty()) {

            // 배추의 위치를 꺼냄
            int[] curr = q.poll();

            // 상하좌우 확인
            for (int i = 0; i < 4; i++) {
                int x = curr[0] + dx[i];
                int y = curr[1] + dy[i];

                // 좌표가 배추밭을 벗어나게되면 다음 좌표를 체크해야한다
                if (x < 0 || x >= M || y < 0 || y >= N) {
                    continue;
                }

                // 상하좌우 좌표에 배추가 있고, 방문하지 않았다면
                if (Graph[x][y] == 1 && Visited[x][y] == false) {
                    q.add(new int[]{x, y});
                    Visited[x][y] = true;
                }

            }

        }

    }