백준 1927번 최소 힙_ 을 풀며 공부하는 힙

드엔트론프·2023년 7월 23일

heap js 백준 1927 알고리즘 자료구조 자바스크립트 최소힙 힙

들어가며

힙에 대해 이전에 공부했었지만, 쓰지 않으면 까먹게 된다. 알고리즘을 풀며 때마침 힙이란 개념을 다시 공부하고 문제를 풀 기회가 생겨 풀며 기왕 공부한 거 정리까지 해보면 좋을 것 같아 정리해보려 한다.
이 문제는 제목처럼 최소 힙을 구현하여 풀면 된다.

기본적으로 트리의 구조. 특별히 추가되는 규칙이 있음

이진 힙 Binary Heap

이진 탐색 트리와 매우 유사한데, 몇몇 규칙이 다르다.
이진 탐색 트리처럼 최대 2개의 노드를 갖는다.
왼쪽, 오른쪽 크고 작고의 기준은 없다.
형제 노드 사이에는 그런 내용이 보장되지 않는다.
언제나 최적의 용량을 가진다. 각 노드의 모든 하위 항목이 최대한 가득 차 있고 왼쪽 하위 항목이 먼저 채워진다.

최대 이진 힙 MaxBinaryHeap → 부모 노드는 항상 자식 노드보다 크다.

최소 이진 힙 MinBinaryHeap → 부모 노드는 항상 자식 노드보다 작다.

Big-O (최고, 최악 모두)

삽입 - log(n)

삭제 - log(n)

탐색 - O(n)

문제

널리 잘 알려진 자료구조 중 최소 힙이 있다. 최소 힙을 이용하여 다음과 같은 연산을 지원하는 프로그램을 작성하시오.

배열에 자연수 x를 넣는다.
배열에서 가장 작은 값을 출력하고, 그 값을 배열에서 제거한다.
프로그램은 처음에 비어있는 배열에서 시작하게 된다.

입력

첫째 줄에 연산의 개수 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 N개의 줄에는 연산에 대한 정보를 나타내는 정수 x가 주어진다. 만약 x가 자연수라면 배열에 x라는 값을 넣는(추가하는) 연산이고, x가 0이라면 배열에서 가장 작은 값을 출력하고 그 값을 배열에서 제거하는 경우이다. x는 231보다 작은 자연수 또는 0이고, 음의 정수는 입력으로 주어지지 않는다.

출력

입력에서 0이 주어진 횟수만큼 답을 출력한다. 만약 배열이 비어 있는 경우인데 가장 작은 값을 출력하라고 한 경우에는 0을 출력하면 된다.

예제 입력 1

예제 출력 1

최소 이진 힙 insert 구현하기

최소 이진 힙을 구현하려면 어떤게 필요할까? 간단히 생각해보자면, 트리 구조의 형태에서 부모가 되는 가장 첫번째 요소가 가장 작은 수이고, 가장 작은 수가 제거될 때마다(부모가 빠질 때마다) 자식들 중 가장 작은 값이 부모의 자리로 가면 된다.
그러면 어떤 기능들이 있어야할까? 먼저, 값을 넣어야 힙을 구현하든말든 하니 값을 넣는 코드를 만들면 될 것 같다. 하지만 값을 push하듯 순서대로 넣으면 그건 그냥 배열이지 힙이 아니다. 어떻게 넣을까?
일단 값을 넣고, 들어간 값이 내 부모보다 큰 지 작은지를 판단한다. 그리고 부모보다 작다면 부모와 자리를 바꾸면 된다. 이 방식을 계속해서 반복하게되면 숫자들은 각 자리에 맞게 갈 것이다.
이 내용을 다시 의사코드로 정리해보자면 아래와 같다.

값을 입력하는 insert 메소드를 작성한다.

알맞은 자리로 갈 때까지 ‘버블업’한다.

프로퍼티 - 1의 값을 갖는 index 라는 변수를 만든다.

(index-1) /2 를 내림한 parentIndex 변수를 만든다.

parentIndex(부모 인덱스 자리에 있는 값)가 자식 인덱스보다 크다면,

둘을 스왑한다.

스왑 후 인덱스를 부모 인덱스로 다시 설정해준다.

코드로 보자면 다음과 같다.

  insert(element) {
    this.values.push(element);
    this.bubbleUp();
  }

  bubbleUp() {
    let idx = this.values.length - 1;
    const element = this.values[idx];
    while (idx > 0) {
      let parentIdx = Math.floor((idx - 1) / 2);
      let parent = this.values[parentIdx];
      if (element >= parent) break;
      this.values[parentIdx] = element;
      this.values[idx] = parent;
      idx = parentIdx;
    }
  }

참고로 this.values는 빈 배열로 시작한다.

이진 트리의 구조상 부모의 인덱스는 (index-1) /2 를 내림한 값(Math.floor)으로 알 수 있다.
예를 들어 배열에 [ 1, 2, 3, 4, 5, 6] 이 있다면

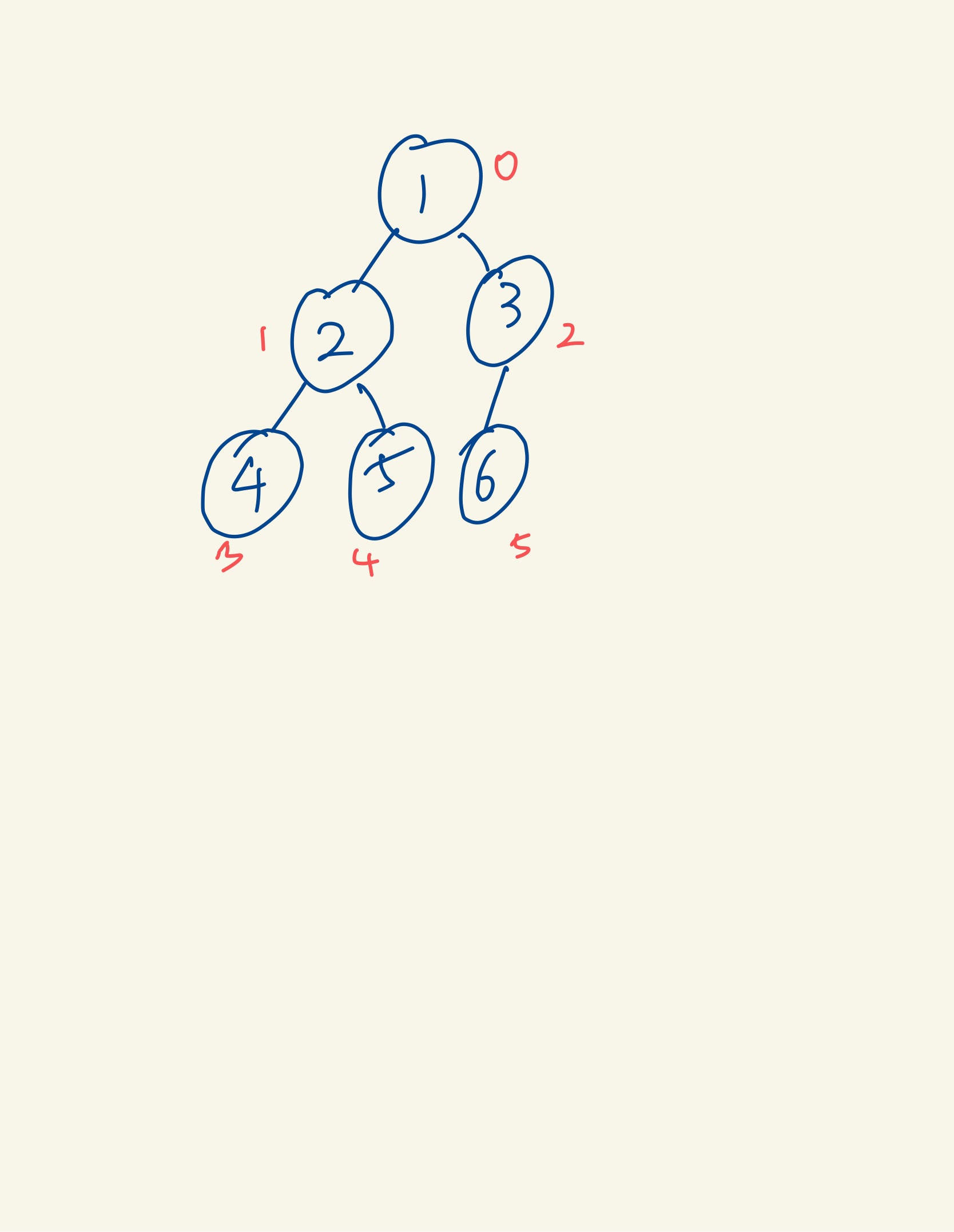
이런 형태일 것이다. 여기서 6의 부모는 3으로, 6의 인덱스인 5 - 1 /2 를 하면 3의 인덱스인 2가 나온다.

최소 이진 힙 remove 구현하기

값을 넣을 수 있다면 뺄 수도 있으면 좋을 것 같다. 대부분 힙을 구현하는 이유는 최소 이진 힙일때는 최소값을 출력하고, 최대일때는 최대값을 출력하는 게 주요한 이유라고 생각한다. 이 출력을 위해서는 삽입과 삭제가 필요한데, 힙의 구조가 삽입과 삭제 속도가 매우 빠르기 때문이다.
그렇다면 remove는 어떻게 구할 수 있을까? 일단 최소값은 당연하게도 부모 노드이다. 부모를 출력하고, 그다음엔? 어느 자식이 가장 작은지를 하나하나 일일이 찾아봐야할까? 그러면 힙을 사용할 이유가 없는 것 같다. 힙은 이러한 remove를 내가 생각하지 못하는 멋진 방식으로 구현한다. 아래의 의사코드를 보자.

제일 앞에 있는 값을 가장 뒤에 있는 값과 바꾼다.

제일 뒤로 간 값을 제거한다. (pop)

새로운 루트를 ‘sink down’ 하여 알맞은 위치로 간다.

기본적으로 루트 자리인 인덱스 0에서 시작한다.

왼쪽 자식의 인덱스를 찾는다 → 2* 인덱스 + 1 (범위를 벗어나지 않도록 해줘야한다)

오른쪽 자식의 인덱스를 찾는다 → 2* 인덱스 + 2 (범위를 벗어나지 않도록 해줘야한다)

왼쪽 혹은 오른쪽의 자식이 작다면 스왑한다. 둘 다 작다면 둘 중 더 작은 자식과 스왑한다.

바꾼 자식 인덱스는 새로운 부모 인덱스가 된다.

어느 자식도 해당 요소보다 작지 않을때까지 스왑해준다.

pop 한 맨 처음 루트를 반환한다.

최소값은 배열의 0번째 인덱스다.
의사코드에 맞게 배열의 맨 끝 값을 pop한다.
sinkDown을 하기 전에 배열에 값이 들어있어야하니, values의 길이가 0을 초과할 때 아까 pop 한 맨 끝값을 부모인 0번째 인덱스로 넣어두고, 본래의 위치에 갈 수 있도록 sinkDown 해준다.
당연하게도 최소값을 반환한다.

  extractMin() {
    const min = this.values[0];
    const end = this.values.pop();

    if (this.values.length > 0) {
      this.values[0] = end;
      this.sinkDown();
    }
    return min;
  }

그렇다면 이제 의사코드로 작성했던 sinkDown이 어떻게 코드로 구현할 수 있는지 살펴보자.

sinkDown() {
    let idx = 0;
    const length = this.values.length;
    const element = this.values[0];

    while (true) {
      let leftChildIdx = 2 * idx + 1;
      let rightChildIdx = 2 * idx + 2;
      let leftChild, rightChild;
      let swap = null;

      if (leftChildIdx < length) {
        leftChild = this.values[leftChildIdx];
        if (leftChild < element) {
          swap = leftChildIdx;
        }
      }

      if (rightChildIdx < length) {
        rightChild = this.values[rightChildIdx];
        if (
          (swap === null && rightChild < element) ||
          (swap !== null && rightChild < leftChild)
        ) {
          swap = rightChildIdx;
        }
      }
      if (swap === null) break;
      this.values[idx] = this.values[swap];
      this.values[swap] = element;
      idx = swap;
    }
  }

sinkDown에서도 중요한 부분은 왼쪽과 오른쪽 자식 인덱스를 구하는 부분으로 보인다.
let leftChildIdx = 2 * idx + 1;
let rightChildIdx = 2 * idx + 2;

이제 힙을 구현했으니 문제인 최소 힙에 적용해보자.

const path = process.platform === "linux" ? "/dev/stdin" : "input.txt";
const fs = require("fs");
const [N, ...arr] = fs
  .readFileSync(path)
  .toString()
  .trim()
  .split(`\n`)
  .map(Number);

class MinBinaryHeap {
  constructor() {
    this.values = [];
  }
  insert(element) {
    this.values.push(element);
    this.bubbleUp();
  }

  bubbleUp() {
    let idx = this.values.length - 1;
    const element = this.values[idx];
    while (idx > 0) {
      let parentIdx = Math.floor((idx - 1) / 2);
      let parent = this.values[parentIdx];
      if (element >= parent) break;
      this.values[parentIdx] = element;
      this.values[idx] = parent;
      idx = parentIdx;
    }
  }

  extractMin() {
    const min = this.values[0];
    const end = this.values.pop();

    if (this.values.length > 0) {
      this.values[0] = end;
      this.sinkDown();
    }
    return min;
  }

  sinkDown() {
    let idx = 0;
    const length = this.values.length;
    const element = this.values[0];

    while (true) {
      let leftChildIdx = 2 * idx + 1;
      let rightChildIdx = 2 * idx + 2;
      let leftChild, rightChild;
      let swap = null;

      if (leftChildIdx < length) {
        leftChild = this.values[leftChildIdx];
        if (leftChild < element) {
          swap = leftChildIdx;
        }
      }

      if (rightChildIdx < length) {
        rightChild = this.values[rightChildIdx];
        if (
          (swap === null && rightChild < element) ||
          (swap !== null && rightChild < leftChild)
        ) {
          swap = rightChildIdx;
        }
      }
      if (swap === null) break;
      this.values[idx] = this.values[swap];
      this.values[swap] = element;
      idx = swap;
    }
  }
}


let heap = new MinBinaryHeap();
let result = "";

for (let i = 0; i < N; i++) {
  if (arr[i] === 0) {
    result += (heap.extractMin() || 0) + "\n";
  } else {
    heap.insert(arr[i]);
  }
}
console.log(result.trim());

마치며

처음에 class로 heap을 구현 후 출력 부분에서 바로 console을 찍으려고 했더니 이것도 시간초과가 나더라. 시간초과 너무 싫어

//시간초과
for (let i = 0; i < N; i++) {
  if (arr[i] === 0) {
    if (heap.values.length > 0) {
      console.log(heap.extractMin());
    } else console.log(0);
  } else {
    heap.insert(arr[i]);
  }
}