Partial Regression
Linear Regression model에서 예측변수가 여러개일 때, 즉 multiple linear regression인 경우 각각의 변수 고유의 영향력을 파악하는 방법으로 partial regression이 있다(Partial Least Square algorithm과 명백히 다르다!). 이에 대해 간단히 다루어보도록 하자. 우선 다음과 같은 회귀모형
이 존재한다고 하자. 이때, 예측변수 중 만을 사용하여 다음과 같이 새로운 모형을 만든다고 하자.
그러면, 행렬 가 직교하지 않는 한 OLSOrdinary Least Square를 이용해 추정한 회귀계수에 대해서 이 성립한다(아래 참고).
Full Model에 대한 Least squares:
Reduced Model에 대한 Least squares:
로 주어지므로, 식 (1)에서 인 조건이 주어지면 이 성립한다.
하지만 일반적으로 두 예측변수 행렬이 직교하는 경우는 거의 존재하지 않으므로, 예측변수 에 대해 Full-Model에서의 회귀계수(벡터)와 Reduced-Model에서의 회귀계수는 편차가 존재하게 된다. 이와 관련하여 다음 정리가 성립한다.
Frisch-Waugh-Lovell프리슈-워-로벨 THM
FWL Theorem이라고도 하는 위 정리는 앞서 설명한 Full Model과 Reduced Model 간의 관계와 관련한 정리이다. 앞선 상황처럼 가 예측변수로 주어진다고 하자. 이제 다음 두 단계를 진행하자.
- 반응변수 를 로만 Regression하여(Reduced Model) 이때의 잔차를 라고 두자.
- 나머지 예측변수 를 로 Regression하여 이때의 잔차를 라고 하자.
이때 을 반응변수로, 를 예측변수로 하는 선형회귀모형의 회귀계수와 Full Model에서의 는 동일하다.
증명.
먼저 1단계에서의 잔차를 구하면 다음과 같다.
여기서 는 identity matrix, 는 Hat Matrix이다. 마찬가지로, 이번에는 2단계에서의 잔차를 구해보도록 하자.
이를 바탕으로 와 를 이용한 회귀계수 를 구하면
이때 은 idempotent, symmetric 하므로
으로 주어진다. 반면, Full Model에서 의 계수를 구하면 위 식 (1)의 Block Matrix의 역행렬을 구하는 것으로부터 가 와 동일하게 주어짐을 확인할 수 있다. (Block Matrix의 역행렬을 구하는 것은 어렵진 않으나 작성의 어려움으로 인해 생략)
Partial Regression Plot
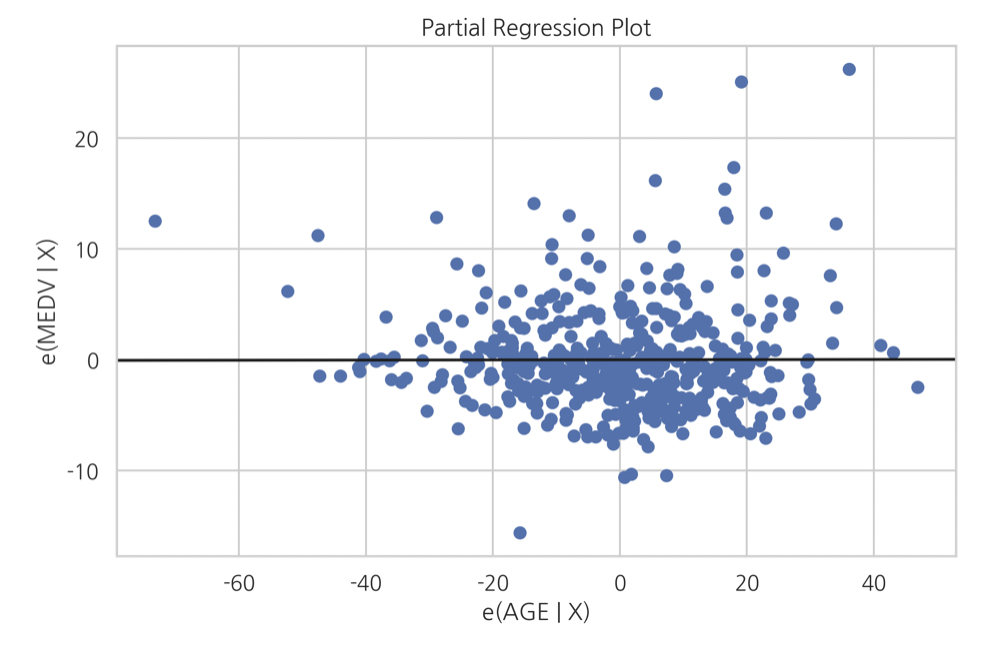
데이터 분석에서는 선형모형의 변수 유의성을 확인하기 위해 Partial Regression Plot을 확인하는 경우가 종종 있다. 앞선 FWL 정리의 두 잔차 의 scatter plot과 Regression plot(Line)을 함께 나타낸 것이 Partial Regression Plot으로, 두 잔차는 모두 해당 변수()로부터 다른 변수들(각각 , 전체)의 영향을 제거했다는 점에서 의미가 있는 벡터이다.

위와 같은 형태를 가지는데(python statsmodels패키지를 이용한 그래프이다), 여기서 e(MEDV|X) 는 반응변수 MEDV를 예측변수 전체(X)로 회귀분석하여 나온 잔차(e)를 의미하고, e(AGE|X)는 변수 AGE를 남은 반응변수(X, AGE 제외)로 회귀분석하여 나온 잔차(e)를 의미한다. 위 plot의 경우는 AGE와 종속변수 MEDV가 상관관계가 없음을 보여주고 있고, 이러한 방식으로 선형모형의 각 변수들에 대한 partial regression을 진행하여 각각의 유의성을 파악할 수 있다.
References
- https://datascienceschool.net/
- The Elements of Statistical Learning