
[743. Network Delay Time]
문제
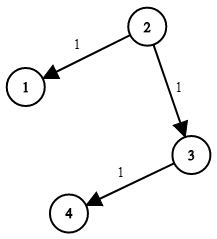
- 노드간 인접 관계와 간선의 가중치를 파라미터로 받고 노드 수, 시작 노드를 받는다.
- 시작 노드에서 부터 모든 노드에 방문하는데 걸리는 최소 시간을 구하는 문제다.(BFS)
- 다익스트라를 활용하는 기본적인 문제다.
- 위 그림에서의 답은 2가 나올 것이다. 4번 노드까지의 거리가 2이기 때문이다.
풀이
-
이 기본문제를 푸는 핵심 포인트는 인접행렬(그래프)를 생성하는 것과 다익스트라 알고리즘을 활용하는 것. 두가지라고 생각한다.
-
우선 인접 정보와 가중치를 List 배열에 해당 노드가 갖는 인접 정보들을 저장해줬다. 참고로 방향이 존재하는 간선이다.
-
위의 예시 그래프가 저장된 정보를 시각화 하면 아래 그림과 같다.
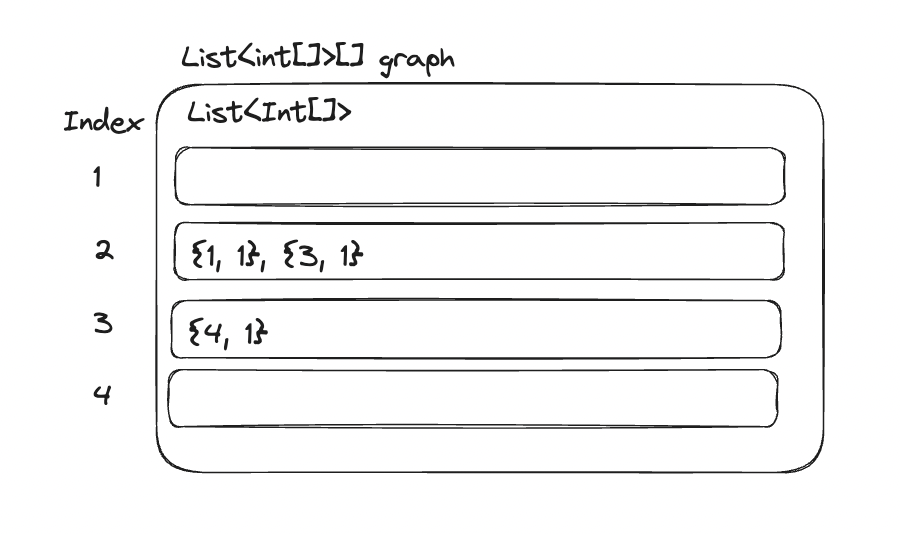
-
2번 노드가 1번, 3번 노드 방향으로 간선이 존재하고 가중치는 각각 1
-
3번 노드가 4번 노드 방향으로 간선이 존재하고 가중치는 1로 존재하게 된다.
-
각 노드간의 최소 거리를 담은 배열 dist[]를 선언하고 출발지를 0으로 초기화 한 후 다익스트라 로직을 돌면 쉽게 풀린다.
다익스트라 기본 개념 : 현재 저장된 목표 노드까지의 거리 > 현재 노드까지의 거리 + 현재 노드에서 목표노드까지의 거리
- 아래 그림을 참고하자.
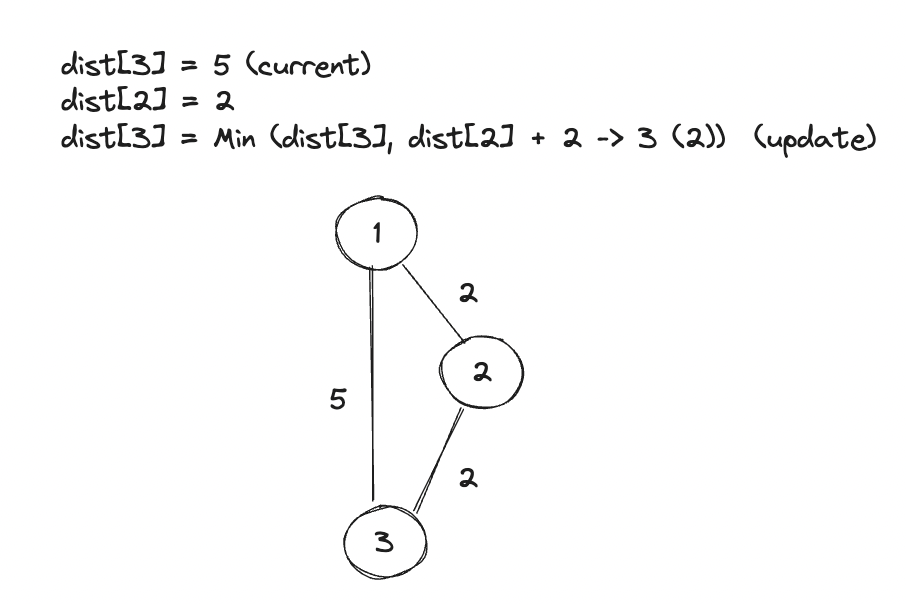
코드
class Solution {
private List<int[]>[] graph;
private int[] dist;
public int networkDelayTime(int[][] times, int n, int k) {
createGraph(n, times);
dijkstra(n, k);
int result = 0;
for (int i = 1 ; i <= n ; i++) {
if (dist[i] == Integer.MAX_VALUE) {
return -1;
}
result = Math.max(result, dist[i]);
}
return result;
}
private void dijkstra(int n, int k) {
dist = new int[n + 1];
Arrays.fill(dist, Integer.MAX_VALUE);
PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> a[1] - b[1]);
dist[k] = 0;
q.offer(new int[] {k, 0});
while (!q.isEmpty()) {
int[] current = q.poll();
for (int[] next : graph[current[0]]) {
if (dist[next[0]] > current[1] + next[1]) {
dist[next[0]] = current[1] + next[1];
q.offer(new int[] {next[0], dist[next[0]]});
}
}
}
}
private void createGraph(int n, int[][] times) {
graph = new List[n + 1];
for (int i = 1 ; i <= n ; i++) {
graph[i] = new ArrayList<>();
}
for (int[] time : times) {
graph[time[0]].add(new int[] {time[1], time[2]});
}
}
}