SCC

SCC(Strongly Connected Component)는 방향 그래프에서 모든 정점이 서로 연결된 부분 그래프를 의미합니다. 즉, 한 SCC 안의 모든 정점 u,v에 대해
u→v (u에서 v로 가는 경로 존재)
v→u (v에서 u로 가는 경로 존재)
이 두 조건을 만족해야 합니다.

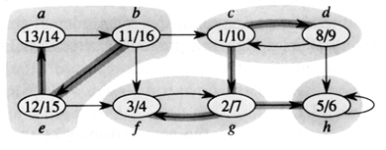
타잔 알고리즘

깊이 우선 탐색 알고리즘(DFS)을 활용해 SCC(Strongly Connected Component, 강한 연결 요소)를 찾는 알고리즘

동작 방식

1. 각 정점을 방문하며 id와 low-link 값을 계산한다.
   low-link란 현재 정점이 속한 SCC에서 가장 낮은 DFS 방문 순서이다.
2. 현재 정점의 id와 low-link 값이 같다면 해당 정점은 SCC의 시작점이다.
3. 스택에서 정점을 꺼내며 SCC를 구성한다.

문제로 확인하기

백준 2150 SCC

전체 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Stack;
import java.util.StringTokenizer;

public class BaekJoon2150 {

    static int V, E, id;
    static boolean[] finished;
    static int[] ids, low;
    static ArrayList<Integer>[] arr;
    static Stack<Integer> stack = new Stack<>();
    static ArrayList<ArrayList<Integer>> sccList = new ArrayList<>(); 

    public static void main(String[] args) throws IOException {
        initialize(); // 그래프 초기화 및 입력 처리
        findSCCs(); // SCC 찾기
        printResult(); // 결과 출력
    }


    private static void initialize() throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        V = Integer.parseInt(st.nextToken()); // 정점의 수
        E = Integer.parseInt(st.nextToken()); // 간선의 수

        finished = new boolean[V + 1]; // SCC 완료 여부
        ids = new int[V + 1]; // 각 정점의 DFS 방문 순서
        low = new int[V + 1]; // 각 정점의 Low-Link 값
        arr = new ArrayList[V + 1]; // 그래프 인접 리스트 초기화
        id = 0; // DFS 방문 순서 초기화

        for (int i = 1; i <= V; i++) {
            arr[i] = new ArrayList<>();
        }

        while (E-- > 0) {
            st = new StringTokenizer(br.readLine());
            int A = Integer.parseInt(st.nextToken());
            int B = Integer.parseInt(st.nextToken());
            arr[A].add(B);
        }
    }


    private static void findSCCs() {
        for (int i = 1; i <= V; i++) {
            if (ids[i] == 0) { // 아직 방문하지 않은 정점이면 DFS 수행
                DFS(i);
            }
        }
    }

  
    private static void printResult() {
        for (ArrayList<Integer> scc : sccList) {
            scc.sort(null);
        }
        sccList.sort((o1, o2) -> o1.get(0) - o2.get(0)); 

        StringBuilder sb = new StringBuilder();
        sb.append(sccList.size()).append("\n"); 
        for (ArrayList<Integer> scc : sccList) {
            for (int node : scc) {
                sb.append(node).append(" ");
            }
            sb.append("-1\n");
        }

        System.out.print(sb);
    }


    private static void DFS(int at) {
        ids[at] = low[at] = ++id; // 현재 정점의 방문 순서와 Low-Link 값 초기화
        stack.push(at); // 스택에 현재 정점 추가

        for (int to : arr[at]) { // 인접 정점 탐색
            if (ids[to] == 0) { // 방문하지 않은 정점이면 DFS 수행
                DFS(to);
                low[at] = Math.min(low[at], low[to]); // DFS 후 Low-Link 값 갱신
            } else if (!finished[to]) { // 방문했지만 아직 SCC로 분리되지 않은 정점
                low[at] = Math.min(low[at], low[to]); // 역방향 간선이므로 Low-Link 값 갱신
            }
        }

        // SCC의 루트 노드인지 확인
        if (ids[at] == low[at]) {
            extractSCC(at); // SCC 추출
        }
    }


    private static void extractSCC(int at) {
        ArrayList<Integer> scc = new ArrayList<>();
        while (true) {
            int node = stack.pop(); // 스택에서 정점 추출
            finished[node] = true; // 해당 정점을 SCC 완료 상태로 설정
            scc.add(node); // SCC 리스트에 추가
            if (node == at) break; // 루트 노드까지 추출하면 종료
        }
        sccList.add(scc); // SCC 결과 리스트에 추가
    }
}