📌 본 논문은?
제목: Interpretable Math Word Problem Solution Generation Via Step-by-step Planning
Team: University of Massachusetts Amherst, Adobe Research
저자: Mengxue Xhang 외
Category : 수학 단어 문제(MWP)
주요 Contribution:
- MWP를 해결하기 위한 solution을 step-by-step으로 생성하기 위해, planning 접근법의 사용을 연구함.
- 높은 해석 가능성(interpretability)과 컨트롤 가능성
- 다양한 downstream task에 대해 적용 가능
- 수학 연산 프롬프트를 바꿈으로써, 같은 문제에 대해서도 다양한 path의 솔루션을 생성할 수 있음.
- 작은 추가 파라미터로도, 기존의 접근법들의 퍼포먼스보다 final answer 정확도와 중간 스텝의 품질을 능가함.
1. Introduction
수학 단어 문제 해결 과제의 중요성과 난점
수학 단어 문제 해결은 자연어 이해와 수학적 지식을 모두 필요로 하기 때문에, 이를 해결하는 것은 인공지능 분야에서 중요한 과제 중 하나이다.
→ 복잡성과 다양성 때문에 문제 해결이 어려움
Prior Works
- Earlier works
- modular approach
-
자연어 해석
-
text pattern을 수식 단어에 맵핑함.
→ 이 접근법은 자연어와 수식 단어 차이를 줄이기 위해 hand-crafted rule에 과도하게 의존하게 됨.
-
- modular approach
- Recent works
- NLP의 발전에 따라, 신경망 기반의 end-to-end approach 채택
- MWP(+ 내포하는 수식)의 수학적인 표현을 인코딩하고, 디코더로 최종 답안을 생성함.
이전 연구들의 단점
- 주로 최종 답안 생성에 초점을 맞추어 왔으며, 중간 solution step의 품질에 대한 연구는 부족했음.
최근 연구들
- final answer뿐만 아니라, intermediate steps(풀이 과정)을 함께 생성하는 방법으로 바뀜.
- 반면, 현존하는 LM들은 잘못된 intermediate steps를 생성할 가능성이 있다. (final answer는 맞지만, 중간 과정 틀리는 경우 존재)
→ 본 논문: 이러한 문제를 해결하기 위해, 중간 솔루션 단계의 품질을 개선하는 방법론 제안
= 계획 기반 언어 모델링(Planning-based language modeling)
데이터셋
GSM8K : 2~8개의 intermediate step을 가지고 있는 MWP이고, 자연어로 기술됨.
많은 연구들이 LM을 적용해 final answer 생성에 대해 높은 정확도를 달성했다. (중간 과정 생성 학습은 x)
→ 이 연구들은 verifiers, self-consistency decoding strategy(majority votes), chain-of-thought prompting, or calculators를 사용했다고 함.
1.1 Contributions
-
MWP를 해결하기 위한 solution을 step-by-step으로 생성하기 위해, planning 접근법의 사용을 연구함.
→ 본 논문에서는, 먼저 높은 품질의 중간 solution step을 LM을 통해 생성하는 것에 집중한다고 하고 있음.
-
a. 다음 solution step에 사용될 수학적인 수식을 small model을 이용해서 예측함.
- carefully-constructed prompt 적용하여, LM이 다음 solution step을 생성할 수 있도록 함.
→ 이 접근법은 다양한 downstream applications에 적용될 수 있다.
→ 해석 가능성(interpretability)과 컨트롤 가능성이 높기 때문
-
작은 추가 파라미터로도, 기존의 접근법들의 퍼포먼스보다 final answer 정확도와 중간 스텝의 품질을 능가했다고 함.
또한, 수학 연산 프롬프트를 바꿈으로써, 본 논문의 접근법을 컨트롤하여 같은 문제에 대해서도 different correct solution paths를 생성할 수 있다고 함.
1.2 Notation
2. Methodology
task: Question Q가 주어졌을 때, step-by-step solution S = S1, S2, … 를 생성해야 함.
각각의 step은 text와 mathematical tokens이 합쳐진 형태로 이루어져 있음.
문제를 프롬프트 기반의 LM을 fine-tuning해서 step-wise controllable generation task로 나타냄.
본 논문에서 제안하는 접근법에는 2가지의 main component가 있음.
2가지 main component
- MWP와 solution history를 사용하여, 다음에 나와야 할 수학적인 연산을 plan하고 predict하여 다음 스텝에 적용할 수 있도록 함.
- 다음 step 생성 과정을 guide할 수 있도록, instruction prompt와 함께 예측된 연산 프롬프트를 사용함.
Key technical challenges
- how to learn a solution planning strategy to transition from step to step
- once we have next operation, how to apply and design prompts to guide the generative LM to generate the next step to follow the plan.
2.1 Operation Prediction
Notation
vocabulary embedding function a separate prompt embedding function parameter weight 𝑠 ∈ $[0, 1] ^ { O $ O ɣ the set of parameters for the classifier the score of operation class an indicator such that when == true label, otherwise 0
첫 번째 스텝: 다음 스텝에 적용될 수학적인 연산을 예측하는 것.
→ 실현 방법: solution history H ⊕ craft instruction prompt P (예: “What is the next operation?”)
- 프롬프트를 LM의 input으로 하여 얻은 Special token “[cls]” 를 concat함. (LM의 size는 클 필요가 없다고 함.)
- H(Solution history) token은 로, P(instruction prompt) token은 로 encode함.
- H(Solution history)의 표현을 얻음. (LM의 마지막 layer의 hidden state)
다음 스텝의 연산 action을 예측하기 위해서,
Classifier과 같은 하나의 fully-connected network 레이어를 사용함. (with weight )
→ s 얻음 (각각의 수학 연산에 대한 연산 스코어 벡터)
Language Model의 사용
Step 생성하기 위해 LM을 사용해야 함.
연산 예측을 위해 별도의 LM을 도입하면 많은 파라미터가 생성됨.
→ 그러므로, 같은 LM을 Operation planning과 Solution step generation 모두 사용함.
Loss function
Operation planning 과 Solution step generation 모두 cross-entropy loss 사용함.
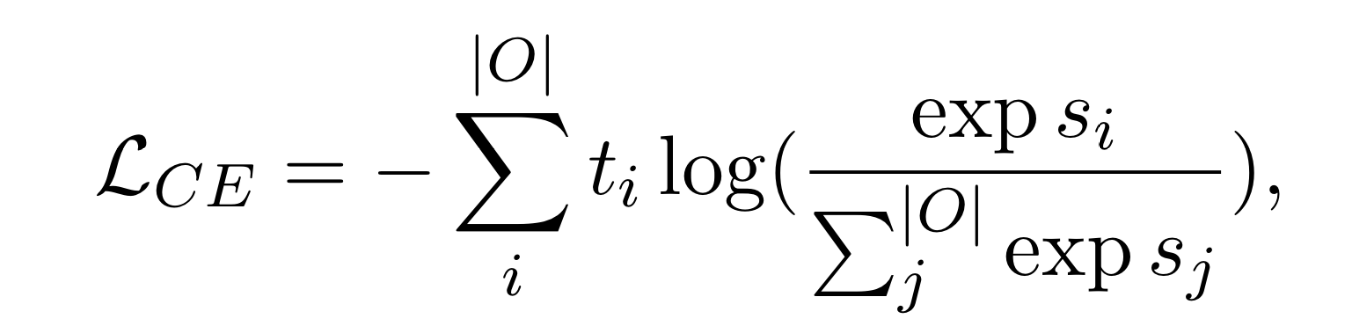
true label
training data 안의 solution의 각 스텝에서 추출하여 true label을 얻어옴.
2.2 Controllable Step Generation
일단 예측된 연산 가 주어졌다고 하면, 그에 알맞는 prompt를 instruction prompt 에 append함.
→ Step generation을 위한 final prompt 형성
task가 컨트롤 가능한(controllable) Generation Task가 된다
: 히스토리 와 다음 step을 예측하는 프롬프트 가 주어졌을 때,
목표는 다음 step 를 토큰 단위로 생성하는 것.
다음과 같이 step 생성
(다음과 같이 주어졌을 때.)
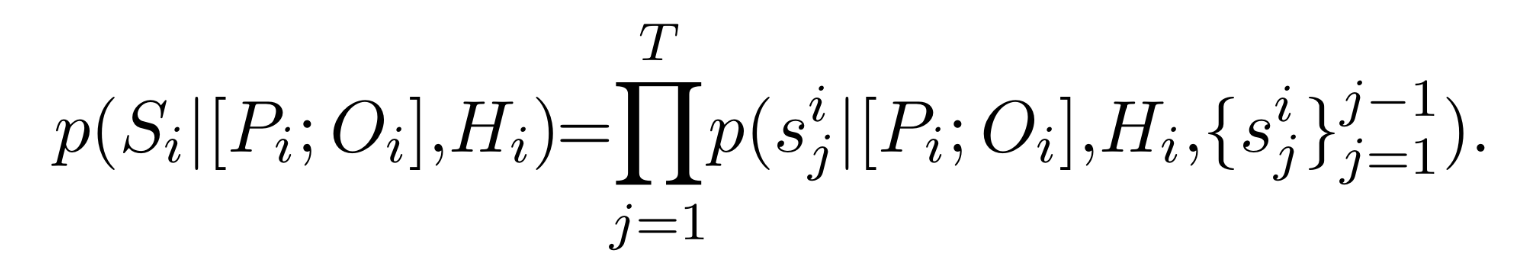
Then, the overall step-by-step solution S with N steps is generated according to
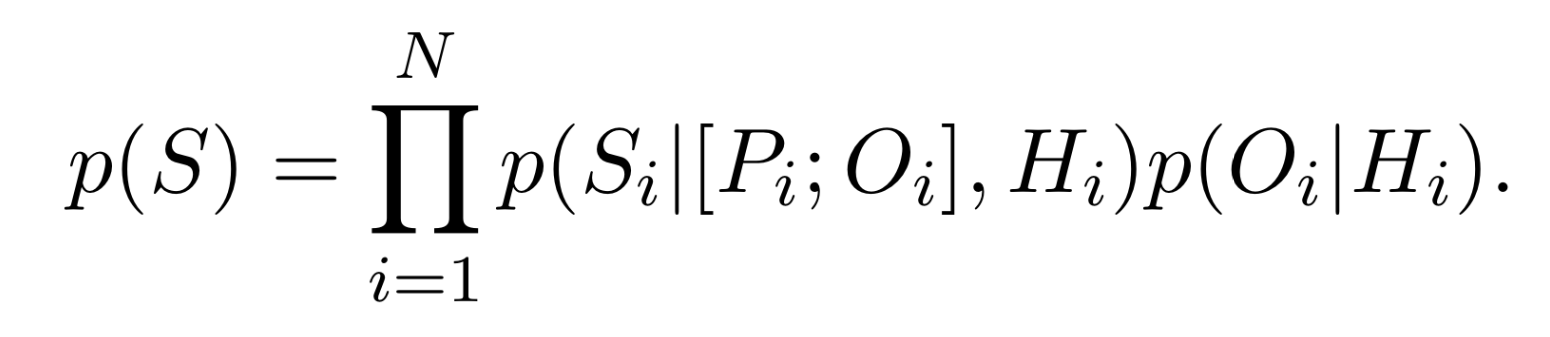
Step Generation의 loss function
: log-likelihood objective function
Notation
| LM parameters | |
|---|---|
| LM parameters |
Prompt Position
: LM에 넣을 프롬프트의 위치를 2가지로 나누어 실험하였음.
-
as prefix
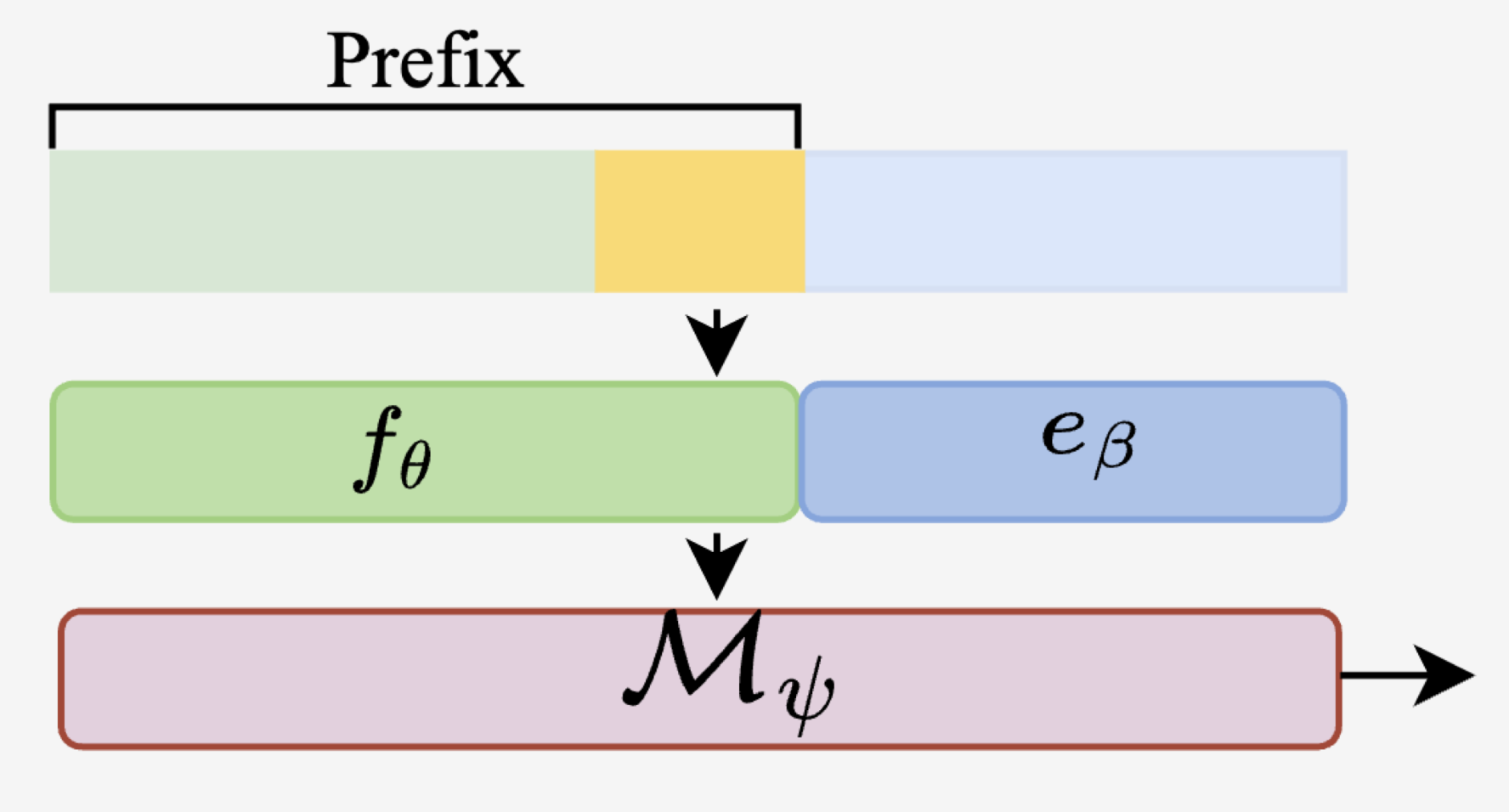
- where we place them at the beginning
- input 예시)
-
as infix
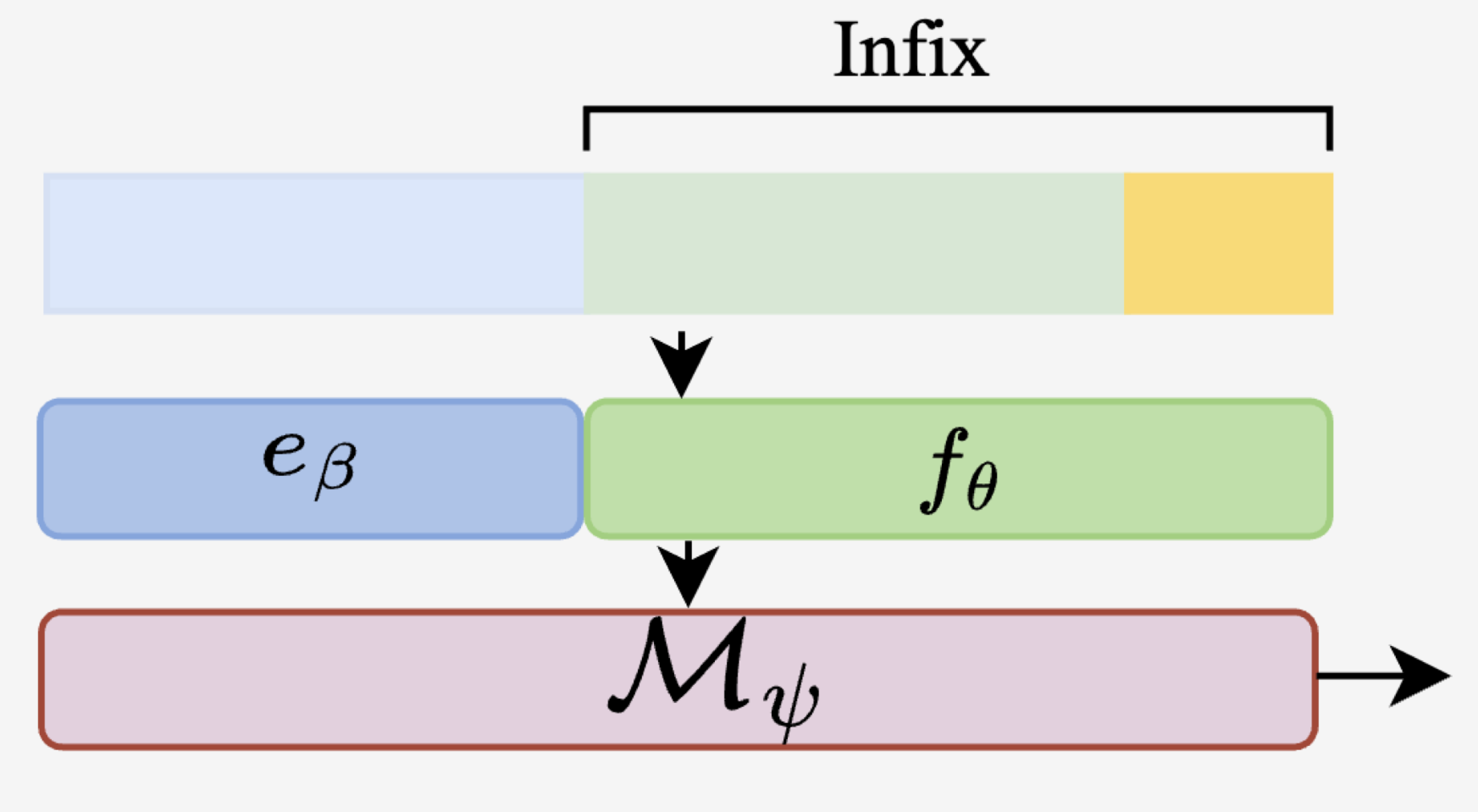
- where we append the prompt after the history
- input 예시)
2.3 Prompt Design
✔️ 프롬프트는 2개의 파트로 나뉘어짐
- Instruction prompt
- 무엇을 생성할지에 대한 general instruction을 LM에 제공
- prompt mining 적용하여, 좋은 instruction을 찾음.
- i.e.) word tokens that are the most informative for the LM to accomplish the desired task.
- Section D.2) Prompt mining through paraphrasing Step 1. seed prompt로부터 시작, 이것을 paraphrasing함으로써 prompt mining함.
-
seed prompt 예시) “The next step operation is: “
Step 2. 비슷한 의미를 지닌 다른 candidate prompts로 paraphrase함.
Step 3. candidates를 hyper-parameters로 간주하여 모델을 튜닝함.
→ target task에서 가장 좋은 성능을 내는 프롬프트를 선택함
그 결과, “?”와 같은 물음표(anchor tokens)가 좋은 성능을 낸다는 것을 발견함.
(선행연구(Liu et al., 2021c) 와 비슷한 결과)
-
- Operation prompt
- 다음 스텝에 수행될 연산에 대한 specific한 가이드라인을 제공함.
- training data로부터 자주 나타난는 20개의 연산을 추출함
- 예) one step의 연산
- addition , substraction , multiplication , …
- 이것들을 프롬프트로 사용
- 예) one step의 연산
- 이러한 연산자들은 쉽게 찾아낼 수 있고 자동으로 추출할 수 있다. → 따라서, Operation prediction LM을 training하기 위해 label을 수동으로 생성할 필요 없음.
✔️ instruction 토큰과 operation 토큰이 전체 Prompt function 의 전체 단어를 형성함.
- instruction tokens and operation tokens form the entire vocabulary of the prompt function .
✔️ Prompt function: 2-layer perceptron with a ReLU activation function.
2.4 Optimization
-
Although our entire approach can be trained together in an end-to-end way, we found that optimizing the operation prediction model and fine-tuning the LM/prompts for step generation asynchronously leads to better performance.
-
전체 접근법은 end-to-end 방식으로 함께 training 될 수 있지만, 그것보다는
Operation prediction model을 최적화하고
step generation에 대한 LM/prompts를 비동기적으로 fine-tuning하면 성능이 더 향상되었다.
💡 직관(예상)
| Operation predictor | LM Generation process | |
|---|---|---|
| 대상 | 전체 solution | 현재의 step에 대해서만 |
| level | high-level | low-level |
-
Operation predictor
- 전체 solution에 대해
- high-level의 결정을 내리는 policy
-
LM Generation process
- 현재의 step에 대해서
- low-level (token-by-token)의 결정을 내리는 프로세스
- 두 모듈을 동시에 최적화하면 불일치(inconsistency)를 유발할 수 있음. : Operation predictor가 업데이트가 필요한 LM의 파라미터를 기반으로 결과값을 낼 수 있기 때문.
→ 그러므로,
-
학습 데이터에서 각 스텝의 mathematical part에서 추출한 ground-truth 연산 label을 사용
→ step generation task의 loss와 함께 생성 모델과 프롬프트의 파라미터 최적화
-
모델 M과 prompt fuction f를 모두 freezing하는 것과, Operation predictor를 튜닝하는 것을 switch 반복함.
→ 이러한 방법으로 전체 모델을 안정적으로 수렴하는 것을 보장함.
3. Experiments
데이터셋
-
GSM8K
- 언어적으로 다양한 MWP
- size: 8.5K
- 중간 solution step: 2~8개 정도
-
Preprocessing
- Section C. 참고
3.1 Automated Metrics
- solve rate
- metric to evaluate whether the model generates the final correct answer to each MWP
- BLEU
- evaluate language generation quality
- ACC-eq
- For intermediate steps, use the equation match accuracy metric to evaluate whether a generated step contains a math expression (including numbers) that matches the ground truth.
- Since LMs generate math equations as strings, → we decompose the equation string into tokens and calculate the token level match rate instead of the overall string match.
- ACC-op
- We also use the operation match accuracy metric to evaluate whether a generated step’s operation label matches the ground truth.
3.2 Human Evaluation
- BLEU와 같은 텍스트 유사도 평가 지표는 중간 솔루션 단계의 수학적 타당성을 정확하게 반영하지 않음. → 따라서, 자동화된 메트릭만을 사용하여 제안된 planning-LM 프레임워크를 정확하게 평가할 수 없음.
- 이러한 한계를 해결하기 위해 아래 세 가지 메트릭으로 Human Evaluation 프로토콜을 구현함.
- reasoning strategy
- clear explanation
- overall preference
- 기본 수학 개념에 대한 이해도가 높은 10명의 평가자는 프로토콜을 사용하여 무작위로 선택된 50개의 MWP를 평가함. (Google form을 통해 수집)
- task?
- 랜덤으로 할당된 step-by-step solutions A, B를 비교하는 것 : Chain-Of-Thought vs. Planning-LM
- The full evaluation template
- Section G.
- Figure 4.
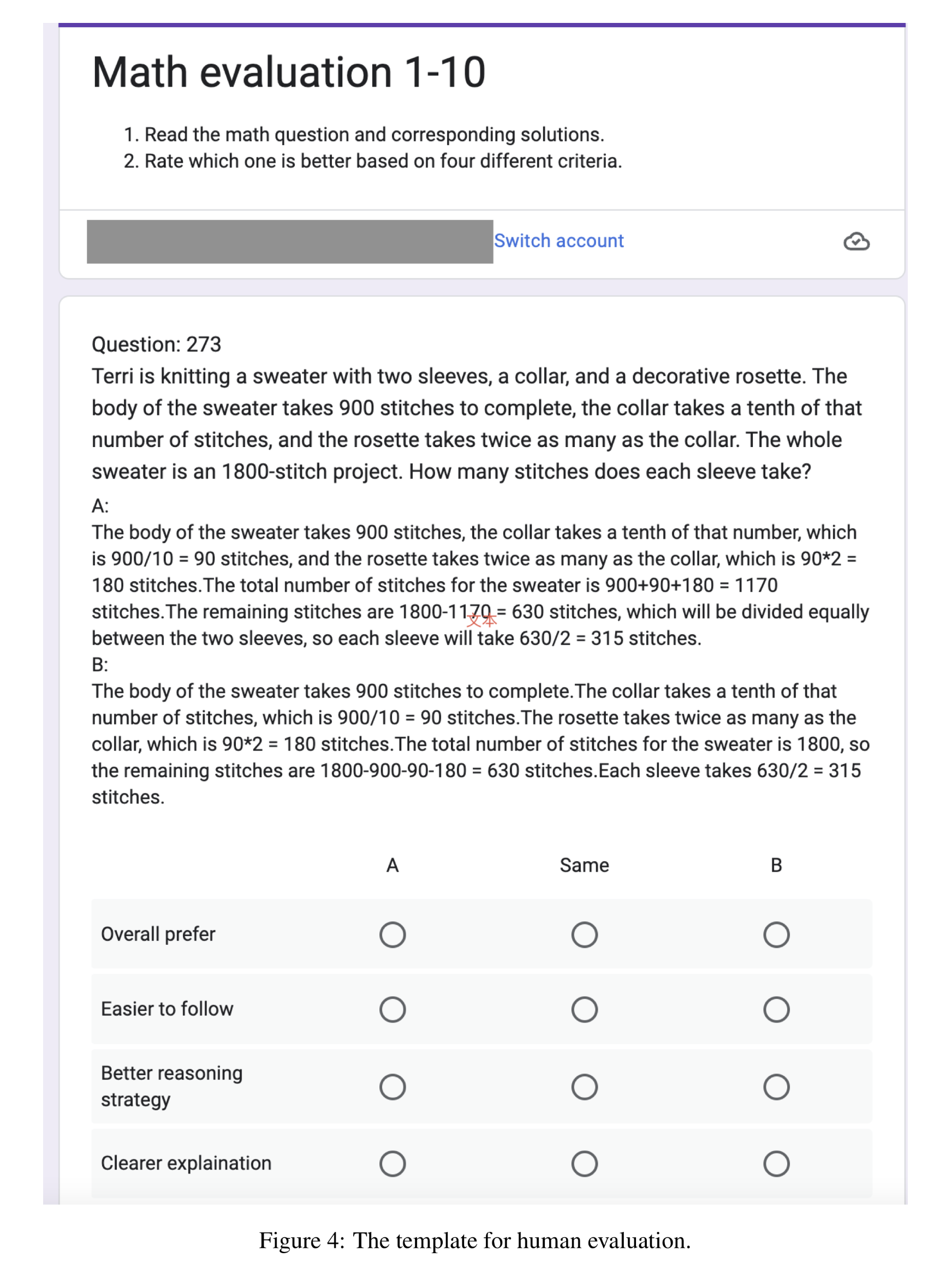
- Figure 4.
- Section G.
- 랜덤으로 할당된 step-by-step solutions A, B를 비교하는 것 : Chain-Of-Thought vs. Planning-LM
- task?
3.3 Experimental Settings
2가지 실험 수행 → planning-LM의 framework의 유효성(effectiveness) 확인
-
Single-step experiment
-
모델에 Question과 Ground-truth solution step을 input으로 제공, 다음 step을 생성하게 하는 실험.
-
평가 지표: ACC-eq와 ACC-op를 각각의 생성된 스텝에 대해 계산하게 함.
-
Step의 일부는 너무 짧기 때문에, BLEU score의 높은 분산을 유발할 수 있음.
→ 생성된 모든 스텝을 concat하고,
BLEU score을 처음부터 끝까지의 히스토리와 솔루션 사이에 대해 계산함.
-
-
All-step experiment
- 모델에 MWP만 input으로 제공, 모든 solution steps을 생성하게 하는 실험.
- 평가 지표: solve rate metric 계산하여, 최종 답안이 맞았는지 평가함.
- base model: GPT-2 (117M parameters) and GPT-2 medium (345M)
- LM fine-tuning과 planning-LM의 생성 결과를 비교함
- Another experiment
- ground-truth operation prompt를 input으로 사용해 planning-LM이 다음 스텝을 생성하도록 함.
- The result, an upper bound on the performance of planning-LM, reflects the effectiveness of low-level token-by-token generation in each step, while ACC-eq and ACC-op reflect the effectiveness of high-level mathematical operation planning across steps.
- We also conduct the above experiments on encoder-decoder LMs : T5-base(220M), T5-large(770M)
- Decoder architecture is the same as GPT-2 models, but instead of treating the question as history input, T5 contains an extra encoder to encode the question and uses cross attention to the question to generate results.
-
한편, we perform another experiment using the ground truth operation prompt as input for planning-LM to generate the next step
-
LLM prompting에 관한 다른 연구들(예: chain-of-thought)과의 공정한 비교를 위해,
상대적으로 작은 LM에 prompt-tuning을 하지 않고,
planning-LM에 in-context learning (few-shot, zero-shot)을 적용하였다.
-
다음과 같은 형태로 5개의 샘플 선택
- (Prompt-Operation-Solution) 세 쌍이 반복하여 나오는 형태
- 이 샘플로 GPT-3(”text-davinci-003”)으로 in-context learning 수행함
- table 6.

- (Prompt-Operation-Solution) 세 쌍이 반복하여 나오는 형태
3.4 Quantitative Results
3.4.1 Prompt tuning
4가지 평가지표 결과 비교
2개의 실험에 대해 모든 prompt-tuning 결과는 다음과 같이 도출됨.
Table 1.
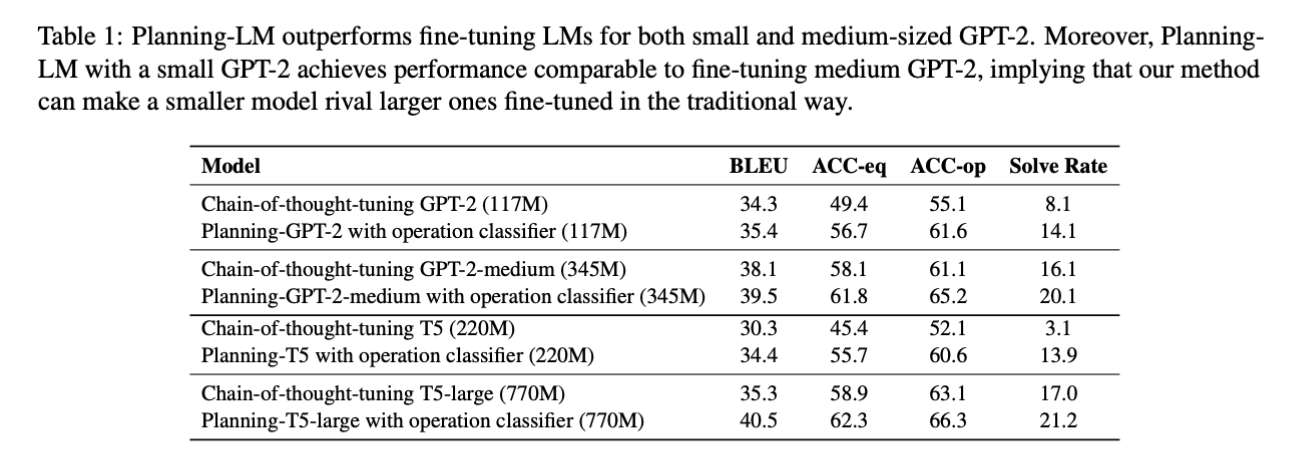
🔎 결과 분석
-
GPT-2와 T5 모두, operation classifier + planning-LM을 적용한 것이 chain-of-thought-tuning을 적용한 것보다 더 우수한 결과를 보였음.
-
유사한 경향이 더 큰 모델인 GPT-2-medium 및 T5-large에서도 유지됨.
-
planning component (약 10K parameters)를 통해, 훨씬 큰 모델에 대해서도 유사한 결과
GPT-2 (base, 117M parameters) ↔︎ GPT-2 (medium, 345M parameters)
→ 거의 유사한 결과 나왔다는 것을 강조함.
- MWP 해결 task에 대해, 높은 parameter-efficient를 보여준다고 강조함. (즉, 적은 파라미터로도 좋은 결과 얻을 수 있다)
- The other observation is that our approach seems to adapt better to decoder-only LMs than to encoder-decoder LMs,
even ones with more parameters;
T5-base yields almost the same performance as GPT-2, with twice as many parameters.
- 본 논문에서 주장하는 방법론이, 파라미터가 더 많은 경우에서도 encoder-decoder LM들보다 decoder-only LM이 더 적용시키기 쉬웠다고 함.
- T5-base ≈ GPT-2 : parameter 수가 2배 정도 차이나는 T5-base와 GPT-2를 비교해도 결과가 거의 비슷했음
- T5-base ≈ GPT-2 : parameter 수가 2배 정도 차이나는 T5-base와 GPT-2를 비교해도 결과가 거의 비슷했음
Ablation Study
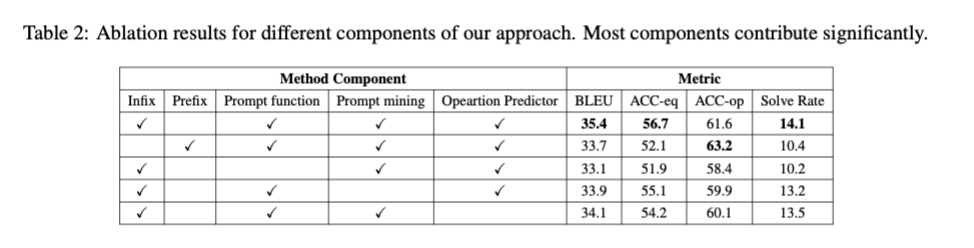
-
planning-LM approach의 4가지의 컴포넌트에 대해 ablation study 진행
- prefix or infix prompts
- fixed or fine-tuned mathematical operation prompts
- instruction prompt mining
- operation predictor
-
결과
- infix + fine-tuned 연산 프롬프트 + 연산 예측기 의 조합이 가장 성능을 높였음.
- 선행 연구 결과와는 다르게, prefix보다 infix prompt를 사용하는 것이 성능을 비약적으로 상승시켰음. → Possible explanation:
- Prefix prompting과 Step-by-step Generation의 성격이 상반됨(incompatibility)
- prefix prompts는 LM input의 맨 앞에 가장 중요한 instruction을 배치함 → 모든 토큰이 LM input에 참여하도록 하여, operation prediction accuracy는 높으나 다른 토큰들에 대해서는 생성 성능이 저하됨. → 이거 당최뭔소린지
- prefix prompts는 LM input의 맨 앞에 가장 중요한 instruction을 배치함 → 모든 토큰이 LM input에 참여하도록 하여, operation prediction accuracy는 높으나 다른 토큰들에 대해서는 생성 성능이 저하됨. → 이거 당최뭔소린지
- Prefix prompting과 Step-by-step Generation의 성격이 상반됨(incompatibility)
3.4.2 In-context learning
-
GPT-3에게 다양한 포맷의 in-context prompting example를 제공하는 실험 결과
-
결과: Table 3.
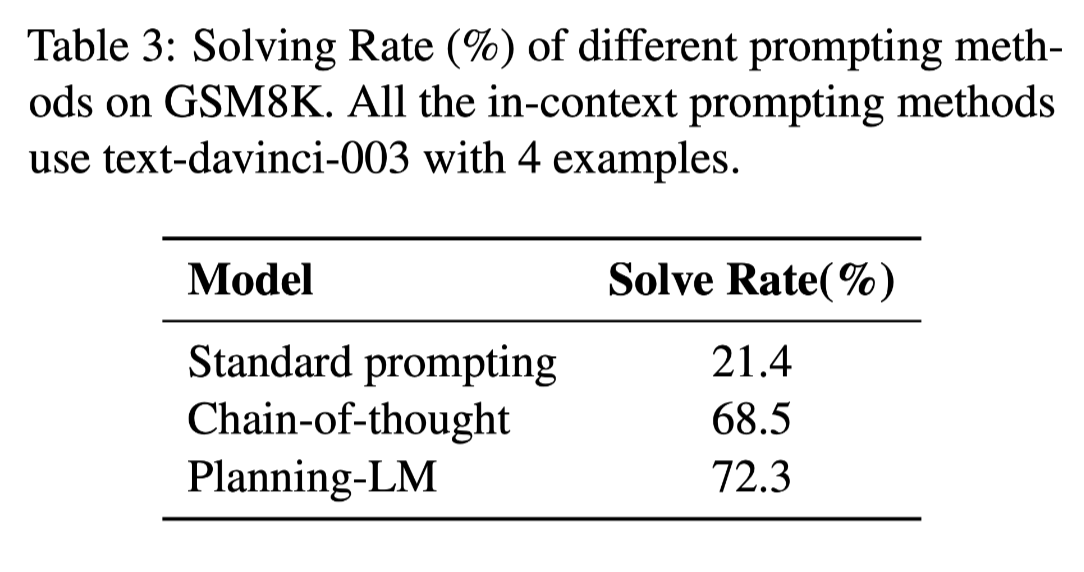
→ 다른 접근법들보다, Planning-LM이 훨씬 더 높은 성능을 보였음.
3.5 Human Evaluation Results
- 결과: Figure 2
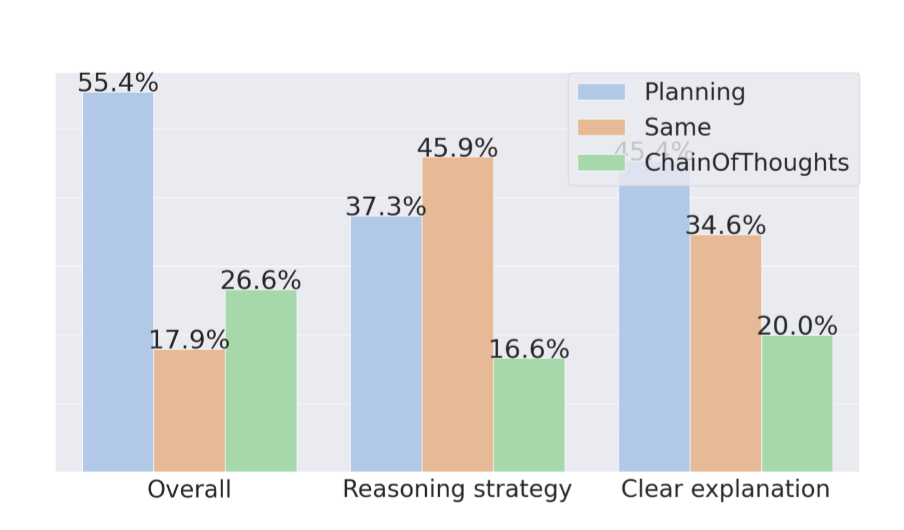
- 같거나 더 우수하다는 답변 결과를 보여줌3.6 Qualitative Analysis
-
Full step-by-step solution 비교 (Planning-LM vs. Chain-of-thought prompting)

- 1번 예시에 대해,

- **Chain-of-thought**
- 처음에는 올바른 풀이과정을 내놓았으나, 3번째 풀이과정부터 틀린 풀이를 생성했음.
- 그럼에도 불구하고 “Round to the nearest integer”라는 지문이 문제에 있어서 이 과정을 수행한 후 나온 최종 답은 맞게 됨. (그 전 과정의 답인 1.33은 틀렸음.)
- **PlanningLM**
- 올바른 풀이와 올바른 답 도출함- 2번 예시에 대해,

- **Chain-of-thought**
- 디테일한 단어를 사용하지 않음.
- **Planning-LM**
- 해설의 각 step에 디테일한 단어를 사용하여, 훨씬 더 이해하기 쉽도록 하였음.- 다음 step에서 다른 수학 연산을 예측한다면, 여러 해를 생성할 수 있다는 것 발견함.
→ 모델이 대안적인 올바른 해 전략을 생성할 수 있는지 보기 위해,
Operation prompt를 통해 handcrafted plan을 제공하여 후속 실험을 수행

Plans I and II
- enables the model to generate the correct final answer among the four strategies we used;
- the generated solutions follow the operation steps given, indicating that the model has some reasoning ability and can extract some meaningful patterns from data.
Plan III
- results in a flawed solution
Plan IV
- failed
- since we do not have an operation class that matched the step.
- For plan III, the first step, [n + n + . . .], is not seen often enough in the training data.
- For plan IV, (n + n) × n is not seen in the training data either.
- 이 경우, 가장 비슷한 연산 [n + n × n]을 사용하면 정확한 최종 답변에 매우 가까운 결과를 얻을 수 있다는 것을 알 수 있음. → 이러한 결과는 현재 접근 방식이 미리 정의된 유한한 연산의 수로 제한되어 있기 때문에, Operation Prompt의 더 나은 표현이 미래 작업에 중요하다는 것을 나타냄.
- classifier 대신 prompt operation generator가 수학적 연산의 다양한 유형의 해설을 생성하기 위해 더 좋은 선택일 수 있음.
- 이 경우, 가장 비슷한 연산 [n + n × n]을 사용하면 정확한 최종 답변에 매우 가까운 결과를 얻을 수 있다는 것을 알 수 있음. → 이러한 결과는 현재 접근 방식이 미리 정의된 유한한 연산의 수로 제한되어 있기 때문에, Operation Prompt의 더 나은 표현이 미래 작업에 중요하다는 것을 나타냄.
4. Related Works
: 수학 단어 문제 해결과 관련된 이전 연구들
1. 기계 학습 기반 방법론
- 수학 단어 문제를 자연어 처리 문제로 취급하고, 기계 학습 기반 모델을 사용하여 최종 답안을 생성함.
- 최종 답안 생성에 초점을 맞춤. → 중간 솔루션 단계의 품질에 대한 연구는 부족했음.
2. 계획 기반 방법론
- 수학 단어 문제를 계획(plan)으로 변환하고, 계획을 수행하는 과정에서 중간 솔루션 단계를 생성함.
- 중간 솔루션 단계의 품질을 개선하는 데 초점을 맞춤 → 최종 답안 생성에 대한 연구는 부족했음.
본 연구
각각의 방법론에서 사용된 기술들을 참고하여, 계획 기반 방법론과 기계 학습 기반 방법론을 결합하여 중간 솔루션 단계의 품질을 개선하는 방법론을 제안함.
문제 정의
Math Word Problems (MWPs) : 수학 단어 문제 해결 과제
다음과 같이 정의함.
- fine-grained
- step-by-step controllable solution generation
Method
계획 기반 언어 모델링(Planning-based language modeling) 기반.
제안하는 방법론은 다음과 같은 과정으로 이루어짐.
- 입력으로 주어진 수학 단어 문제를 계획으로 변환함.
- 계획을 수행하는 과정에서 필요한 중간 솔루션 단계를 생성함.
- 생성된 중간 솔루션 단계를 이용하여 최종 답안을 생성함.
중간 솔루션 단계를 생성하는 과정에서는 다음과 같은 방법을 사용함.
- 이전 솔루션 단계와 수학적 지식을 이용하여, 다음 솔루션 단계에서 필요한 수학 연산을 예측함.
- 예측된 수학 연산을 이용하여, 다음 솔루션 단계를 생성함.
이러한 방식으로 중간 솔루션 단계를 생성하면서, 계획 기반 방법론과 언어 모델링 기반 방법론을 결합하여
→ 중간 솔루션 단계의 품질을 개선하고, 최종 답안의 정확성을 향상시킨다고 주장함.
Conclusion
본 논문에서는 자연어로 이루어진 수학 문제에 대해 더 세밀하고, 단계별로 제어할 수 있는 해설 생성하는 문제를 제기함.
-
Planning과 Langage Model을 결합시켜, solution step들을 생성하는 방법을 제안함.
-
제안하는 방법론은 PLM(Pre-trained Language Model)을 2가지 방법으로 이용함
각 스텝에서,
- 적용될 수학 연산을 plan
- 1에서 생성한 plan을 prompt로 사용해, 각 스텝에서의 token-by-token 생성 컨트롤
-
작은 추가 파라미터를 추가하는 것을 통해, fine-tuning된 Language model의 문제 풀이 성능을 훨씬 능가하는 것을 증명함.
-
해석 가능성과 높은 제어 가능성 덕분에,
다른 solution plan을 제공하면 한 가지 질문에 대해서도 다양한 해설(alternative strategies)을 생성할 수 있음을 보여줌.
- Future work: 각 단계에 대한 수학 연산자 예측하고 각 단계를 생성한 후, 계획을 수정해 전체 해설 path를 생성하는 것을 더 연구해볼 수 있음.
