[논리회로] Boolean Algebra

Axioms of Boolean Algebra

• set of elements B
• {+}, {$\cdot$}, {'} 세 가지 연산이 존재
• 아래의 Axioms를 만족 -> B와 세 가지 연산은 Boolean algebra를 구성한다.

1. B는 적어도 두 개의 서로 다른 원소 a, b를 포함한다.
2. Closure
   For every a, b in B,
   a. a + b is in B
   b. a $\cdot$ b is in B
3. Commutative laws
   For every a, b in B,
   a. a + b = b + a
   b. a $\cdot$ b = b $\cdot$ a
4. Associative laws
   For every a, b, c in B,
   a. (a + b) + c = a + (b + c) = a + b + c
   b. (a $\cdot$ b) $\cdot$ c = a $\cdot$ (b $\cdot$ c) = a $\cdot$ b $\cdot$ c
5. Identities
   a. There exists an identity element WRT {+}, designated by 0, such that a + 0 = a for every a in B.
   b. There exists an identity element WRT {$\cdot$}, designated by 1, such that a $\cdot$ 1 = a for every a in B.
6. Distributive laws
   For every a, b, c in B,
   a. a + (b $\cdot$ c) = (a + b) $\cdot$ (a + c)
   b. a $\cdot$ (b + c) = (a $\cdot$ b) + (a $\cdot$ c)
7. Complement
   For each a in B, there exists an element a' in B (the complement of a) such that
   a. a + a' = 1
   b. a $\cdot$ a' = 0

• set B = {0, 1}과 logical operations AND, OR, NOT이 Boolean algebra의 모든 axiom을 만족하기 때문에, Boolean algebra로 표현이 가능하다.
• Boolean function : input {0, 1} 을 output {0, 1}로 uniquely 대응시킨다. -> 결국 truth table로 표현 가능 -> 앞서서 썼던 방법인 truth table to boolean expressions 방법을 사용 가능하다.(Sum of Products 방법) -> 모든 Boolean function은 AND, OR, NOT연산으로 만들 수 있다.

Theorems of Boolean Algebra

• duality
  • AND operation과 OR operation을 서로 교체
  • 0은 1로, 1은 0으로 교체
  • Boolean expression으로 true인 어떤 statement도 Dual에서는 true이다.
  • ex) $(X + 0 = X)^D = (X \cdot 1 = X)$
  • 증명을 찾아보면 결국 AND operator를 OR operator로 바꾸고, 1과 0을 서로 바꾸게 된 B, +, $\cdot$도 또한 Boolean Algebra를 만족하므로 Boolean Algebra를 통해 항상 참임이 증명된 명제는 당연히 Dual또한 항상 참이 될 수 밖에 없다.
• Theorems
  
  

Realizing Boolean Formulas

Logic Gates

• 같은 하나의 연산일지라도 필요한 switch 수, wire수, 등등이 다 다르다.
• 예를 들면, NAND와 NOR의 경우 직관적으로 잘 와닿지는 않지만, AND와 OR보다 더 적은 switch를 필요로 하기에 실제로 더 많이 사용된다.

Logic Blocks and Hierarchy

• Two-bit-adder function 구현하기
  
  
  

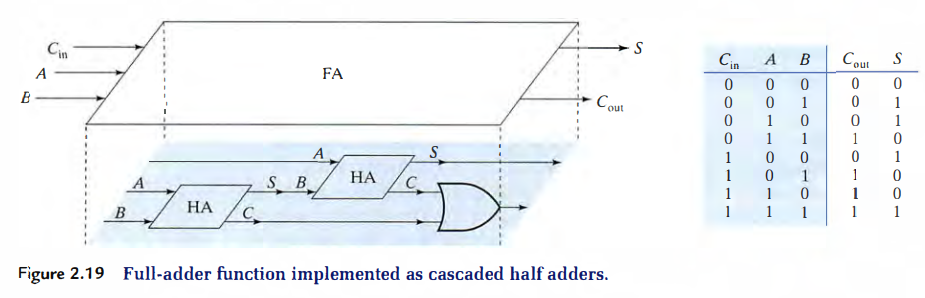
Time Behavior and Waveforms

• 각 gate마다 delay가 존재하고, 이는 각자 다르다.
• ex) AND gate의 경우 NAND gate + NOT gate로 이루어져 있고, 이를 통해 약간 느리다는 것을 알 수 있다.
• 지연이 존재하기 때문에 아주 짧은 시간동안 값이 튈 수도 있고, 이는 무시해야 한다.

Minimizing the Number of Gates and Wires

• Time and Space Trade-Offs - metric을 계산하는 3가지 방법
  1. Boolean function의 literal의 수 세기
     • transistor의 수, wire의 수를 근사적으로 세는 방법.
     • input의 양에는 한계가 있다. (보통 2 ~ 4정도)
  2. gate의 수 세기.
     • circuit의 area를 고려하는 방법.
     • 가장 간단한 디자인 : fewest gates 사용.
     • 기술이 좋아지면서 사이즈가 작아지기 때문에 중요도가 점점 떨어지는 중.
     • wire의 공간차지 또한 고려해야 한다.
  3. gate의 cascaded level
     • logic level이 높아질 수록 delay가 길어지게 된다, but minimum delay를 구현하기 위해서는 앞에서 제시했던 조건들을 만족시키지 못하게 됨.

Two-level Logic

Canonical(표준이 되는) Forms

• 특정한 Boolean function에 대해서 Canonical form을 정할 것임.
  • Sum-of-Products(disjunctive normal form / minterm expansion)
    • minterm : ABC, AB'C, 등등 모든 variable이 딱 한 번씩만 나온다.
    • truth table에 의해 unique하게 결정된다.
      
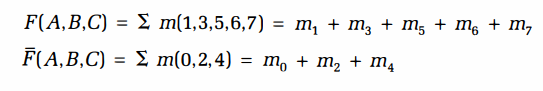
    • 위와 같이 표현하기도 한다.
  • Product-of-Sums(conjunctive normal form / maxterm expansion)
    • maxterm : minterm과 유사, 형태는 A + B + C처럼 ORed Sum에 해당한다.
    • truth table에 의해 unique하게 결정된다.
    • SOP 처럼 각 결과가 0이 나오는 row를 찾아서 0인 variable은 그대로, 1인 variable은 complement를 취해서 OR 연산을 하게 되면 해당 row만 0, 나머지 row는 1이 된다. 이런 방식으로 모든 0 row에 대해 찾아낸 maxterm끼리 AND 연산을 해 주면 된다.
      
    • 마찬가지로 위와 같이 표현하기도 한다.
  • Maxterm expansion은 Minterm expansion의 complement를 다시 complement 연산을 해서 DeMorgan's law를 적용하면 유도된다. 물론 반대방향도 가능.
  • minimized SOP는 minimized POS로 전환 가능하다.(Complement 2번 적용, DeMorgan's law 사용)
• Conversion between Canonical Forms
  

Incompletely Specified Functions

• 말 그대로 함수가 완전히 정의되지 않은 형태이다.
• 특정한 입력에 대해서는 어떠한 값이 결과로 나오든 상관 없다는 뜻.
• don't care이라고도 부르고, undefined나 don't know와는 구분된다.
• 더 효율적인 회로를 구성하기 위해 don't care값을 임의로 정할 수 있다.
  
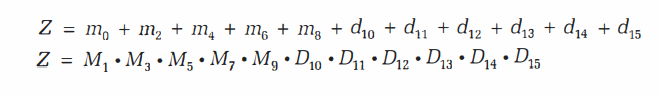
• canonical form은 위와 같이 나타낸다.

Motivation for Two-Level Simplification

• 지금까지의 방법의 단점: minimum solution인지 판별할 수 있는 알고리즘이 없다..!
• Boolean cube & Karnaugh map 배울 예정.

Graphing Boolean Expressions

• 연속함수 x = y의 그래프를 2차원 평면에 나타내듯, Boolean function 또한 이산적인 점들을 통해 그래프로 나타낼 수 있다.
  

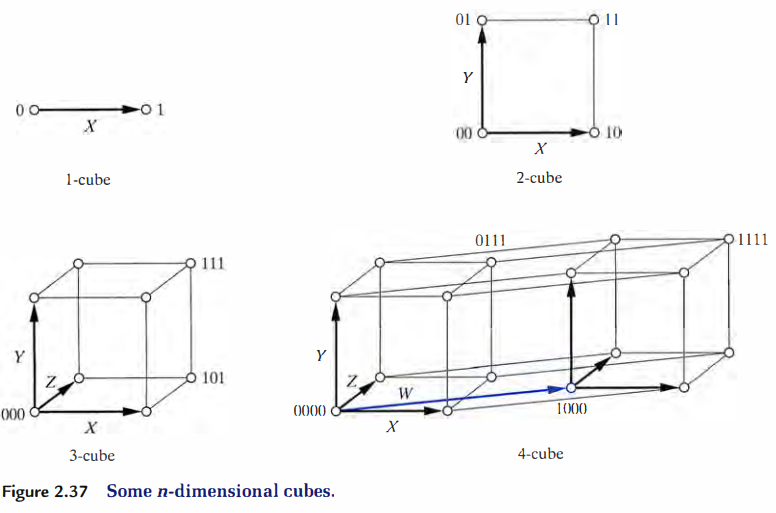
Boolean Cubes

• 이산적인 점들은 cube를 통해서 나타낼 수 있다.
• 각 변수는 하나의 축에 해당함.
• 4차원 이상의 큐브도 시각적으로 표현이 가능하다. (이산적인 0, 1만 값으로 가지면 되서 가능)
• 큐브에 truth table mapping하는 법
  
  • 솔직히 mapping은 그냥 하면 된다. 이제 minimize시키는 방법?
  • 사실 minimize한다는 것은 Uniting theorem을 통해서 없애는 것의 연속이다.
  • 어떻게 해야 Uniting theorem을 잘 사용할 수 있을까? 에 대한 해답이 바로 Boolean Cube이다. (Uniting theorem을 사용해야 할 대상을 더 잘 시각화 해줌)
  • Boolean Cube에서 이웃(adjacent)한 색칠된 점은 Uniting theorem을 통해서 축약될 수 있다.
  • directly adjacent한 on-set의 원소들의 group은 adjacency plane이라고 부른다.
  • adjacency plane 단위로 계속 쪼갤 수 있는데, 3차원 cube의 경우 2차원 plane 전체가 on-set일 수도 있는데, 이 경우에는 변수 1개로 축약되게 된다.
  • generalization : n-dimensional cube에서 m-dimensional adjacency plane이 있다면 n - m literal의 term으로 축약된다.
  • truth table의 1을 포함하는 평면의 개수가 많을수록 항의 개수가 많아진다.

Karnaugh Maps

• 얘는 그냥 책 보셈.
• Karnaugh Maps랑 위에 나와있는 Boolean Cubes랑 어떤 식으로 대응이 되는지 머리속으로 그림 그려보면 될 듯. Karnaugh map의 한 칸이 Boolean cube의 한 꼭짓점에 대응이 된다.

Multilevel Logic

• 아까까지 했던 방식은 two-level을 가진 minimum한 상태를 만들기 위한 방식이었다.
• two-level로 한정하지 않는다면??
  • ex)
    
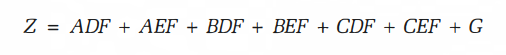
    • 이 경우, two-level 관점에서는 minimum SOP에 해당한다.
    • 만약 이와 별개로 더 factoring을 진행한다면?
      
      위와 같은 결과가 나오고, gate 수가 확 줄게 된다. 하지만 level은 3으로 늘어나게 됨.
    • pros & cons
      • 당연히 level이 한 단계 높아지니까 더 오래 걸리겠지.
      • 하지만 minimum SOP의 경우 하나의 gate에 들어오는 input이 굉장히 많았기 때문에 여기서 delay가 더 발생하게 된다.
      • 일단 gate의 수와 literal의 수가 음청 줄어들음.
• 요약
  • two-level과 multilevel의 속도 차이는 확실하게 누가 좋다 안 좋다 말할 수가 없다.
  • multilevel의 경우 gate가 더 적은 인자를 받게 되어(factor의 기능) 속도가 빨라진다.
  • 하지만 level 자체가 증가하므로 delay가 더 발생한다.
• 3-input : 2-input에 비해 적어도 2배이상 느림
• 4-input : 3-input에 비해 적어도 2배이상 느림

Motivation for Multilevel Minimization

여기는 책 읽어보셈.