문제 해결 패턴

문제 해결 패턴

빈도수 세기 패턴

same([1, 2, 3], [4, 1, 9]); // true;
same([1, 2, 3], [1, 9]); // false;
same([1, 2, 3], [4, 4, 1]); // false;

// 1) 중첩 loop를 사용
function same(arr1, arr2) {
  if (arr1.length !== arrw.length) {
    return false;
  }
  for (let i = 0; i < arr.length; i++) {
    let correctIndex = arr2.indexOf(arr[i] ** 2);
    if (correctIndex === -1) {
      return false;
    }
    arr2.splice(correctIndex, 1);
  }
  return true;
}

• 시간복잡도 -> O(n^2)

// 2) frequency counters 사용
function same(arr1, arr2) {
  if (arr1.length !== arr2.length) {
    return false;
  }
  let frequencyCounter1 = getCounter(arr1);
  let frequencyCounter2 = getCounter(arr2);

  for (let key in frequencyCounter1) {
    if (!(key ** 2 in frequencyCounter2)) {
      return false;
    }
    if (frequencyCounter2[key ** 2] !== frequencyCounter1[key]) {
      return false;
    }
  }
  return true;
}

const getCounter = (arr) => {
  let frequencyCounter = {};
  for (let val of arr) {
    frequencyCounter[val] = (frequencyCounter[val] || 0) + 1;
  }
  return frequencyCounter;
};

• 시간복잡도 -> O(n)

🌿 애너그램 과제

function validAnagram(first, second) {
  if (first.length !== second.length) {
    return false;
  }

  const lookup = {};

  for (let i = 0; i < first.length; i++) {
    let letter = first[i];
    // if letter exists, increment, otherwise set to 1
    lookup[letter] ? lookup[letter] += 1 : lookup[letter] = 1;
  }
  console.log(lookup)

  for (let i = 0; i < second.length; i++) {
    let letter = second[i];
    // can't find letter or letter is zero then it's not an anagram
    if (!lookup[letter]) {
      return false;
    } else {
      lookup[letter] -= 1;
    }
  }

  return true;
}

// {a: 0, n: 0, g: 0, r: 0, m: 0,s:1}
validAnagram('anagrams', 'nagaramm')

⭐️ 다중 포인터 패턴

이 패턴의 개념은 인덱스나 위치에 해당하는 포인터나 값을 만든 다음

특정 조건에 따라 처음 or 끝 or 중간 지점을 향해 이동시키는 것이다.

배열이나 문자열과 같은 일종의 선형 구조, 이중 연결리스트, 단일 연결 리스트를 만들 수 있다.

쉽게 한 쌍의 값이나 조검을 충족시키는 무언가를 찾는다고 생각하면된다.

다중 포인터 패턴을 할 수 있는 조건

정렬된 배열이어야 함 (오름차순)

정렬된 배열(오름차순)을 인자로 받는 sumZero함수를 만든다.
이 함수는 한 숫자를 가져와 다른 숫자에 더하면 0이 되는 쌍을 찾는다.
더하면 0이 되는 쌍이 없다면 undefined를 반환한다.

• 예시
  sumZero([-3,-2,-1,0,1,2,3]) // [-3,3]
  sumZero([-2,0,1,3]) // undefined
  sumZero([1,2,3]) // undefined

sumZero([-3, -2, -1, 0, 1, 2, 3]); // [-3, 3]
sumZero([-2, 0, 1, 3]); // undefined
sumZero([1, 2, 3]); // undefined

// 1) 중첩 loop를 사용
function sumZero(arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = i + 1; j < arr.length; j++) {
      if (arr[i] + arr[j] === 0) {
        return [arr[i], arr[j]];
      }
    }
  }
}

• 시간복잡도 -> O(n^2)

// 2) 다중 포인터 패턴 사용
function sumZero(arr) {
  let left = 0;
  let right = arr.length - 1;
  while (left < right) {
    let sum = arr[left] + arr[right];
    if (sum === 0) {
      return [arr[left], arr[right]];
    } else if (sum > 0) {
      right--;
    } else {
      left++;
    }
  }
}

• 시간복잡도 -> O(n)

💋 고유값 세기 솔루션

Implement a function called countUniqueValues, which accepts a sorted array, and counts the unique values in the array. There can be negative numbers in the array, but it will always be sorted.
정렬이 되어있는 배열에서 고유의 값들의 갯수를 세는 함수를 실행하라. 배열에는 음수가 있을 수 있으나 항상 정렬이 되어있다.
Examples:
countUniqueValues([1,1,1,1,1,2]) // 2
countUniqueValues([1,2,3,4,4,4,7,7,12,12,13]) // 7
countUniqueValues([]) // 0
countUniqueValues([-2,-1,-1,0,1]) // 4
Note:
Time Complexity - O(n)
Space Complexity - O(n)

function countUniqueValues(arr){
    if(arr.length === 0) return 0;
    var i = 0;
    for(var j = 1; j < arr.length; j++){
     // console.log(arr[i],arr[j])
        if(arr[i] !== arr[j]){
            i++;
            arr[i] = arr[j]
          console.log(arr[i],i)
        }
    }
    return i + 1;
}
countUniqueValues([1,2,2,5,7,7,99]) //1,2,5,7,99

i
[1,1,2,3,3,4,5,6,6,7]
  j -> move right
만약 i와 j가 다르다면 i의 index에 j를 넣고
i+1위치에서 다시 검사
  i
[1,2,2,3,3,4,5,6,6,7]
    j -> move right
    i
[1,2,3,3,3,4,5,6,6,7]
      j -> move right
...loop
반복문이 끝날때는 아래와 같이 된다.
            i
[1,2,3,4,5,6,7,6,6,7]
                  j
i index의 위치까지 중복되지 않는 배열이기 때문에
고유한 값의 갯수는 i + 1이다.

경계조건 : 빈배열을 받았을 때 1을 return하게 되므로, 0을 return 하도록 예외처리한다.

기준점 간 이동 배열 패턴 (sliding window)

배열이나 문자열과 같은 일련의 데이터를 입력하거나 특정 방식으로 연속적인 해당 데이터의 하위 집합을 찾는 경우에 유용

ex) maxSubarraySum
붙어있는 배열중에 가장 큰 합 찾기

maxSubarraySum([1, 2, 5, 2, 8, 1, 5], 2); // 10
maxSubarraySum([1, 2, 5, 2, 8, 1, 5], 4); // 17
maxSubarraySum([4, 2, 1, 6], 1); // 6
maxSubarraySum([4, 2, 1, 6, 2], 4); // 13
maxSubarraySum([], 4); // null

// 1) 중첩 loop를 사용
function maxSubarraySum1(arr, num) {
  if (num > arr.length) {
    return null;
  }
  // 배열이 모두 음수라면 가장 큰 합이 음수이기 결과의 초기값은 가장 작은 음수
  let max = -Infinity;
  // loop문이 i부터 연속된 num만큼의 요소를 더하기 때문에 loop는 배열의 마지막 인덱스 - num
  for (let i = 0; i < arr.length - num + 1; i++) {
    temp = 0;
    for (let j = 0; j < num; j++) {
      temp += arr[i + j];
    }
    if (temp > max) {
      max = temp;
    }
  }
  return max;
}
showReturn(maxSubarraySum1([2, 6, 9, 2, 1, 8, 5, 6, 3], 3));

• 시간복잡도 -> O(n^2)

// 2) 기준점 간 이동 배열 패턴
function maxSubarraySum(arr, num) {
  let maxSum = 0;
  let tempSum = 0;
  if (num > arr.length) return null;
  for (let i = 0; i < num; i++) {
    maxSum += arr[i];
  }
  tempSum = maxSum;
  for (let i = num; i < arr.length; i++) {
    tempSum = tempSum - arr[i - num] + arr[i];

    maxSum = Math.max(maxSum, tempSum);
  }
  return maxSum;
}

• 시간복잡도 -> O(n)

분할과 정복 패턴 (divide and conquer)

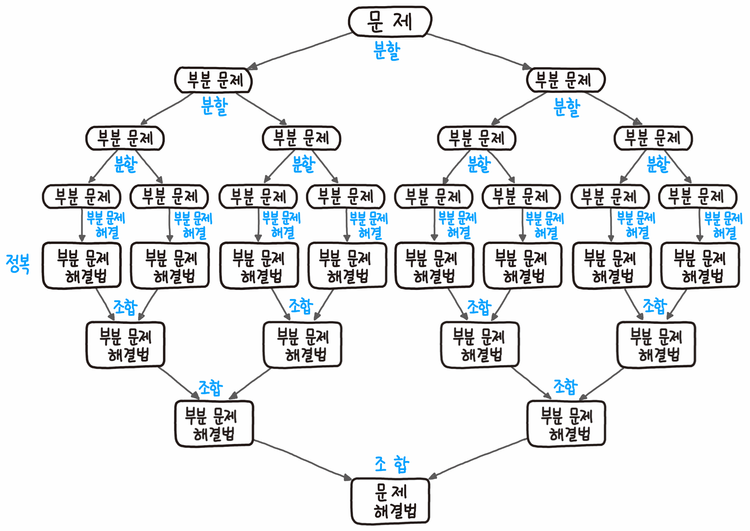
배열을 세분해서 탐색(i.e search)

// Linear Search
function search(arr, val) {
  for (let i = 0; i < arr.length; i++) {
    if (arr[i] === val) {
      return i;
    }
  }
  return -1;
}

• 시간복잡도 -> O(n)

// Binary Search
function search(arr, val) {
  let min = 0;
  let max = array.length - 1;

  while (min <= max) {
    let middle = Math.floor((min + max) / 2);
    let curentElement = array[middle];
    if (array[middle] < val) {
      min = middle + 1;
    } else if (array[middle] > val) {
      max = middle - 1;
    } else {
      return middle;
    }
  }
  return -1;
}

• 시간복잡도 -> Log(n)