6장: 관계 데이터 연산

관계 데이터 연산의 개념

1. 관계 대수:low-lovel language(Assembly어)에 해당하며, 데이터의 처리 과정을 순서대로 기술한 것

2. 관계 해석:high-level language(python)에 해당, 처리를 원하는 데이터가 무엇인지만 기술, SQL문이 주로 해당된다

• 관계 대수:절차 언어라고 하며, 폐쇄 특성이 있음

  폐쇄 특성:피연산자도 릴레이션, 연산의 결과도 릴레이션인 특성

관계 대수의 연산자

1. 일반 집합 연산자:릴레이션이 투플의 집합이라는 개념을 이용
2. 순수 관계 연산자

일반 집합 연산자의 특성

• 합집합,교집합,차집합은 피연산자인 두 릴레이션이 합병 가능해야 함

  • 합병 가능 조건
  1. 두 릴레이션의 차수(속성의 수)가 같아야 함
  2. 서로 대응되는 속성의 도메인(값의 범위, 자료형)이 같아야 함

• 합집합:R∪S로 표기한다

  • 차수: 릴레이션 R과 S의 차수와 같음
  • 카디널리티<=R+S(∵튜플은 중복x)
  • 교환법칙 성립:R∪S=S∪R, 결합법칙 성립:(R∪S)T=R∪(S∪T) -> 튜플의 무순서

• 교집합:R∩S로 표기한다
  - 차수:릴레이션 R과 S의 차수와 같음

  • 카디널리티: 최솟값은 0, 최댓값은 min(R,S)
  • 교환법칙 성립:R∩S=S∩R, 결합법칙 성립:(R∩S)∩TR∩(S∩T)

• 차집합:R-S로 표기한다
  - 차수:릴레이션 R과 S의 차수와 같음

  • R-S의 카디널리티:최솟값은 0(R=S일 경우), 최댓값은 R
  • S-R의 카디널리티:최솟값은 0, 최댓값은 S
    📢교환법칙과 결합법칙 모두 성립하지 않음

• 카티션 프로덕트:RxS로 표기한다, R에 속한 각 투플과 S에 속한 각 투플을 모두 연결하여 만들어진 새로운 투플로 결과 릴레이션을 구성
  - 차수:R의 차수+S의 차수

  • 카디널리티:R카디널리티(행)XS카디널리티(행)
  • 교환법칙 성립:RXS=SXR, 결합법칙 성립:(RXS)XT=RX(SXT) <- 속성의 무순서

순수 관계 연산자

• 셀렉트(select):릴레이션에서 조건을 만족하는 투플만 선택하여 결과 릴레이션을 구성, ∂_조건식(릴레이션)으로 표기한다
  - 수평적 부분집합

  • 조건식:비교 연산자(>,>=,<,<=,=,≠)와 논리 연산자(∧,∨,￢:순서대로 and,or,not)를 이용해 작성
  • 폐쇄 특성에 의해 교환법칙 성립

• 프로젝트(project):릴레이션에서 선택한 속성의 값으로 결과 릴레이션을 구성,π_속성리스트(릴레이션)으로 표기한다
  - 수직적 부분집합
  📢 결과 릴레이션에서 동일한 투플은 중복되지 않고 한 번만 나타남

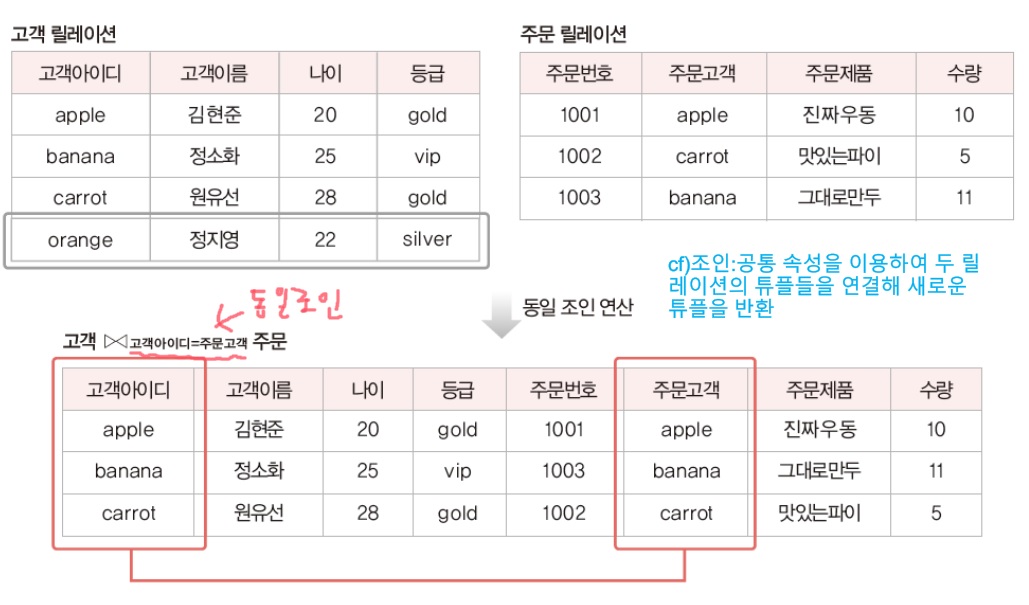
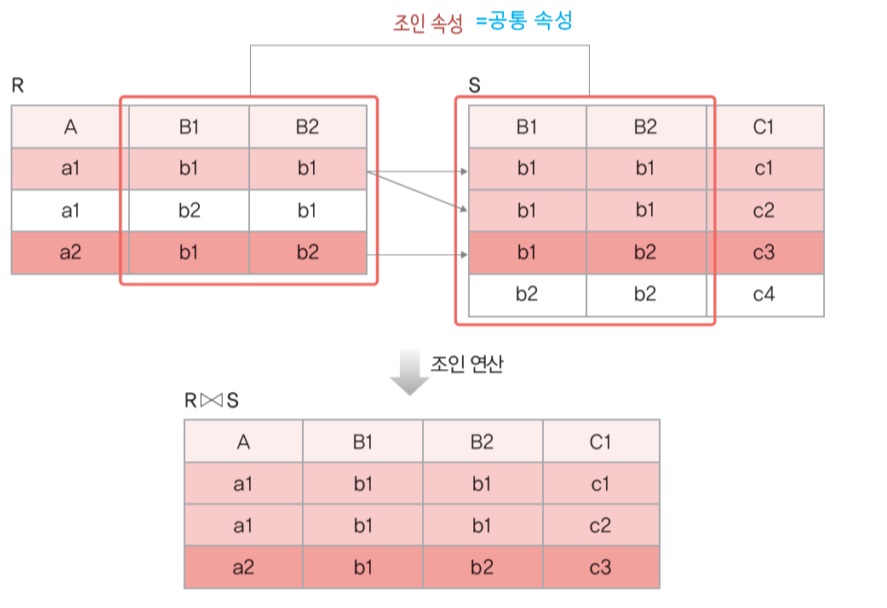
• 세타 조인: 공통 속성을 이용하여 두 릴레이션의 투플들을 연결해 새로운 투플을 반환, Rꗯ_AθB S로 표기(θ는 비교연산자를 의미)
  - 결과 릴레이션의 차수:R의 차수+S의 차수

  • 동일조인: θ연산자가 "="인 세타 조인

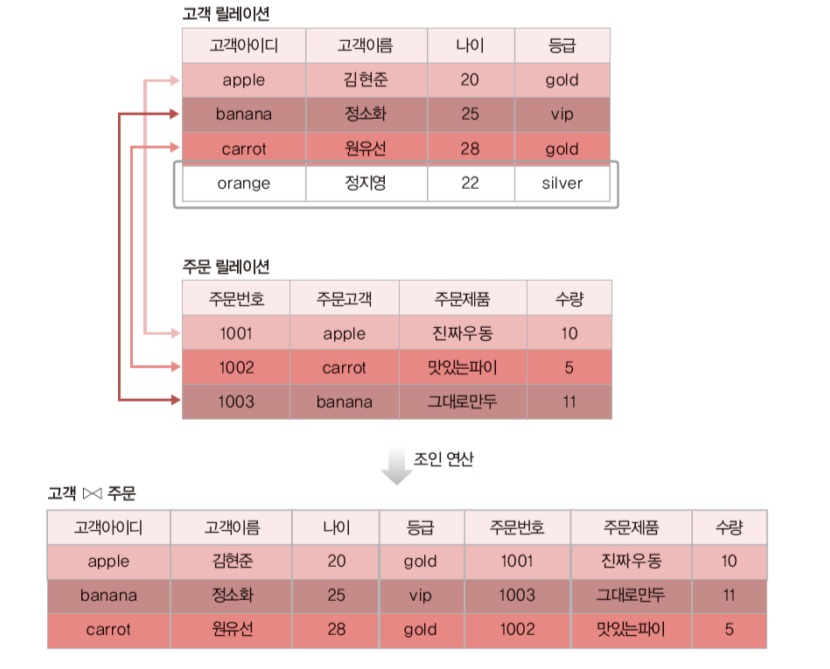
• 조인 또는 자연조인:동일조인에서 중복 투플을 제거한 결과 릴레이션

대소관계: 조인(또는 자연조인) ⊂ 동일조인 ⊂ 세타조인
1. 세타조인: 주어진 조인 조건을 만족하는 카티션 프로덕트
2. 동일조인: 조인 연산자가 equal
3. 조인(또는 자연조인): 동일조인에서 중복 투플을 제거한 릴레이션

• 동일조인과 자연조인의 결과 비교

1. 동일조인
   

2. 자연조인
   (1)
   

(2)

• 디비전(division):R÷S로 표기하며, R이 S의 모든 속성을 포함하고 있어야 연산이 가능함(도메인이 같아야 한다는 의미)
  
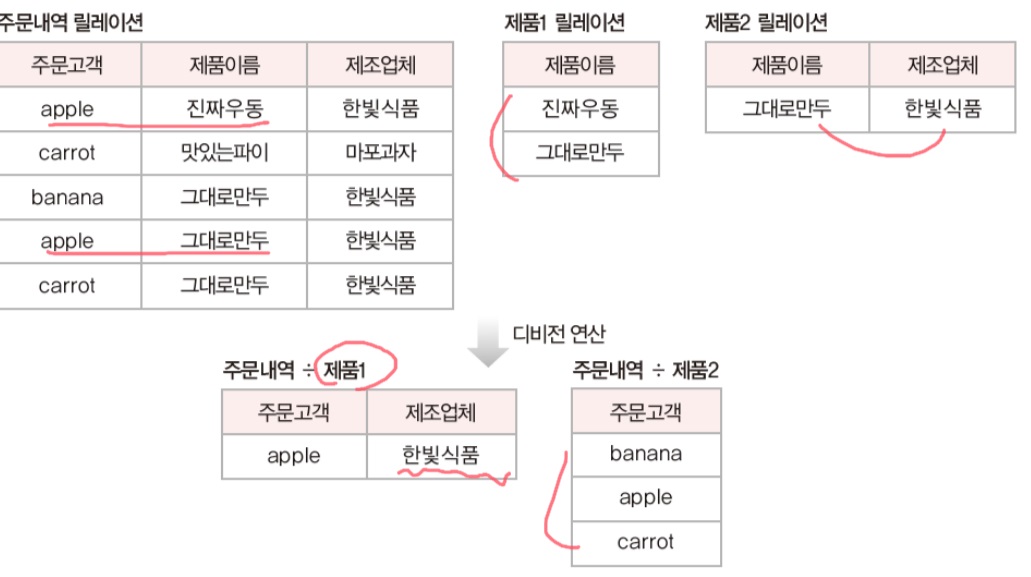
  📢디비전은 해당 릴레이션의 속성의 값을 모두 만족해야함

확장된 관계 대수 연산자

• 세미 조인:R∝S=RꗯN(π_z(S))로 표기, S를 조인 속성으로 프로젝트 연산한 후, R에 자연 조인(동일조인+중복 투플제거)하여 결과 릴레이션을 구성
  ->프로젝트로 공통 속성의 값을 먼저 추출한 후, S에 참가하는 R의 투플을 조인

• 장점:최종 조인에 필요한 데이터만 전송할 수 있어, 조인 연산비용을 크게 줄일 수 있음

• 교환법칙 불성립:S에 참가하는 R의 투플과, R에 참가하는 S의 투플이 서로 다르기 때문

• Rꗯ_N S=(R∝S)ꗯ_N S=(S∝R)ꗯ_N R

• 자연 조인과 세미 조인의 비교
  (1)자연 조인 연산
  

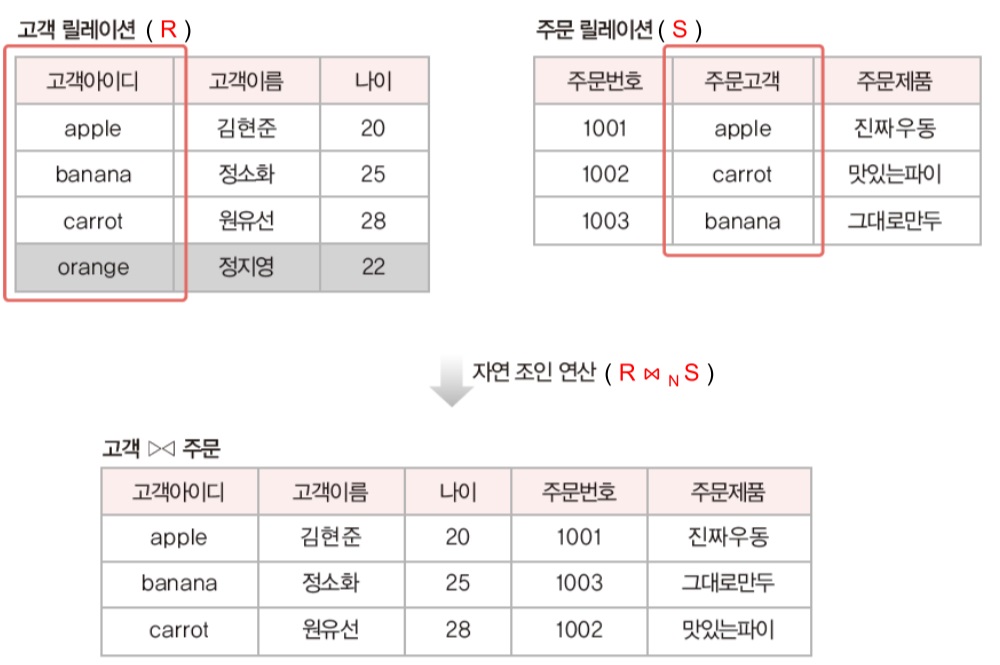
(2)세미 조인 연산

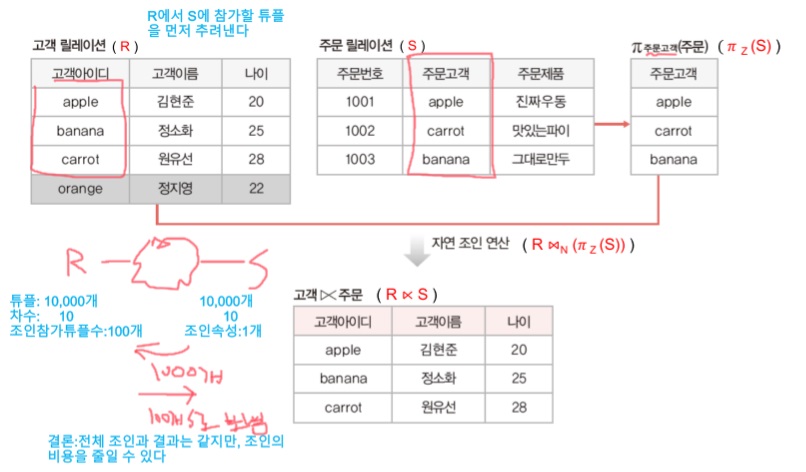
• 외부 조인:자연 조인 연산에서 제외되는 투플도 결과 릴레이션에 포함시키는 조인,
  R ꗯ+ S로 표기한다