ML 지도학습

회귀

• 모델: LinearRegression, Ridge, Lasso.. 등

• 평가 Metric: $R^2$

  $R^2=1-\frac{\sum_{i=1}^{n}(오차)^2}{\sum_{i=1}^{n}(편차)^2}$

  $=1-\frac{\sum_{i=1}^{n}(실제값-예측값)^2}{\sum_{i=1}^{n}(실제값-실제평균)^2}$

  $=1-\frac{\sum_{i=1}^{n}(y_i-\widehat{y_i})^2}{\sum_{i=1}^{n}(y_i-\bar{y_i})^2}$

• cost function: MSE(Mean Squared Error)

  $MSE=\frac{1}{n}\sum_{i=1}^{n}(y_i-\widehat{y_i})^2$

  $=\frac{1}{n}\sum_{i=1}^{n}(y_i-(w_1\cdot{x}+(1\cdot{w_0})))^2$

분류

• 모델: LogisticRegression, SGDClassifier.. 등
• 평가 Metric: Accuracy, Preicision, Recall, F1_score

  
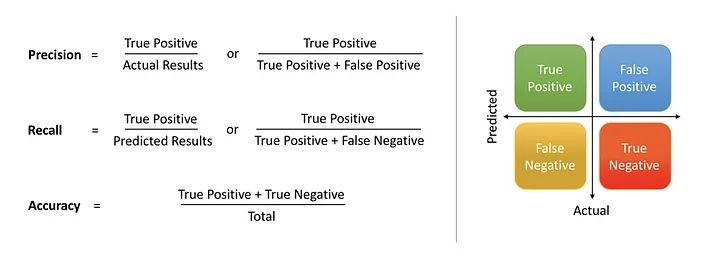
  https://medium.com/@shrutisaxena0617/precision-vs-recall-386cf9f89488

  $Accuracy = \frac{True Positive + True Negative}{Total}$

  $Precision = \frac{True Positive}{True Positive + False Positive}$

  $Recall = \frac{True Positive}{True Positive+False Negative}$

  $F1-Score=2*\frac{recall * precision}{recall+precision}$

• cost function: log_loss, hinge

  $loss=plog_e(\widehat{p})$

  $=plog_e(\frac{1}{1+e^{-z}})$

  $=plog_e(\frac{1}{1+e^{(w_1\cdot{x}+(1\cdot{w_0}))}})$

• hinge

  • 0보다 작은 값에 대해서는 그대로 출력, 0과 같거나 0보다 큰 값에 대해서는 0으로 처리하는 function입니다.
  • $loss = max\{0, 1 - (\widehat{y}\cdot{y})\}$
    
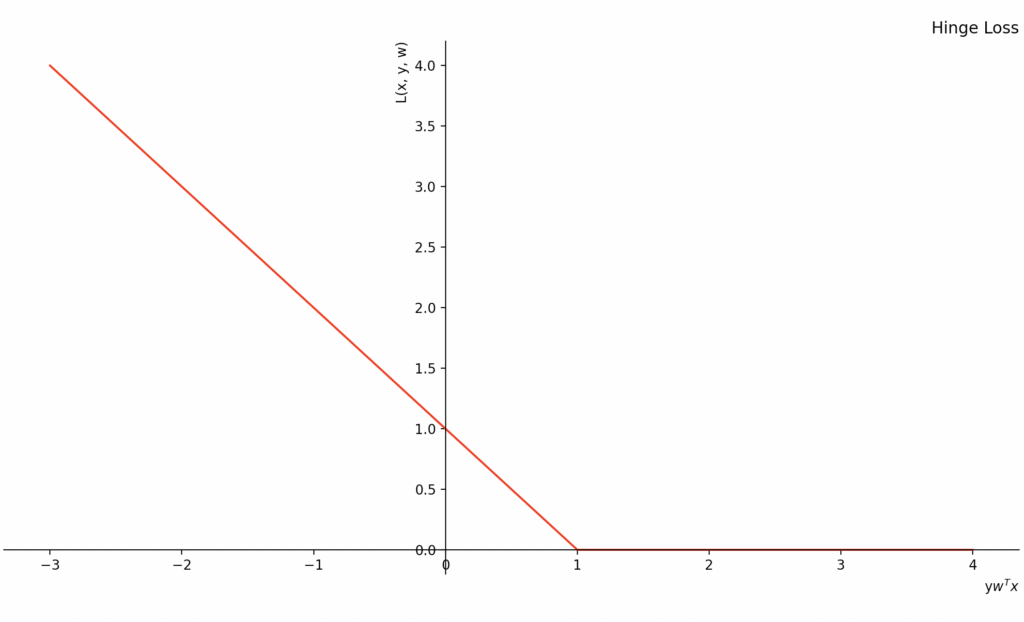
    https://www.baeldung.com/cs/hinge-loss-vs-logistic-loss