
🐢 알고리즘 강의
유튜브
바킹독의 실전 알고리즘강의를 듣고 내용을 정리합니다.
🍀 시간복잡도
입력의 크기와 문제를 해결하는데 걸리는 시간의 상관관계
✔️ 빅오표기법(Big-O Notation)
주어진 식을 값이 가장 큰 대표항만 남겨서 나타내는 방법
ex)
- 5N+3, 2N+10lgN ... 👉
O(N) - 6N²+2N+4 👉
O(N²) - NlgN+30N+10 👉
O(NlgN) - 5, 16, 36 ... 👉
O(1)
✔️ lgN(=logN) 배경지식
lgN: 해당 수가 2의 몇 거듭제곱인지를 의미
ex) lg2=1, lg4=2, lg8=3 ...
절반으로 계속 쪼개지는 상황일 때의 시간 복잡도는 lgN이다.
ex) 사람이 16명이면 4번, 32명이면 5번, 64명이면 6번... 의 연산을 수행해야 한다.
✔️ 대표적인 시간복잡도
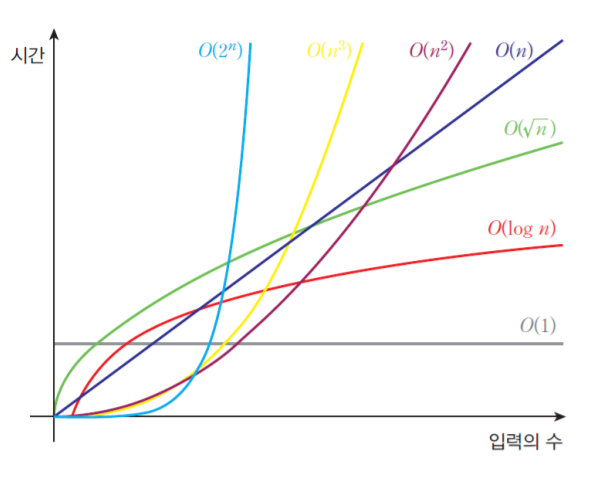
O(1) < O(lgN) < O(N) < O(NlgN) < O(N²) < O(2^n) < O(N!)
-
O(lg N): 로그 시간 -
O(N): 선형 시간 -
O(lg N)부터 O(N²)까지: 다항시간
lg N 혹은 N의 거듭제곱끼리의 곱으로 시간복잡도가 나타내어지면 이를 다항 시간이라고 함. -
O(2^N): 지수 시간
O(2N)이 필요한 풀이는 대부분 시간 제한을 통과하기 힘들다. -
O(N!): 팩토리얼은 지수 시간보다 훨씬 더 가파르게 올라간다. 당장 12!만 해도 거의 5억이라 O(N!)이 필요한 알고리즘도 대부분 시간 제한을 통과하기 힘들다.
✔️ N의 크기에 따른 허용 시간복잡도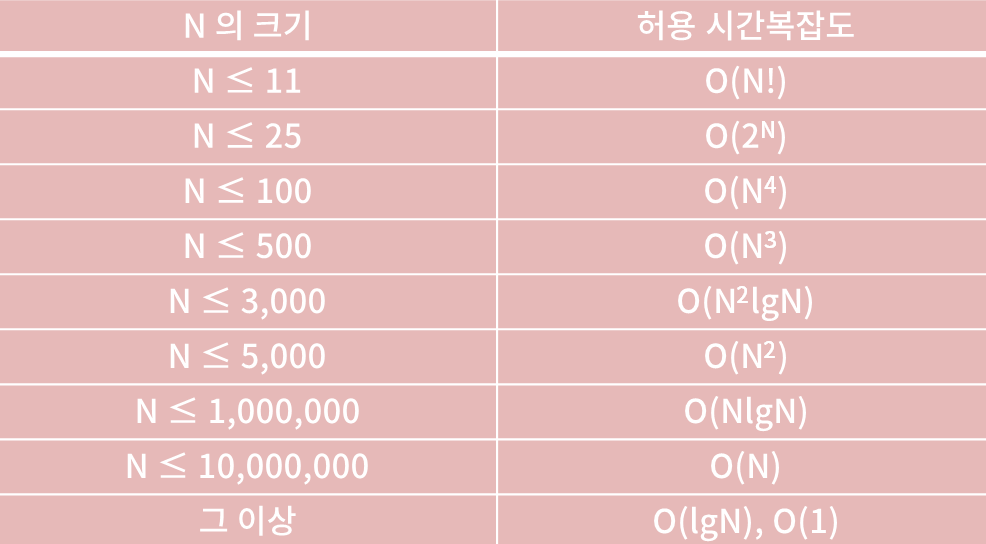
- 이 기준이 절대적인 것은 아님. 대략적인 느낌만 잡기
✔️ 문제를 풀 때 해야할 일
주어진 문제를 보고 풀이를 떠올린 후에 무턱대고 바로 그걸 짜는게 아니라 내 풀이가 이 문제를 제한 시간 내로 통과할 수 있는지, 즉 내 알고리즘의 시간복잡도가 올바른지를 꼭 생각해봐야 함.
🍀 공간복잡도
입력의 크기와 문제를 해결하는데 필요한 공간의 상관관계를 의미
예를 들어 크기 N짜리 2차원 배열이 필요하면 O(N²)이고, 따로 배열이 필요 없으면 O(1)
그런데 코딩테스트에서 대부분의 경우 공간복잡도의 문제보다는 시간복잡도 때문에 문제를 많이 틀리게 된다. 그래서 공간복잡도는 크게 신경을 안써도 된다.
대신 문제를 풀 때, 메모리 제한이 512MB일 때 int 변수를 대략 1.2억개 정도 선언할 수 있다는 것을 기억해두기. 이건 int 1개가 4바이트라는 것을 이용해 계산할 수 있다.
만약 떠올린 풀이가 크기가 5억인 배열을 필요로 할 때 해당 풀이는 주어진 메모리 제한을 만족하지 못하므로 틀린 풀이라는 것을 빠르게 깨닫고 다른 풀이를 고민할 수 있다.
🍀 정수 자료형
✔️ 정수 자료형 종류
-
char: 1 byte = 8 bit

-
short: 2 byte = 16 bit

-
int: 4 byte = 32 bit

-
long long: 8byte = 64 bit

short는 딱히 쓸 일이 없고, 정수를 표현할 때 주로 int나 long long을 쓴다.
int가 long long보다 연산 속도와 메모리 모두 우수하지만 80번째 피보나치 수를 구하는 문제와 같이 int 자료형이 표현할 수 있는 범위를 넘어서는 수를 저장해야 하면 반드시 long long 자료형을 사용해야 한다.
✔️ Integer Overflow
자료형의 범위를 벗어났을 때 결과가 옳지 않게 나오는 것
앞으로 머리로는 Integer Overflow를 익혔지만 분명 실제로 문제를 풀 때 이 실수를 여러 번 저지르게 될 것이다. 그래도 이 실수로 시간을 엄청 버리고 나면 그 다음엔 실수를 덜하게 될 것!
만약 문제에서 unsigned long long 범위를 넘어서는 수를 저장할 것을 요구한다면 string을 활용해서 저장해야 한다. 그리고 그 수로 연산을 해야 하는 문제는 코딩테스트에 안나오는게 정상이긴 한데, 만에 하나 나왔다 치면 그냥 Python을 쓰는게 C++로 꾸역꾸역 구현하는 것 보다 훨씬 편하다.
🍀 실수 자료형
✔️ 실수 자료형 종류
-
float: 4 byte = 32 bit -
double: 8 byte = 64 bit

sign field: 해당 수가 음수인지 양수인지 저장하는 필드exponent field: 과학적 표기법에서의 지수를 저장하는 필드fraction field: 유효숫자 부분을 저장하는 필드
- 각 필드의 크기가
float은 1, 8, 23 bit이고double은 1, 11, 52 bit
예시
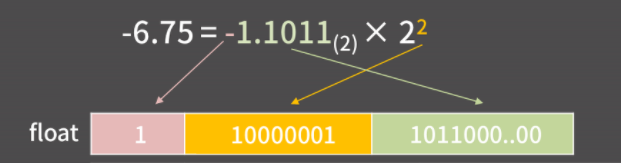
-
sign field(음수/양수 저장 필드) : -6.75의 부호가 음수여서 1 기록 -
exponent field(지수 저장 필드) : 지수는 2인데, 여기에 127을 더한 129를 2진수로 변환한 10000001 기록
cf) 127을 더하는 이유 : 이렇게 해줘야 음수 지수승도 exponent field 안에 잘 넣을 수 있다. -
fraction field(유효숫자 저장 필드) : 1.1011에서 맨 앞의 1은 뺀 1011을 기록. 소수점 부터 2^(-1), 2^(-2)자리이기 때문.
이렇게 실수를 저장하는 방식을 IEEE-754 format이라고 한다.
✔️ 실수의 성질
- 실수의 저장/ 연산 과정에서 반드시 오차가 발생할 수 밖에 없다.
아주 대표적인 예가 0.1+0.1+0.1이 0.3과 다르다고 하는 경우이다.
이러한 경우가 발생하는 이유는 유효숫자가 들어가는 fraction field가 유한하기 때문에 2진수 기준으로 무한소수인걸 저장하려고 할 때에는 어쩔 수 없이 float은 앞 23 bit, double은 앞 52 bit까지만 잘라서 저장할 수 밖에 없다.
0.1은 이진수로 나타내면 무한소수여서 애초에 오차가 있는 채로 저장이 됐고 그걸 3번 더하다보니 오차가 더 커져서 0.3과 다르다고 나온 것이다.
그렇다면 fraction field를 가지고 각 자료형이 어디까지 정확하게 표현할 수 있을까?
-
float: 유효숫자가 6자리. 상대 오차 10^(-6)까지 안전 -
double: 유효숫자가 15자리. 상대 오차 10^(-15)까지 안전 -
'상대 오차가 10-15까지 안전하다'는 말의 의미 : 원래 참값이 1이라고 할 때, 1-10-15 에서 1+10-15 사이의 값을 가진다는게 보장된다는 의미.
이를 통해 오차가 생기는 것 자체는 막을 수가 없지만 오차가 어느 정도인지는 알 수 있다.
기억해할 점
상대 오차의 허용 범위에서 볼 수 있듯 float, double두 자료형끼리 차이가 굉장히 크기 때문에 실수 자료형이 필요하면 꼭 float 대신 double을 써야한다.
실수 자료형은 필연적으로 오차가 있으니까 실수 자료형이 필요한 문제면 보통 문제에서 절대/상대 오차를 허용한다는 단서를 준다. 그런데 만약 이런 표현이 없다면 열에 아홉은 실수를 안쓰고 모든 연산을 정수에서 해결할 수 있는 문제일 것!
double에long long범위의 정수를 함부로 담으면 안된다.
double은 유효숫자가 15자리인데 long long은 최대 19자리이기 때문에 double에 long long 범위의 정수를 담을 경우 오차가 섞인 값이 저장될 수 있다.
다만, int는 최대 21억이기 때문에 double에 담아도 오차가 생기지 않는다.
- 실수를 비교할 때는 등호를 사용하면 안된다.
오차 때문에 두 실수가 같은지 알고 싶을 때에는 둘의 차이가 아주 작은 값, 대략 10(-12) 이하면 동일하다고 처리를 하는게 안전합니다.
cf) 10^(-12) = 1e-12
