오늘 자료구조 수업에서 배운 내용인 빅오표법과 시간 복잡도간의 관계에 대해 살펴보도록 하겠다. (나의 첫번째 velog ㅎㅎ 😆😆 부족한점 있으면 나중에 보충 해야지)
📌 -빅오표기법 :연산의 횟수를 대략적으로 표기한것
ex) n=1000인경우
T(n)=n제곱+n+1
두개의 함수f(n)과 g(n)이 주어졌을 때, 모든 n>=n₀에 대하여 |f(n)|<=c|g(n)
을 만족하는 2개의 상수 c와 n₀가 존재하면 f(n)=O(g(n))이다.
-빅오는 함수의 상한을 표기한다.
ex) n>= 5이면 2n+1<10n 이므로 2n+1=O(n)
📌 <빅오 표기법의 종류>
-O(1) :상수형
-O(log n): 로그형
-O(nlog n): 선형 로그형
------------------------> 2차형 이상의 빅오 표기법은 좋지 않은 알고리즘
-O(n제곱): 2차형
-O(n세제곱) :3차형
-O(2의 n 제곱) : 지수형
-O(n!):펙토리얼형
<복잡도의 종류>
-(시간 복잡도)(Time Complexity)
-O(1) :상수형
-O(log n): 로그형
-O(nlog n): 선형 로그형
-O(n제곱): 2차형
-(공간 복잡도) (space Complexity)
-O(1) :상수형
-O(log n): 로그형
-O(nlog n): 선형 로그형
-O(n제곱): 2차형
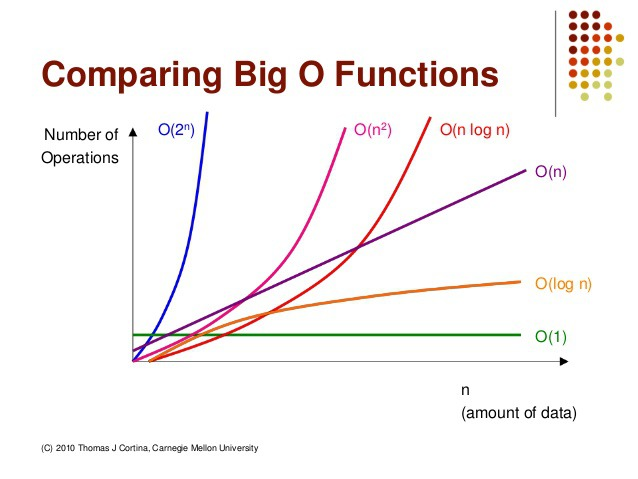 <그림1>
<그림1>
🔑===> <그림1>참고, 시간 복잡도를 떨어뜨리게 되면 공간을 많이쓰게 됨. 즉, 메모리를 많이쓰면 알고리즘의 성능이 빨라짐.만약 공간 복잡도가 고효율적이라면 알고리즘의 성능이 복잡해지고 느려짐.
📌 <빅오 표기법 외의 표기법>
-빅오메가 표기법
-모든 n>=n₀에 대하여 |f(n)|<=c|g(n)
을 만족하는 2개의 상수 c와 n₀가 존재하면 f(n)=g(n))이다.
-빅오메가는 함수의 하한을 표기한다.
ex) n>=5 이면 2n+1<10n이므로 n=Ω(n)
-빅세타 표기법
-빅세타는 함수의 하한인 동시에 상한을 표시한다.
-f(n)=O(g(n))이면서 f(n) Ω(g(n))이면 f(n)=θ(n)이다.
ex) n>=1이면 n<=2n+1<3n이므로 2n+1=θ(n)이다.
<최선,평균,최악의 경우>
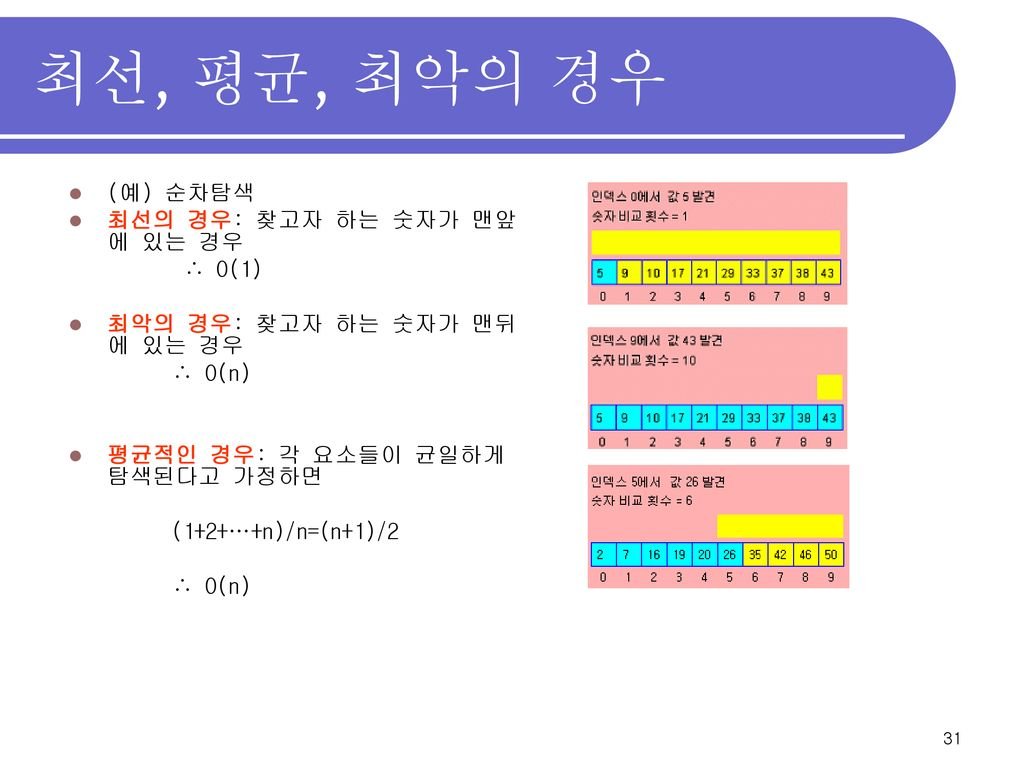
🔑 ===>최악의 경우(worst case): 가장 널리 사용된다. 계산하기 수비고 응용에 따라서 중여한 의미를 가질 수도 있다.
ex) 비행기 관제 업무, 게임, 로보틱스
💡 느낌점:
오늘수업에서 배운 빅오 표기법은 연산의 횟수를 대략적으로 표기한것으로 위에 나와있듯이 빅오 표기법의 개념과 복잡도의 종류에 대해 살펴 봤다. 이를 통해 시간 복잡도를 떨어뜨리게 되면 공간을 많이 쓰게 되어 메모리를 많이 쓰도록 해서 알고리즘의 성능을 빠르게 할 수 있다는 것을 알게 되었다. 또한 반대로 공간 복잡도가 고효율적이라면 알고리즘의 성능이 복잡해지고 느려지는 사실을 그래프와 설명을 통해서 알게 되었다. 나는 이번 수업을 통해 빅오 표기법에 대해 구체적으로 알게 되었고 이제 막 자료구조를 시작하는 학교 수업에서 효율적인 알고리즘이나 코드를 위해 먼저 빅오 표기법이 무엇인지를 가르쳐주는 수업이었다고 생각한다. 그리고 앞으로의 프로그래머로써 알고리즘의 최적화와 효율성을 따져야한다는 생각이 들었다.