Complexity(복잡도)
Complexity : 알고리즘의 성능을 나타내는 척도
컴퓨터는 1초에 대략 3-5억 개 정도의 연산이 가능하다. 다만 AND, OR, 비교, 덧셈과 같은 단순한 연산인지 나눗셈, 곱셈, 대입, 함수 같은 복잡한 연산인 지에 따라 횟수의 차이가 날 수는 있다.
결과를 먼저 말하자면 복잡도가 낮을 수록 좋은 알고리즘이라고 할 수 있다.
Time complexity(시간 복잡도)
Time complexity : 입력의 크기와 문제를 해결하는데 걸리는 시간의 상관 관계
시간 복잡도를 어떻게 구하는 지 알아보기 위해서 간단한 예제를 통해 흐름을 알아볼 수 있다.
# lst -> 리스트 타입
# n -> 정수 타입
def func1(lst, n):
cnt = 0
for i in range(n):
if lst[i] % 5 == 0:
cnt += 1
return cnt위의 코드는 lst[0] 부터 lst[num-1]까지 돌면서 5의 배수일 때 cnt 라는 변수의 값을 1 증가 시킨다.
이 코드는 몇 번의 연산을 수행하는 지 알아보자면
- cnt 변수를 선언하고 0을 넣을 때 : 1
- 반복문이 n번 반복 : n
- 반복문 안에서 lst[i] 값을 5로 나눌 때 : 1
- lst[i] 값을 5로 나눈 나머지가 0인지 판별할 때 : 1
- lst[i]가 5의 배수라면 cnt 값이 증가하므로 : 1
- return cnt = 1
총 1+nx(1+1+1) +1 ⇒ 3n + 2
위의 코드는 3n+2번 연산을 하는데 n의 값에 따라서 연산이 증가한다.
그래서 예시 코드의 연산은 n에 비례한다 라고 말할 수 있고,
시간 복잡도는 입력의 크기와 문제를 해결하는데 걸리는 시간의 상관 관계이기 때문에
예시 코드의 시간 복잡도는 n 이다.
🔽시간 복잡도는 빅오 표기법을 통해 나타내기 때문에 빅오 표기법을 아래에서 알아보자🔽
Big-O Notation(빅오 표기법)
Big-O Notation : 가장 빠르게 증가하는 항만을 고려하는 표기법
| 표기법 | 설명 | 예시 알고리즘 |
|--------------|----------------------|--------------------------|
| O(1) | 상수 시간 복잡도 | 배열에서 요소 하나 찾기 |
| O(logN) | 로그 시간 복잡도 | 이진 검색 |
| O(N) | 선형 시간 복잡도 | 선형 탐색 |
| O(NlogN) | 로그 선형 시간 복잡도 | 퀵 정렬, 병합 정렬 |
| O(N²) | 이차 시간 복잡도 | 버블 정렬, 삽입 정렬 |
| O(N³) | 삼차 시간 복잡도 | 3중 루프 알고리즘 |
| O(2ⁿ) | 지수 시간 복잡도 | 부분집합 생성, 완전탐색 |연산 횟수가 2N³ + 5N² + 1,000,000인 알고리즘이 있다면 시간 복잡도는 O(N³) 라고 부른다
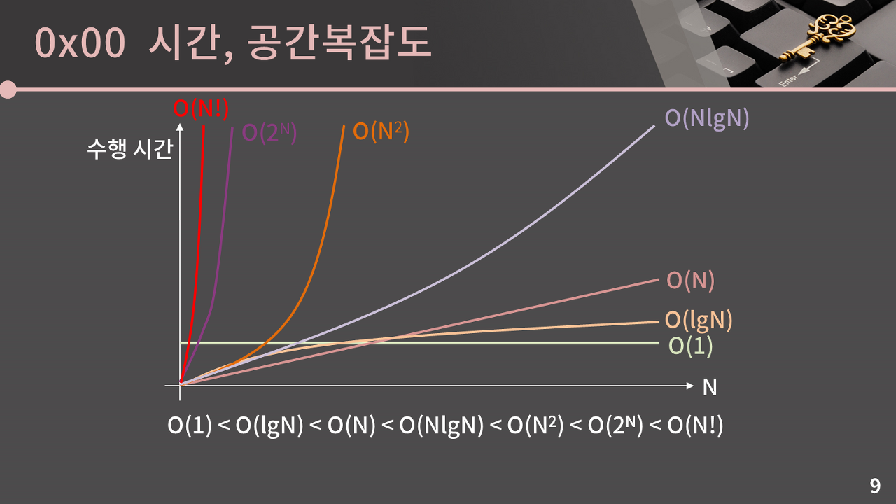
<출처 : https://blog.encrypted.gg/922>
그래프를 보면 N의 크기에 따라 시간 복잡도의 차이가 수행 시간이 큰 영향을 준다는 것을 알 수 있다.
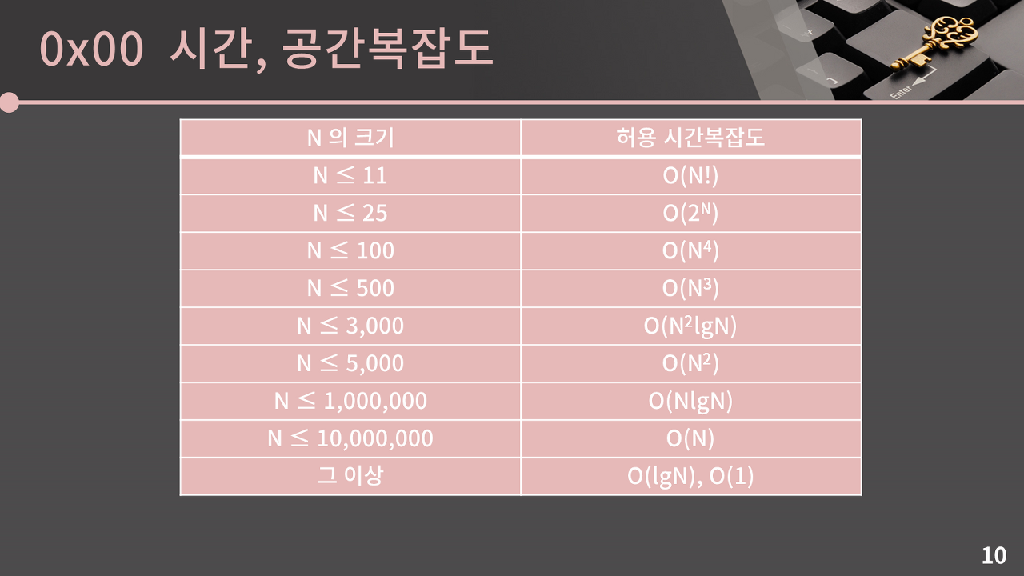
<출처 : https://blog.encrypted.gg/922>
문제에서 주어지는 시간 제한은 대부분 1초에서 5초사이로, 입력의 범위를 보고 요구하는 시간 복잡도가 어느 정도인지를 알 수 있다.
Space complexity(공간 복잡도)
→ 입력의 크기와 문제를 해결하는데 필요한 공간의 상관 관계
→ 알고리즘이 필요로 하는 메모리의 양
빅오 표기법을 사용한 표기법
크기가 N인 1차원 배열이 필요하다면 O(N)
크기가 N인 2차원 배열이 필요하다면 O(N²)
배열이 필요 없다면 O(1)
🍯꿀Tip : 512MB = 1.2억개의 int
