개요
차원 축소는 수 많은 정보 속에서 무엇이 중요한지 알게 해준다.
그런 방법 중 하나가 PCA이다.
PCA?
데이터 분포의 주성분을 찾아주는 방법이다. 주성분은 데이터의 분산이 가장 큰 방향벡터이다.
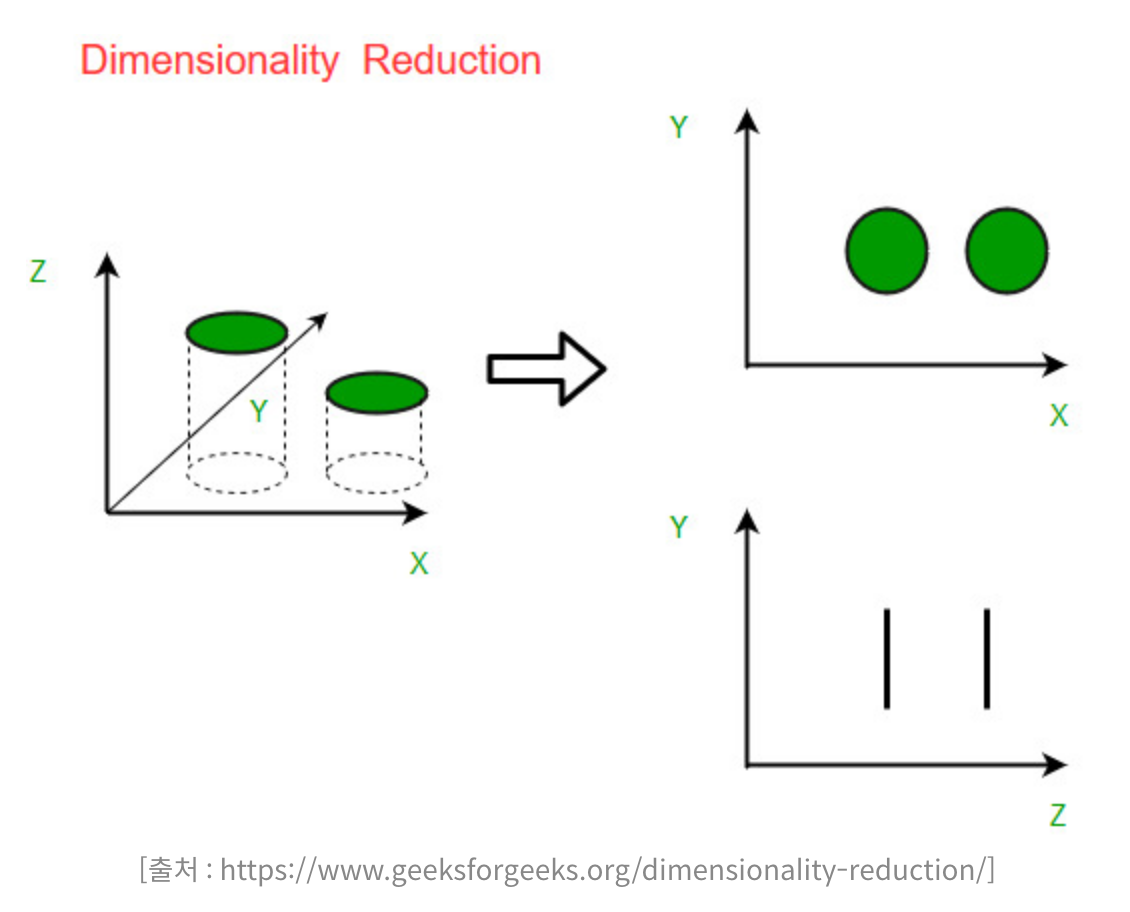
X-Y-Z 좌표축상에 존재하는 데이터를 X-Y,Y-Z 좌표축에 projection했다는 것은 Z, X 좌표축을 무시했다는 뜻이 된다. 그만큼 데이터 손실이 일어난다. 위 그림의 경우 원본 데이터의 특성을 상대적으로 잘 살리면서 차원을 1개 줄인 것은 X-Y이다. 그렇다면 Z축 방향의 정보는 상대적으로 덜 중요하다.(수학적으로는 Z축 방향의 분산이 작다.)고 할 수 있다.
PCA는 효과적인? 방법으로 차원축소를 한다.
T-SNE
기존 차원의 공간에서 가까운 공간에서 가까운 점들은 차원축소된 공간에서도 여전히 가깝게 유지되는 것을 목표로 한다. 예를 들어 784차원의 숫자 이미지를 2차원으로 시각화하여도, 같은 숫자의 이미지끼리 유사한 거리에 놓인다.
PCA는 정보 손실을 최소화하려는 관점을 가지고 있으므로, 그 결과 추출된 PC축은 주성분이라는 물리적 의미를 유지하고 있으며, 공분산을 통해 원본 데이터를 일정 부분 복원할 수 있는 가능성을 가지고 있다. 그러나 T-SNE는 정보 손실량에 주목하지 않으며, 그 결과 저차원 축이 아무런 물리적 의미를 가지지 못합니다. 오직 시각화에만 유리할 뿐이다.
