-
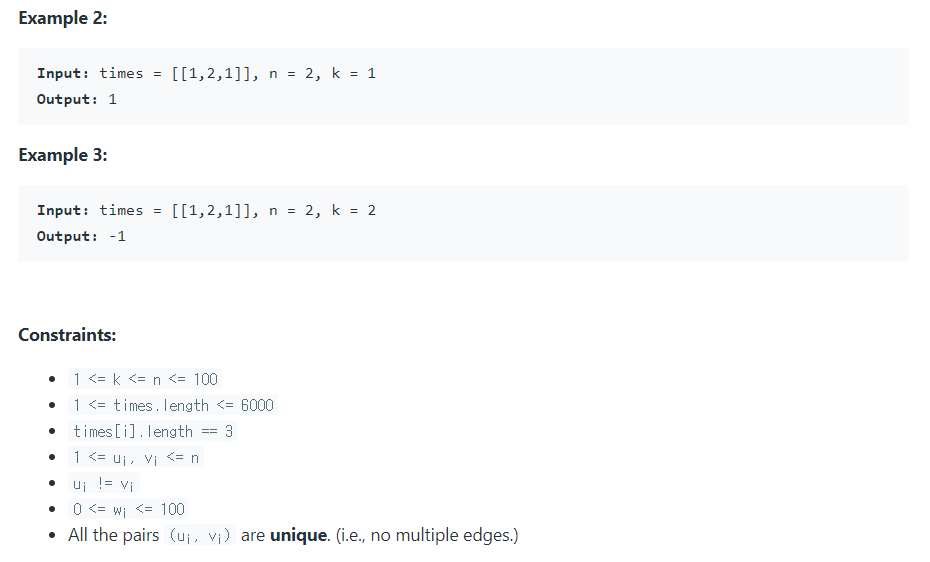
K부터 출발해 모든 노드가 신호를 받을 수 있는 시간을 계산하라.
- 불가능할 경우 -1을 리턴한다.
-
입력값 (u, v, w)는 각각 출발지, 도착지, 소요 시간으로 구성되며, 전체 노드의 개수는 N으로 입력받는다.

1. 다익스트라 알고리즘 구현
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
graph = collections.defaultdict(list)
#그래프 인접 리스트 구성
for u, v, w in times:
graph[u].append((v, w))
#큐 변수: [(소요시간, 정점)]
Q = [(0, k)]
dist = collections.defaultdict(int)
#우선순위 큐 최솟값 기준으로 정점까지 최단 경로 삽입
while Q:
time, node = heapq.heappop(Q)
if node not in dist:
dist[node] = time
for v, w in graph[node]:
alt = time + w
heapq.heappush(Q, (alt, v))
#모든 노드의 최단 경로 존재 여부 판별
if len(dist) == n:
return max(dist.values())
return -1
-
이 문제에서는 다음과 같은 2가지 사항을 반별해야 한다.
1) 모든 노드가 신호를 받는 데 걸리는 시간
-
가장 오래 걸리는 노드까지의 시간
- 즉, 가장 오래 걸리는 노드까지의 최단 시간
-
이는 다익스트라 알고리즘으로 추출할 수 있다.
2) 모든 노드에 도달할 수 있는지 여부
-
이는 모든 노드의 다익스트라 알고리즘 계산 값이 존재하는지 유무로 판별할 수 있다.
-
만약 노드가 8개인데 다익스트라 알고리즘 계산은 7개 밖에 할 수 없다면, 나머지 한 노드에는 도달할 수 없다는 의미이다.
- 이 경우 모든 노드에 도달할 수 없는 경우이므로 -1을 리턴한다.
-
- 파이썬에서 우선순위 큐를 최소 힙(Min Heap)으로 구현한 모듈인
heapq를 사용하는 형태로 구현해본다.
<우선순위 큐를 이용한 다익스트라 알고리즘 수도코드>
function Dijkstra(Graph, source):
dist[source] <- 0
create vertex priority queue Q
for each vertex v in Graph:
if v ≠ source
dist[v] <- INFINITY
prev[v] <- UNDEFINED
Q.add_with_priority(v, dist[v])
while Q is not empty:
u <- Q.extract_min()
for each neighbor v of u:
alt <- dist[u] + length(u, v)
if alt < dist[v]
dist[v] <- alt
prev[v] <- u
Q.decrease_priority(v, alt)
return dist, prev- 그래프에서 각 정점과 거리를 우선순위 큐에 삽입하는 부분
Q.add_with_priority(v, dist[v]), 그리고 우선순위 큐에서 최소 값 추출u <- Q.extract_min()을 통해서 이웃을 살펴보는for each neighbor v of u:수도코드를 확인할 수 있다.
-
실행 가능한 파이썬 코드로 구현해보자.
-
그래프부터 구성한다.
-
위키피디아 수도코드는 이미 그래프가 구성된 상태라 가정하고 입력값을 받았지만, 이 문제에서 입력값은 (u, v, w) 아이템 목록으로 구성된 리스트 형태며, 이를 키/값 구조로 조회할 수 있는 그래프 구조 (파이썬에서는 딕셔너리로 구현하는 인접 리스트)는 아니다.
-
따라서 먼저 그래프를 인접 리스트로 표현하는 딕셔너리부터 만들어준다.
-
딕셔너리 생성을 쉽게하기 위해
collections.defaultdict를 활용한다.
-
-
다음은 우선순위 큐를 위한 큐 변수를 정의한다.
-
큐 변수
Q는 '(소요시간, 정점)` 구조로 구성한다.- 즉 시작점에서 '정점'까지의 소요 시간을 담아둘 것이다.
-
초깃값은 시작점 K부터이므로, 소요 시간은 0이고, 따라서 (0, K)가 된다.
-
거리를 의미하는
dist변수는 아직 아무것도 셋팅하지 않는다.
-
-
수도코드에는 큐에
add_with_priority(),decrease_priority(),extract_min()3번의 연산을 내리도록 구현되어 있다.-
여기서
decrease_priority()가 문제다. -
이 연산은 수도코드에서 우선순위를 조정하라는 의미로 쓰였는데, 우리가 사용하는
heapq모듈은 우선순위 업데이트를 지원하지 않기 때문이다.- 우선순위를 업데이트하려면 먼저 해당되는 키를 찾아야하고 이는 결국 O(n) 시간 복잡도가 필요한 일로,
heapq모듈은 이 기능을 지원하지 않는다.
- 우선순위를 업데이트하려면 먼저 해당되는 키를 찾아야하고 이는 결국 O(n) 시간 복잡도가 필요한 일로,
-
여기서는
decrease_priority()가 필요 없도록 알고리즘을 살짝 변경해 구현해본다.
-
-
큐 순회를 시작하자마자 최솟값을 추출하는 건 수도코드와 동일하다. 그러나 바로 for each 구문으로 이웃 노드를 순회했던 수도코드와 달리, 그 작업은 잠시 뒤에 진행하고, 먼저
dist에 node의 포함 여부부터 체크한다.-
수도코드는
dist를 이미 무한대 값으로 채우고 시작했지만, 우리는dist에 아무 값도 셋팅하지 않았기 때문에 처음에는 이 값이 비어있을 것이고, 이 경우에만 힙에 푸시(Push)하는 형태로 조금 다르게 구현할 것이다.- 이렇게 하면 큐의 우선순위를 업데이트할 필요 없이 존재 유무로만 진행할 수 있으며,
dist에는 항상 최솟값이 셋팅될 것이다.
- 이렇게 하면 큐의 우선순위를 업데이트할 필요 없이 존재 유무로만 진행할 수 있으며,
-
<최단 경로를 찾아 나가는 과정 도식화>
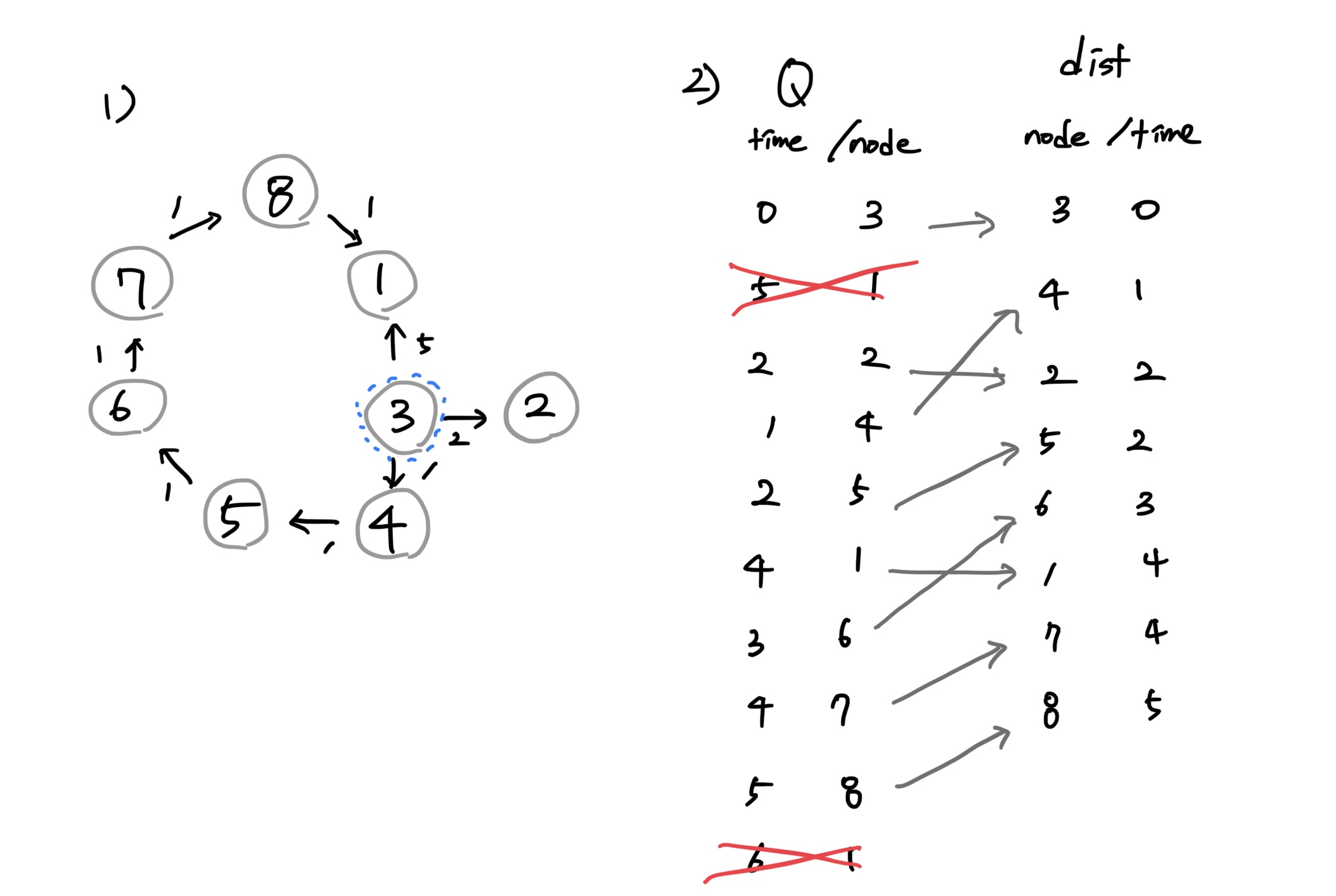
입력값 [[3,1,5], [3,2,2], [2,1,2], [3,4,1], [4,5,1], [5,6,1], [6,7,1], [7,8,1], [8,1,1]]
여기서 N = 8이고 K = 3이다.
-
1)은 입력값을 그래프로 표현한 것이다.
- 시작점인 3을 중심으로 세 방향으로 뻗어나가는 구조다.
-
2)의
Q와dist는 위에서부터 차례로, 변수에 삽입되는 순서대로 값을 나열했다.-
여기서
Q는 우선순위 큐이므로 값이 계속 쌓이다가 낮은 값부터 하나씩 추출되면서(최소 힙이다) 제거된다. -
dist에 존재하지 않는다면 바로dist의 값으로time과node의 순서가 바뀌면서 입력된다. -
이미
dist에 키가 존재한다면 그 값은 버리게 된다.dist에는 항상 최솟값부터 셋팅되기 때문에 이미 값이 존재한다면 그 값은 더 오래 걸리는 경로이기 때문이다. 따라서 이 값은 버리게 된다
-
그림의 2)에서는 [5,1], [6,1] 두 값이 버려지게 된다.
-
-
실제로 노드 1은 3->2->1 순서로 방문하면 소요 시간 4에 도달할 수 있으며, 이후에 삽입되려고 하는 5와 6은 모두 이보다 더 오래 걸리므로 모두 버린다.
- 가장 먼저 입력되었던 경로가 최단 경로이며, 이후에 삽입되는 경로는 이보다 오래걸린다.
-
마지막으로 모든 노드에 도달할 수 있는지 여부를 판별한다.
-
dist딕셔너리의 키 개수가N과 동일한지 체크한다.-
전체 노드 개수만큼이 모두
dist에 있다면 모든 노드의 최단 경로를 구했다는 의미이고, 이는 모두 시작점에 도달이 가능하다는 의미이기도 하다. -
만약 노드 개수가 하나라도 모자란다면 그 노드는 시작점에서 도달할 수 없다는 뜻이며, 앞서 2가지 판별 조건 중 두 번째 조건을 만족할 수 없기 때문에 -1을 리턴한다.
- 모든 노드가 신호를 받을 수 없기 때문
-
-
